题目:

分析:
对于一个点i来说,它能与j连边仅当两个点的距离>=权值之和,画图抽象出来就是这样:
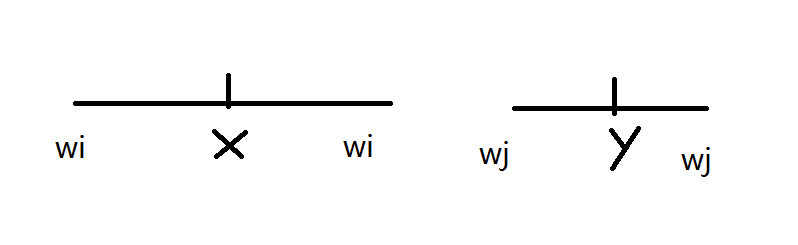
将每一点都抽象成一个线段,那么不相交的线段间一定会有连边,问题就转化成了->求最多的线段覆盖。
线段覆盖求法: 贪心。将线段按右端点排序,从左往右依次选取。
正确性:每次选右端点尽量靠左的,后面的选择余地就越多。
注意:当右端点相同的时候,要按左端点从小到大排序,因为如果出现左右端点相同的线段,要接着与它右端点相同的点选。
#include<bits/stdc++.h> using namespace std; #define N 200005 struct node{ int l,r; }e[N]; bool cmp(const node &a,const node &b) { if(a.r==b.r) return a.l<b.l;//如果有空节点 要优先选非空区间 然后后面接一个空区间 这要为答案贡献 1 return a.r<b.r; } int main() { freopen("clique.in","r",stdin); freopen("clique.out","w",stdout); int n,a,b; scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d%d",&a,&b),e[i].l=a-b,e[i].r=a+b; sort(e+1,e+1+n,cmp); int mx=e[1].r,ans=1; for(int i=2;i<=n;i++){ if(e[i].l>=mx) mx=e[i].r,ans++; } printf("%d ",ans); return 0; } /* 4 2 3 3 1 6 1 0 0 6 1 3 5 1 7 1 10 0 12 1 13 6 */