一、问题描述
①在箱子装载问题中,有若干个容量为c的箱子和n个待装载入箱子中的物品。物品i需占是s[i]个单元(0<s[i]<=c)。所谓成功装载(feasible packing),是指能把所有物品都装入箱子而不溢出,而最优装载(optimal packing)是指使用了最少箱子的成功装载。对于箱子装载问题,有4种流行的求解算法。
②基本要求:
->n依次取100,200,500,1000,比较以上四种方法(在时间上和所用箱子的数量上)的性能。
->FF,FFD方法使用竞赛树结构,BF,BFD使用二叉搜索树结构。
二、需求描述
1.4种流行的求解算法:
<1>最先匹配法(FF):物品按1,2...,n的顺序装入箱子。假设箱子从左至右排列,每一物品i放入可盛载它的最左箱子。
<2>最先匹配递减法(FFD):方法与FF类似,区别在于各物品首先按容量递减的次序排列,即对于1<=i<n,有s[i]>=s[i+1].
<3>最优匹配法(BF):设c[j]为箱子j的可用容量,初始时,所有箱子的可负载容量为c。物品i放入具有最小c且容量大于s[i]的箱子中。
<4>最优匹配递减法(BFD):方法与BF相似,区别在于各物品首先按容量递减的次序排列,即对于1<=i<n,有s[i]>=s[i+1].
2.输入要求:
①第一种输入方式:n在程序中固定读入100,200,500,1000个数,这些数预先在文本中手动输入为固定的无序正整数。
②第二种输入方式:n为程序运行后,人为输入的数n,并且生成n个随机数,用作程序所需要测试的物品大小数。
3.输出要求:
输出的要求为:直观的分析排列出在不同的箱子数量、不同的物品数量以及不同的物品大小的情况下,上述四种方法在时间上和所用的箱子的数量上的不同。
比较四种方法的性能。
4.界面设计:
使用的是程序运行控制台输出,没有使用图形化界面。
界面设计如图:
①第一种输入方式:

②第二种输入方式

5.测试设计:
使用第一种方式输入数据:首先分别将100,200,500,1000个数据输入到一个文本文件中,然后在程序中使用读取文件的方法将文本文件的数据当做程序的测试数据,进行测试实验。
读取文件的方法为:

使用的测试数据为:
①100个数据

②200个数据
③500个数据
④1000个数据
数据就是大同小异啦,自己建立txt文件输入数据就好
三、设计
3.1结构设计
①对于最先匹配法(FF)和最先匹配递减法(FFD)方法使用了竞赛树结构。
----->对于竞赛树的结构设计
*T[i]代表胜者
*P[I]代表参赛者
*当外部节点为n,则内部节点为n-1
*最底层最左端的内部节点编号为s
*最底层外部节点个数lowext=2(n-s)
*最底层内部节点个数为n-s
*令offset=2*s-1,对任何一个外部节点P[I],可根据公式得出其父节点
(i+offset)/2 i<=lowext
p=
(i-lowext+n-1)/2 i>lowext
----->使用竞赛树对于上述方法的具体实现
*将竞赛树的外部节点当做容量为c的箱子,构建赢者树,先从左子树开始查找判断是否可以容纳物品,逐步向下寻找,因为内部节点返回的是外部节点的胜者(这里规定为箱子容量更大的一个作为胜者)即箱子号,便可以找到可以使用的箱子(即对应外部节点),在使用箱子后,箱子的容量减去物品大小,并重构赢者树,形成新的胜者。
*初始化时,对所有n个箱子,bin [i] .unused Capacity=bin Capacity。
bin [i] 作为选用,对最大赢者树进行初始化。
*FF和FFD利用了数据类型bintype,该类型只有一个数据成员,unused Capacity 并重载了操作符<=,使表达式x<=y的值为真,当且仅当x.unused Capacity>=y.unused Capacity。
*FF和FFD假定,除非右边选手大于左边选手,否则左边选手为胜者。
*竞赛树是用数组表示的完全二叉树,它能按照数组的下标乘2或加1方式从上向下移动。
②对于最优匹配法(BF)和最优匹配递减法(BFD)使用了二叉搜索树结构。
----->对于二叉搜索树的结构设计
*对于二叉搜索树由链表描述,因为二叉搜索树的元素和形状随操作而改变,从链式描述二叉树类派生
*使用带有重复关键字的二叉搜索树能在O(nlogn)时间内实现最优匹配法。
*在根节点的左子树中,元素的关键字(如果有的话)都小于根节点的关键字。
*在根节点的右子树中,元素的关键字(如果有的话)都大于根节点的关键字。
*根节点的左、右子树也都是二叉搜索树。
----->使用二叉搜索树对于上述方法的具体实现
*在实现最优匹配法时,搜索树的每个元素代表一个正在使用且剩余容量不为0的箱子
*因为箱子不同,但剩余容量可能相同,可以用一棵带有重复关键字的二叉搜索树来描述箱子,每个箱子的剩余容量作为节点的关键字。
*节点的内部值为箱子的剩余容量,节点外部是箱子的名称。
*从根节点开始(左小右大),右子树均可以,则先进入左子树进行查找,若满足可装载,则成为候选者,再进入左子树,若不满足则进入其右子树一直往下找,直到没有子树,则没有更好的候选者,所以箱子i即是要找的箱子。
*当物品i找到最匹配箱子后,可将它从搜索树中删除,将其剩余容量减去s[i]再将它重新插入树中(除非它的剩余容量为0),若没有找到最匹配的箱子,则启用一个新箱子。
*对于二叉搜索树的元素类型是一个偶对pair<const K,E>,其中K是关键字类型,E是相应的元素的数据类型。
3.2类设计(共设计了5个类来完成整个程序)
①竞赛书实例
{ 实例:
完全二叉树,每个节点指向比赛胜者,外部节点表示参赛者
操作:
Initialize(a);为数组a的参赛者初始化胜者树
Winner();返回胜者
Replay(i);在参赛者i改变之后重赛
}
抽象类Winner Tree
1 template<class T> 2 class winnerTree 3 { 4 public: 5 virtual ~winnerTree() {} 6 virtual void initialize(T *thePlayer, int theNumberOfPlayers) = 0; 7 //用参赛者数组建立赢者树 8 virtual int winner() const = 0; 9 //返回赢者的索引 10 virtual void rePlay(int thePLayer) = 0; 11 //根据参赛真的改变重新构造赢者树 12 };
②最大赢者树类继承竞赛树类实现其中的抽象方法,并定义了使用的变量

1 template<class T> 2 class completeWinnerTree : public winnerTree<T> 3 { 4 public: 5 completeWinnerTree(T *thePlayer, int theNumberOfPlayers) 6 { 7 tree = NULL; 8 initialize(thePlayer, theNumberOfPlayers); 9 } 10 ~completeWinnerTree() {delete [] tree;} 11 void initialize(T*, int); 12 int winner() const 13 {return tree[1];} 14 int winner(int i) const 15 {return (i < numberOfPlayers) ? tree[i] : 0;}// 返回节点i的赢者 16 void rePlay(int); 17 void output() const; 18 private: 19 int lowExt; // 最底层外部结点个数 20 int offset; // 2^log(n-1) - 1 21 int *tree; //赢者树的数组 22 int numberOfPlayers; 23 T *player; //参赛者的数组 24 void play(int, int, int); 25 };
③定义二叉树类

1 template<class T> 2 class binaryTree 3 { 4 public: 5 virtual ~binaryTree() {} 6 virtual bool empty() const = 0; 7 virtual int size() const = 0; 8 virtual void preOrder(void (*) (T *)) = 0; 9 // 前序遍历输出二叉树 10 virtual void inOrder(void (*) (T *)) = 0; 11 virtual void postOrder(void (*) (T *)) = 0; 12 virtual void levelOrder(void (*) (T *)) = 0; 13 protected: 14 int treeSize; 15 };
④引用了字典类,用于实现元素类型为偶对pair<const K,E>

1 template<class K, class E> 2 class dictionary 3 { 4 public: 5 virtual ~dictionary() {} 6 virtual bool empty() const = 0; 7 //当字典为空时,返回ture 8 virtual int size() const = 0; 9 //返回字典中数对的数量 10 virtual pair<const K, E>* find(const K&) const = 0; 11 //返回字典中匹配的数对 12 virtual void erase(const K&) = 0; 13 //删除对应数对 14 virtual void insert(const pair<const K, E>&) = 0; 15 //在字典中插入新数对 16 };
⑤二叉搜索树继承字典类,实现字典类的多有抽象方法,并由链式二叉树派生

1 template<class K, class E> 2 class binarySearchTree : public bsTree<K,E> 3 { 4 public: 5 // 实现字典类的方法 6 bool empty() const {return treeSize == 0;} 7 int size() const {return treeSize;} 8 pair<const K, E>* find(const K& theKey) const; 9 void insert(const pair<const K, E>& thePair); 10 void erase(const K& theKey); 11 pair<const K, E>* findGE(const K& theKey) const; 12 void ascend(){} 13 binarySearchTree() {root = NULL; treeSize = 0;} 14 15 protected: 16 binaryTreeNode<pair<const K, E>> *root; // 指向根的指针 17 int treeSize; // 树的节点个数 18 };
⑥在main函数中,加入上述头文件
使用switch case语句构成方法的选择。
3.3函数设计及分析
对于方法的设计都存放在player.h头文件中。
①对于最先匹配法(FF)方法的设计
首先声明一个箱子类型,将每个箱子的大小初始化为从键盘中接收到的数据,然后用初始化后的箱子构建竞赛树。
然后将物品依次装入箱子中,先从根的左孩子开始搜索,判断左孩子中的剩余容量是否装的下物品,即判断箱子剩余容量的大小与物品的大小。
设置一个整数变量binTouse作为要使用的箱子,binTouse的值是内部节点孩子的比赛中的获胜者,将物品装入该箱子中,然后更新箱子的容量,用箱子容量减去物品大小得到新的箱子容量,之后重新构造赢者树,进行下一个物品的装入。
之后用新的箱子剩余容量与之后所有物品的大小进行比较,用于统计箱子的使用数量,当之后的物品大小都大于箱子的新剩余容量,确认这个箱子无法在装入物品,箱子使用数量加1;若至少有一个物品大小小于箱子的新剩余容量,确认这个箱子在之后还能被再次使用,箱子使用数量不改变。
②对于最先匹配递减法(FFD)方法的设计
首先对于接收进来的箱子大小进行递减排序,然后方法主体与最先匹配法(FF)方法相同,使用①所用的步骤进行箱子装箱的实现。
③对于最优匹配法(BF)方法的设计
首先声明一个二叉搜索树类的箱子容量树,每个箱子声明为一个数对类型,first是箱子容量,second是箱子的序号。然后进行将物品逐个装箱,将物品i装箱,并且寻找最匹配的箱子,使用在二叉搜索树类中定义的方法findGE(),返回目前找到的元素,其关键字是不小于thekey的最小关键字。
当没有足够大的箱子时启用一个新箱子,若箱子容量可以装下物品,则在装入物品后,将该箱子节点先从箱子容量树中删除,并用箱子的剩余容量减去物品的大小,然后将改变后的箱子作为新节点重新插入箱子容量树中。
之后用新的箱子剩余容量与之后所有物品的大小进行比较,用于统计箱子的使用数量,当之后的物品大小都大于箱子的新剩余容量,确认这个箱子无法在装入物品,箱子使用数量加1;若至少有一个物品大小小于箱子的新剩余容量,确认这个箱子在之后还能被再次使用,箱子使用数量不改变。
④对于最优匹配递减法(BFD)方法的设计
首先对于接收进来的箱子大小进行递减排序,然后方法主体与最有匹配法(BF)方法相同,使用③所用的步骤进行箱子装箱的实现。
四、测试结果
①第一种输入方式,即n在程序中固定读入100,200,500,1000个数,这些数预先在文本中手动输入为固定的无序正整数。
----->首先根据菜单提示进行操作

----->分别使用100、200、500、1000个物品的数据进行测试输出结果

②使用第二种输入方法,即人为输入的数n,并且生成n个随机数,用作程序所需要测试的物品大小数。
----->首先先输入物品的数目

----->根据菜单提示进行操作

----->输出结果
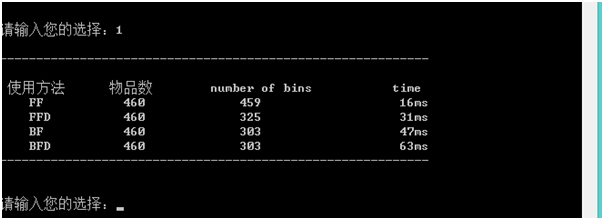
五、分析与探讨
通过实验结果,可以看出使用不同的方法会对同一个问题有不一样的性能,在时间使用上,和箱子数量的使用上都有差别。
在使用箱子数量上,可以画出不同方法的比较图

对于不同的问题,每种方法的适用范围也不同,并不能武断的判定哪种方法较好,哪种方法不好。
对于程序的改进,使用了两种输入方式,通过菜单栏的选择来选择不同的测试方式和实现的功能,可以人为的输入需要测试的数据数量,也可以使用程序中固定的数据进行进一步的测试。
该课程设计内容主要是利用数据结构中的竞赛树和二叉搜索树来实现方法,也从此次实验中,我学到了更多对数据结构应用的知识,实用数据结构可以使程序的性能得到提升,占用的资源也会合理。
整理大二时写的数据结构课设代码,之中还有很多问题,待修改后再放上来。
整理于2017年4月26日
