一、冒泡算法
1、将两个变量的值互换
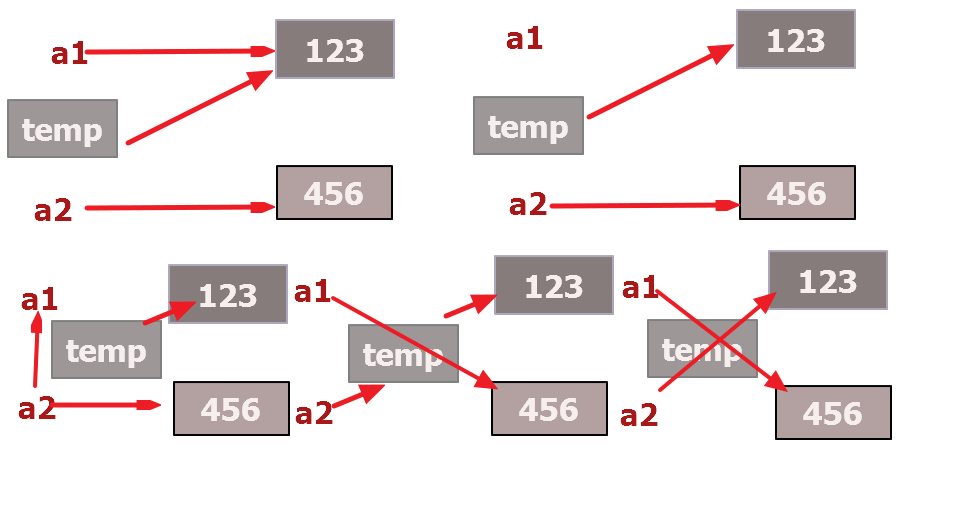
a1 = 123 a2 = 456 #要想将a1与a2的值进行位置互换需要借助一个中间变量(temp) temp = a1#将a1的值赋值给temp(temp=123) a1 = a2 #将a2的值赋值给a1,此时的a1=456 a2 = temp#将temp的值赋值给a2,此时a2=123 print(a1) print(a2)
结果:
a1 = 456 a2 = 123
2、冒泡算法
li = [33,2,10,1]
for j in range(1,len(li)):
for i in range(len(li) - j):
# i = 0 1 2 3
# li[0] 1 2 3
# li[1] 2 3 4 长度等于3这里到了4已经超出范围所以len(li)要减 1
if li[i] > li[i + 1]:
temp = li[i]
li[i] = li[i + 1]
li[i + 1] = temp
print(li)
注:内层的for循环是为了找出列表中的最大值放到最后,外层的for循环是为了把除了最大值之外的其他值进行排序,最后把列表的顺序变成了由小到大的顺序。
二、递归算法
- 在函数的内部可以调用其它函数,如果一个函数在其内部调用自身,则这个函数就是递归函数。
- 在我们使用递归函数时,必须有一个明确的递归结束条件(递归出口)。
递归算法一般用于解决三类问题
- 数据的定义是按递归定义的(Fibonacci函数)
- 问题的解决办法是按照递归算法
- 数据的结构形式是按递归定义的
递归的缺点:递归算法的解题的运行效率较低,在递归调用的过程中,系统为每一层的返回点、局部量等开辟了栈来存储,递归的次数过多容易造成栈的溢出
这里用斐波那契数列来演示递归:
斐波那契数列:
0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765
#0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987
li = []
def f1(depth,a1,a2):
#为了更好的观察程序的每一步斐波那契数列的动向,我们定义了一个depth来观察
#斐波那契数列从0开始
li.append(a1)#将每一次循环的a1放到li列表中这就是要找的斐波那契数列
print("这是第%s次循环:"%depth,a1,a2)#打印出循环的次数、a1、a2
if depth == 5:#当斐波那契数列的深度到5的时候将li列表返回给调用者
return li
a3 = a1 + a2
r = f1(depth+1, a2, a3)#用变量r来接收f1函数的值
return r
ret = f1(1,0,1)#执行函数f1,这里也是函数的入口
print(ret)打印函数执行的结果
结果:
这是第1次循环: 0 1 这是第2次循环: 1 1 这是第3次循环: 1 2 这是第4次循环: 2 3 这是第5次循环: 3 5 [0, 1, 1, 2, 3]
这里我们来看一下递归执行过程中的动态展示:

执行流程图示:

三、装饰器
装饰器实际上就是函数。
装饰器的语法:
装饰器以@开头,接着是装饰器函数的名字和可选的参数,紧跟着装饰器声明的是被修饰的函数和装饰函数的可选参数 。
Demo:
@outer
1、执行outer函数,将index作为参数传递
2、将outer的返回值,重新赋值给index
def outer(func):
def inner(a1,a2):
print("123")
ret = func(a1,a2)
print("456")
return ret
return inner
@outer
def index(a1,a2):
print("费劲")
return a1 + a2
m = index(1,2)
print(m)
这个装饰器的执行流程:
1、装饰器的执行流程代码从上到下执行
2、将def outer(func)函数整体读取到内存中,不做任何处理
3、遇到@outer
*执行outer函数,将index作为参数传递
*将outer函数的返回值重新赋值给index
4、将被装饰的函数作为参数传递给outer函数==>def outer()
5、读到def inner(a1,a2),inner函数中并没有任何对inner的调用,所以inner函数的内部并不执行任何操作(直接放到内存当中)
6、执行return inner操作将outer的返回值从新赋值给index(此时的index函数,相当于inner函数)
7、此时执行def inner(a1,a2)函数
8、打印123
9、执行ret = func(a1,a2)这里的func相当于原来的index函数,根据@的特性这里要执行最初的index函数将"费劲"打印出来
10、将return a1 + a2返回给ret
11、执行打印456
12、将ret返回给他的调用者func也就是index并打印出来m = 3
动态展示装饰器的执行过程:

多个装饰器
def outer_0(func):
def inner(*arg,**kwargs):
print("3.5")
ret = func(*arg,**kwargs)
print("789")
return ret
return inner
def outer(func):
def inner(*arg,**kwargs):
print("123")
ret = func(*arg,**kwargs)
print("456")
return ret
return inner
@outer_0
@outer
def index(a1,a2):
print("死磕到底--德玛西亚")
return a1 + a2
m = index(1,2)
print(m)
执行流程:
两个装饰器装饰同一个函数 装饰器的作用: *执行装饰函数,将被装饰的函数作为参数传递 *将装饰器函数的返回值,重新复制给被装饰的函数 1.将def outer_0():放到内存当中 2.将def outer():放到内存当中 3.遇到第一个装饰器outer_0 4.由于这里是两个装饰器在一起所以程序会继续寻找下一个装饰器outer *执行outer函数 *将outer函数内部的inner函数读取到内存当中,由于inner内部没有对函数的调用这个函数不进行任何操作 *执行outer_0函数 *将outer_0函数读取到内存,继续读取outer_0内部的inner函数,inner内部没有对函数的调用所以没有任何操作 *将函数的返回值inner重新赋值给index函数 (这里就相当于对函数内部的inner函数重新命名为index函数) outer_0在嘴上面先赋值给他,执行其内部的inner *打印3.5 *执行ret = func() 这里的func函数相当于outer函数的内层函数inner *打印123 *执行outer函数里的ret = func() *到@outer_0装饰器 *打印“死磕到底--德玛西亚” *打印outer函数的456 *打印789 将返回值ret返回给调用者m
执行流程的动态展示:
