深度学习中的各种tricks_2.0_maxout
2017/11/18 - Saturday - 第一次修改
[ 用于整理遇到的NN设计中使用的不同结构和trick的原理与实现 ]
maxout (最大输出激活函数)
2017/11/18
以下内容主要根据 ref.2 中的 slide 以及 ref.1 中的 Abstract 和 Introduction。
maxout 简介
maxout 得名时因为它的 out put 是输入集合中的 max ,而且一般和dropout一起使用。论文作者提出 maxout 的本意就是设计一个 model 让它可以 leverage 作为 model averaging tech 的 dropout。而且论文作者经验性的证明了 maxout 和 dropout 一起可以对于优化和 model averaging 有效果。
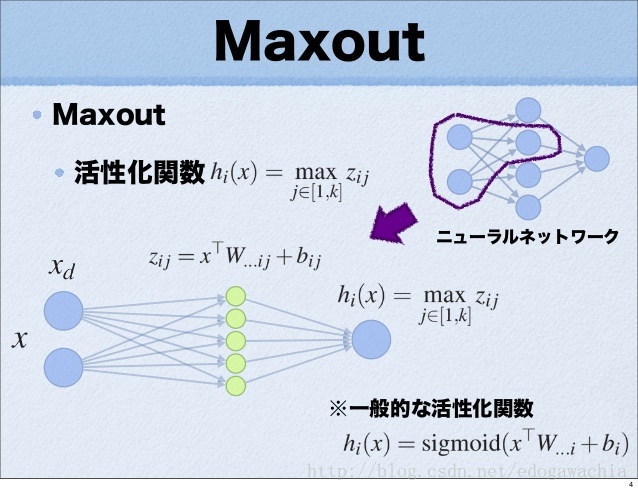
maxout 作为新的激活函数
maxout 可以被视为一种新的激活函数。如图所示,一般的NN都是先对输入(x)进行加权求和(得到z)再输入进一个非线性函数h中,输出即为激活函数的值(h(z))。而 maxout 不同,它去掉了后面的非线性函数,并且对于后一层的每个值,都相当于在前面加了一个 hidden layer,而且时没有 activation 的 hidden layer , 而且从 hidden layer 到后一层的值之间并不是加权求和,而是取 max 。(这样看来其实也不能算作 hidden layer … 只是可能几何结构上有些类似,更应该看作 hidden layer 中的每一个 node 都相当于一个可能的 output ,如果只看某一种可能性的话,模型就退化成普通的 FC 层了。而最后的输出只不过是在所有可能的输出中取最大值)
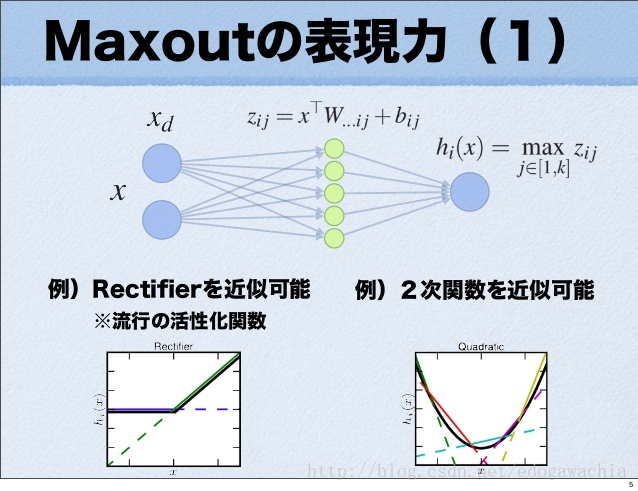
maxout 的表达能力
对于每一个 x–>z 的映射,都是一个线性函数,因此最后取 max 实际上是对所有可能的线性函数取最大,因此会得到一个分段线性的激活函数,而且由于是取max,则分段函数必然是凸的,而且由于我们认为激活函数是凸的,那么如果给定足够多的分段,那么原则上 maxout 是可以拟合任意的激活函数的。下面展示的就是 maxout 拟合 ReLu 和 二次函数 的情形
下面是定理,用来说明 maxout 的表达能力,首先,定理一说明,只要隐节点足够多,任何凸函数都可以用 maxout 来近似,而后说明如果 f 和 g 时凸的,那么任意函数都能由 f - g 来近似。所以得到定理二,即 maxout 相减可以拟合任意函数。 所以多层的 maxout 具有很强的表现力。
由于 maxout 是 PWL (Piecewise Linear) 的,因此可以用BP更新。
reference:
- Goodfellow I J, Wardefarley D, Mirza M, et al. Maxout Networks[J]. Computer Science, 2013:1319-1327.
- 論文紹介 Maxout Network 斎藤淳哉