KMP字符串匹配算法
任务概述
字符串匹配任务,即从一个主串中找到与模式串相同的部分,并且返回它的位置,可以通过遍历的方法暴力实现,成为BF算法,即 brute force ,暴力算法。暴力算法是这样实现的 :如果主串中的一部分已经匹配好了模式串中的一部分,那么当下一个char不匹配的时候,就要从头来过,也就是把主串和模式串对齐的位置,也就是模式串的第一个char的位置往右移动一格,然后对齐,重新比较。这样的话,对于主串中比较的那个指针来说,实际上有个回溯的过程。所谓的KMP算法是对暴力求解的一种改进。KMP的基本想法是,既然我们已经匹配成功了很多字符,那么即使后面的失配,前面得到的信息还是有用的,它的用途就是让我们在把模式串往右移动的时候可以避免错过匹配点地较大幅度的移动。
KMP算法得名于Donald Knuth、Vaughan Pratt、James H. Morris三个人。暴力匹配的最坏的时间复杂度为O(m×n),其中m和n分别是子串和主串的长度,而KMP可以做到O(m+n)。比如说,下图这种情况,

已经匹配了四个了,但是最后一个失配,如果按照暴力算法,则要从主串的5号位置开始,把主串的5号与模式串的0号对齐,然后依次向后比较。而我们发现,实际上并无需如此,因为前面的四个已经匹配好了,有没有可能直接吧子串右移一定的数量,而不是仅仅移动一格,但是还能保证我们的移动没有错过可能匹配上的情况呢?这就引出了所谓前缀和后缀的概念。
前缀后缀最长公共子串长度
首先,介绍概念。比如对于一个序列:
excited
它的前缀包括:e, ex, exc, exci, excit, excite
它的后缀包括:d, ed, ted, ited, cited, xcited
当然这个词的前缀和后缀没有公共的元素。另举一个栗子:
excitex 这个串里面,公共的前后缀就是ex,长度为2,而像这个:
eexee 这个里面,前缀e和后缀e相同,ee和ee相同,eex和xee不同了,所以最长的长度为2
为什么要讨论一个串中的前后缀有没有相同呢?原因如下:由于当我们匹配了一部分的时候,实际上我们知道子串中的那一部分是和主串中的对应位置一样的。那么我们希望进行一个预处理,即我们假设在某一个位置失配了,那么前面匹配的那部分,也就是子串的子串中,前后缀公共长度最长是多少我们可以预先计算并记录下来。记录这个值的作用在于,比如上图的情况,abab,这个值为2,那么我们就可以直接用主串的8号和子串的2号相匹配,如下图:
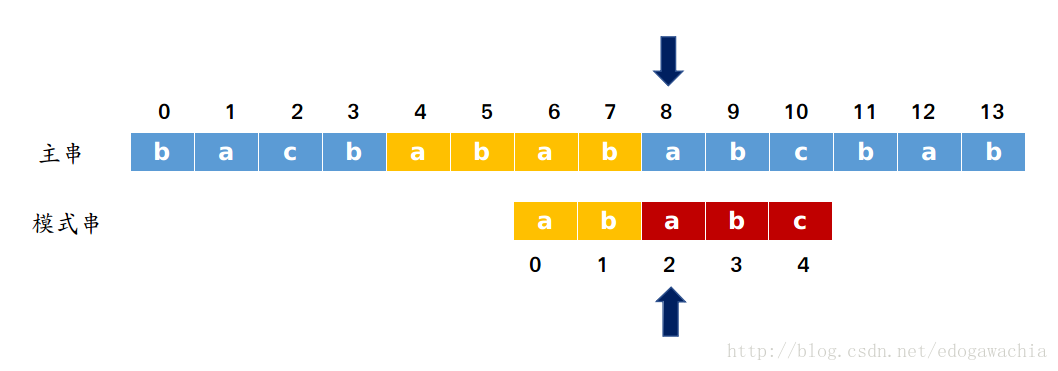
原因很显然,在这一段里,我们跳过了模式串头上的两个元素,因为我们知道,主串中对应位置和模式串中的abab是一样的,而模式串中前缀和后缀的两位也是一样的,那么主串中的6,7号位置也就是和模式串中的前两位是一样的。所以头两个已经匹配好了,直接从第三个开始匹配就行。那有个疑问,这样一来没有错过其他可能的匹配点吗?答案是没有,因为假如中间有其他的,那么子串应该有更长的前缀和刚才已经匹配过的主串(绿色部分)的后几位匹配,而主串的后几位也就是已匹配的子串的后几位,那么换句话说,子串应该有更长的前缀和自己的后缀相匹配。这是不可能的,因为我们移动的位置是最长公共前后缀的后一位,我们当前的子串上的指针之前的长度(即ab)已经是最长了。
由上可知,如果我们预先计算好模式串中每个点之前的子串的最大公共前后缀长度,并把它作为一个和模式串等长的数组存起来,那么之后就会更快的匹配。这个数组通常叫做next数组,因为它表征着在该位置失配后下一个需要匹配的模式串的位置。
next数组计算
先看一个next数组的样子:
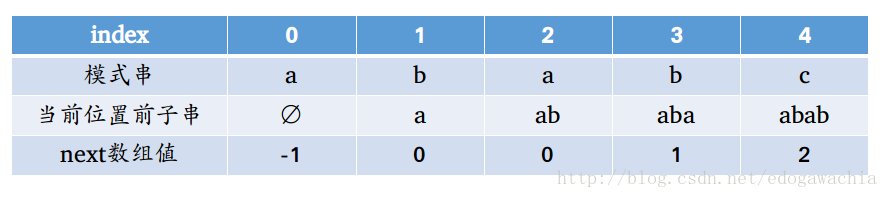
可以看出,next数组值是通过当前位置前子串的最长前后缀匹配长度计算的,第0号位置由于没有前子串,所以next数组值设定为-1,这是为了之后编程的方便。(所谓方便是指,假如在中间,非index=0的位置失配,那么i不需要移动,j跳转到next[j]继续匹配即可,根据next数组的定义这很显然。但是如果第一位就失配了,那么如果i不移动,j调到next[j],也就是next[0],假如还是0的话,则就永远不匹配,死循环。因此我们要让i在这种情况下,强行移动一格,将next[0]设为-1,然后判断 j==-1 的时候直接进入右移,即 i++,j++,那么j变成了0,指向了模式串开头,i往后移动了一格,美滋滋~)
而next数组的计算可以看做也是一个字符串模式匹配问题,其中主串就是整个模式串,子串是每一个位置的前子串。这样的好处就是,在计算后面的next数组值时可以利用到前面的已经计算好的next值。算法如下:
#!/usr/bin/env python2
# -*- coding: utf-8 -*-
"""
Created on Sat Feb 3 12:03:10 2018
@author: chia
"""
import numpy as np
def GetNextArray(modestr):
# initialization
NextArray = np.zeros(shape=(len(modestr),),dtype='int32')
NextArray[0] = -1
i = 0
j = -1
# while not finish whole modestr
while i < len(modestr)-1:
if j == -1 or modestr[i] == modestr[j]:
# if first element of substring or match, check next
i += 1
j += 1
NextArray[i] = j
else:
# not match, jump to next j
j = NextArray[j]
# in the outer loop, j == -1 is a trivial condition
return NextArray测试一下:
GetNextArray('ababc')
Out[96]: array([-1, 0, 0, 1, 2], dtype=int32)和前面的结果一致。
有了next数组,再用KMP算法,代码如下:
def KMP_Algorithm(mainstr, modestr, NextArray):
i, j = 0, 0
# while not finish
while i < len(mainstr) and j < len(modestr):
# if first of modestr or match, check next
if j == -1 or mainstr[i] == modestr[j]:
i += 1
j += 1
else:
# if not match jump to next possible location of modestr
j = NextArray[j]
if j == len(modestr):
return i - len(modestr)
else:
return -1用上面的栗子测试,结果为:
KMP_Algorithm('bacbabababcbab','ababc',GetNextArray('ababc'))
Out[105]: 6结果正确~
从上面的程序可以看出,指示主串的i是只增不减的,因此没有回溯,因此对于从外设输入的大数据有效,因为无需回头重读,一遍扫描即可。另外,将子串理解为右移一段距离不如直接理解成从某个点继续匹配,这样next数组的意义就很明显了~
THE END
2018/02/03 15:39 pm
让时间停着,想把话说完。 ——音乐人,陈粒