题意概述:n本书,在桌子边缘堆放,求最长长度。
首先……我们需要一点初中物理知识来推一下规律。
下图是一本书的情况,一本书时书伸出1/2处于临界状态,显然。
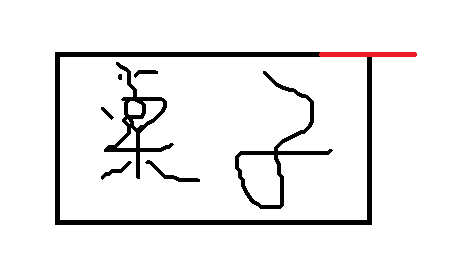
两本书时,把两本书看作整体,则有该物体的重心位于两本书的中间。
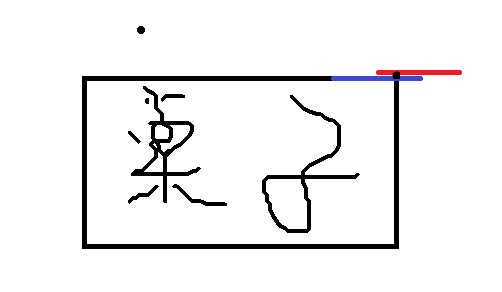 (黑点为重心)
(黑点为重心)
三本书时
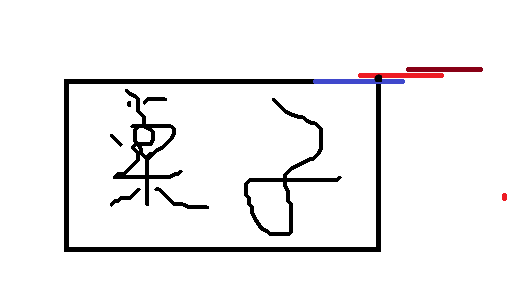
这时候我这种物理不好的蒟蒻就已经目测不出来了。不过列方程很容易可以得到重心位于最下面那本书靠近右端的六等分点。
1/2->1/4->1/6。好像有什么规律……
考虑大胆猜测不用证明,此时,题目就已经变为了求 Σ1/2i 的值了。
这个东西显然可以O(n)计算。
然而1e18的数据范围显然不允许O(n)的复杂度。
那咋整啊??神仙题啊??
我暂时还没有想到logn计算这个数列的方法。但是我们可以把数列整体*2来看。
数列变为 Σ1/i
是不是非常熟悉的调和级数?拿出调和级数求和公式最终结果除2,这题就做完了。