一、思路
假设有8个数字未被排序。
默认第一位数为已排序数字a,从剩余的7个未排序数字中拿出第一个数b,b与a进行比较,如果b小于a,则将b插入到a位置前边。
二、案例分析
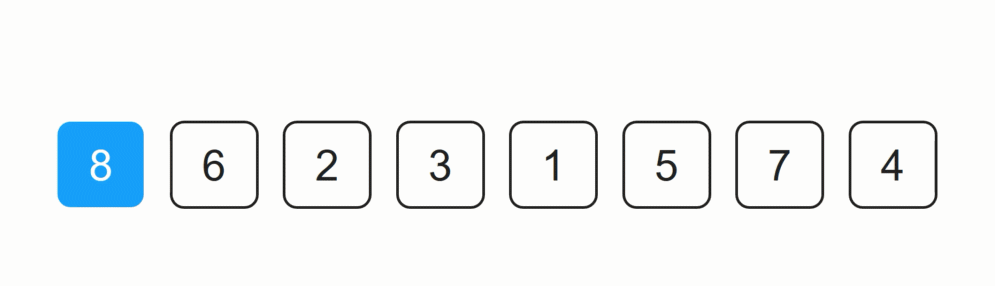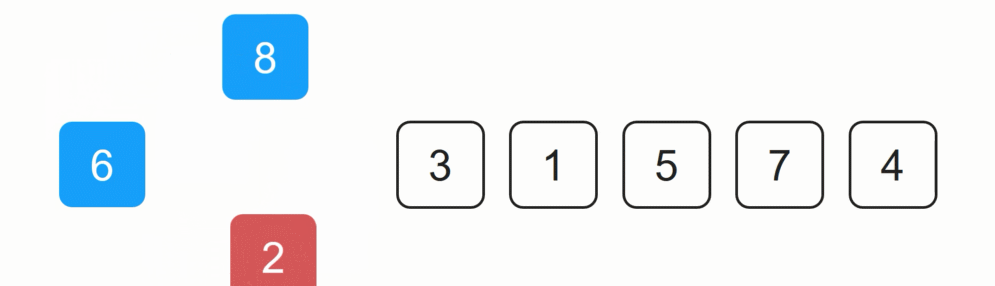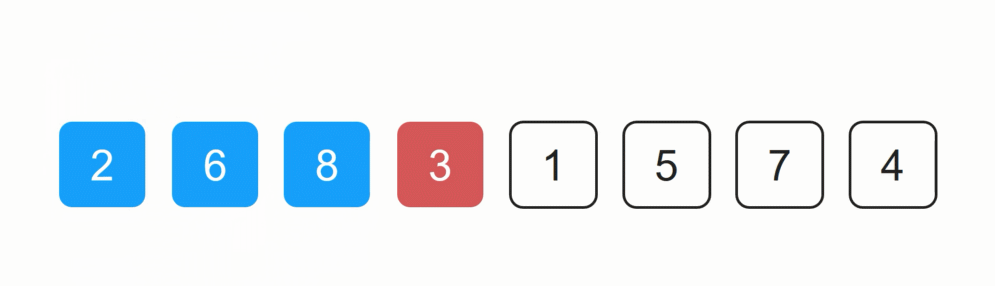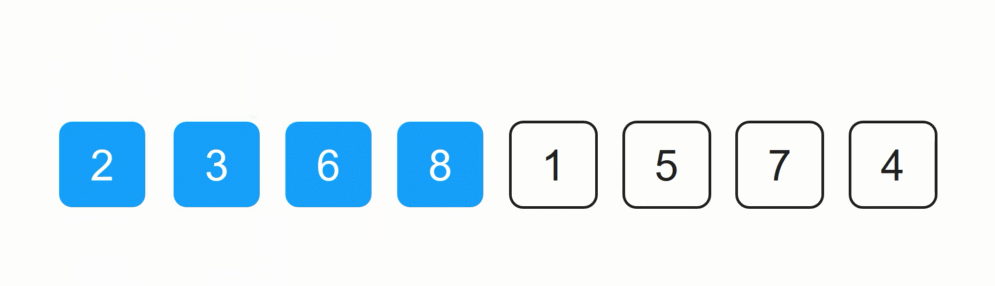
待排序数据:8 6 2 3 1 5 7 4
第一轮排序:
默认数字8已排序,剩余7个未排序数字中,数字6为未排序集合中的第一个数字,6与8进行比较大小。6小于8,因此6插入到8前边,得到如下结果:
6 8 2 3 1 5 7 4
前2个数字已经排序,剩余6个数字未排序。
第二轮排序:
剩余6个未排序数字中,数字2为未排序集合中的第一个数字,2与8进行比较大小,2小于8,因此2插入到8前边,得到如下结果:
6 2 8 3 1 5 7 4
2前边还有一个已排序的数字,2与6进行比较大小,2小于6,因此2插入到6的前边,得到如下结果:
2 6 8 3 1 5 7 4
前3个数字已经排序,剩余5个数字未排序。
......
三、编码
public class InsertionSort {
// 我们的算法类不允许产生任何实例
private InsertionSort() {
}
public static void sort(int[] arr) {
int n = arr.length;
for (int i = 1; i < n; i++) {
// 寻找元素arr[i]合适的插入位置
// 写法1
// for (int j = i; j > 0; j--) {
// if (arr[j] < arr[j - 1]) {
// swap(arr, j, j - 1);
// } else {
// break;
// }
//
// }
// 写法2
for (int j = i; j > 0 && arr[j] < arr[j - 1]; j--) {
swap(arr, j, j - 1);
}
}
}
private static void swap(int[] arr, int i, int j) {
int t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
// 测试InsertionSort
public static void main(String[] args) {
int[] arr = { 8, 6, 2, 3, 1, 5, 7, 4 };
InsertionSort.sort(arr);
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]);
System.out.print(' ');
}
System.out.println();
}
}
四、优化思路
上述算法思路中,第N轮排序,至多要进行N次数据的位置交换(swap方法中3个赋值操作),这个过程非常耗时,因此需要优化。
优化思路:
假设有8个数字未被排序。
默认第一位数为已排序数字a,从剩余的7个未排序数字中将第一个数b复制一份数据b。副本b与前一个数进行比较大小,如果b小于a,则a移入到b的位置,b插入到a的位置。
五、优化案例分析
待排序数据:8 6 2 3 1 5 7 4
第一轮排序:
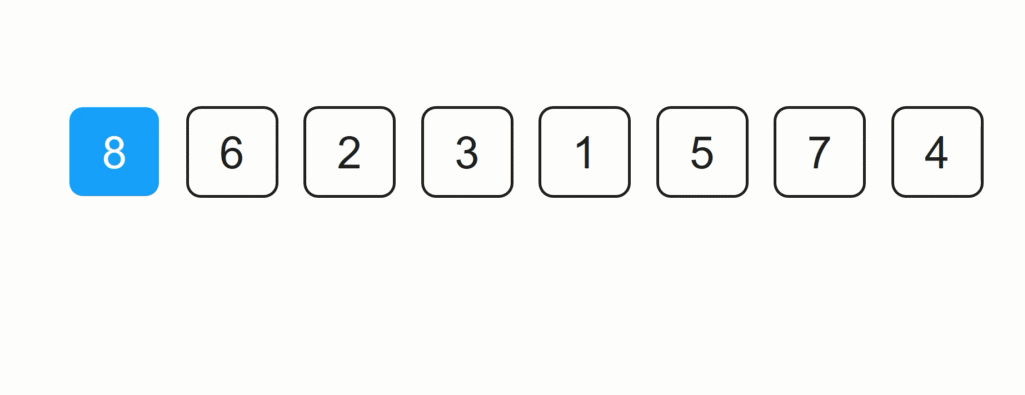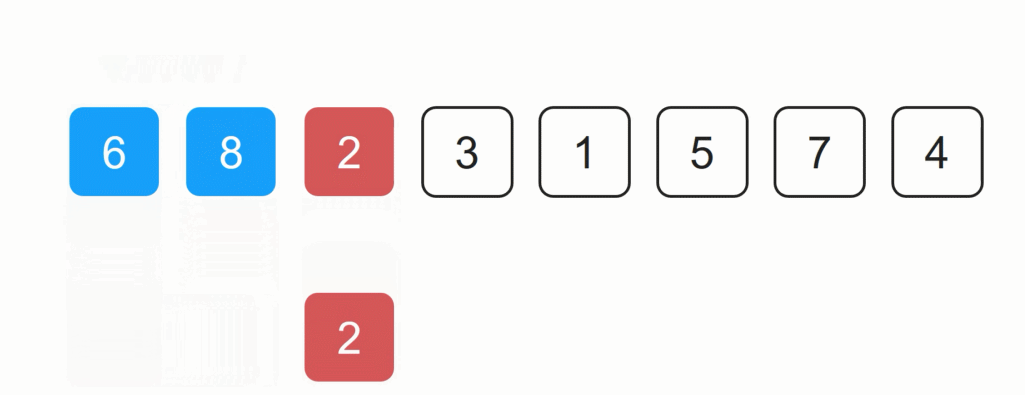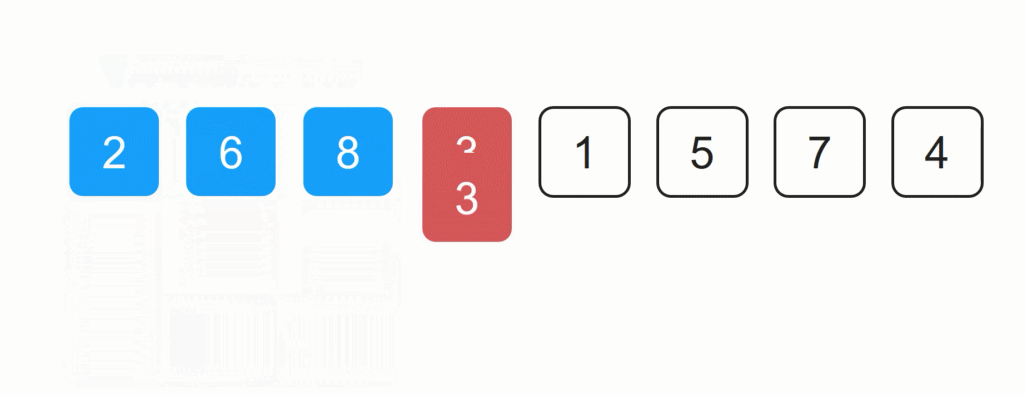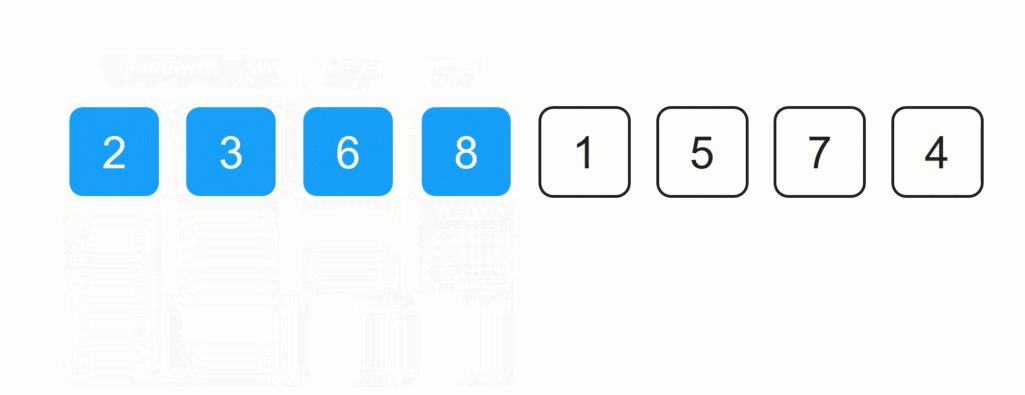
默认数字8已排序,剩余7个未排序集合中,数字6为未排序集合中的第一个数字,将其复制一份数据。6与8比较大小,6小于8,8移入到6的位置,6插入到8的位置。得到如下结果:
6 8 2 3 1 5 7 4
第二轮排序:
假设前2数字已排序,剩余6个未排序的集合中,数字2为未排序集合的第一个数字,将其复制一个数据。2与8比较大小,2小于8,8移入到2的位置,2再与6比较大小,2小于6,6移入到8之前的位置,2插入到6的位置。得到如下结果:
2 6 8 3 1 5 7 4
......
六、优化编码
public static void sortAdvance(int[] arr) {
int n = arr.length;
for (int i = 1; i < n; i++) {
// 拷贝数据
int e = arr[i];
// j保存元素e应该插入的位置
int j;
for (j = i; j > 0 && arr[j - 1] > e; j--) {
arr[j] = arr[j - 1];
}
arr[j] = e;
}
}

