比赛(补题)地址:http://222.22.65.164/problemset.php
题号为:4305 —— 4309
总述:这次新生赛难度偏于平和,但涵盖方面甚广,其中一道签到题是c语言题,并且有两道是hdu一百题的原题,一道简单的最小生成树,唯一“有些难度”的应该是一道数论题(毕竟本来自己就是搞数学的)。
A.沙漠骆驼
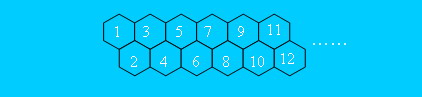
这是一道经典的递推问题,原型为HDU 2044的“一只小蜜蜂…”。思路很简单,以第5个沙丘为例,到达第五个沙丘的方式有两种:从第3个向 右走,或从第4个向右上走。设dp[ i ]为从第一个沙丘走到第i个的路径数,我们容易得到递推方程:
dp[5] = dp[4] + dp[3]
那么依此类推,得到一般的递推方程:
dp[ i ] = dp[ i-1 ] + dp[ i-2 ]
而从第a个到第b个,则可以简化为第1个到第b-a个。
1 ll f[100]; 2 3 void init() { 4 f[1] = f[2] = 1; 5 for (int i = 3; i < 100; i++) { 6 f[i] = f[i - 1] + f[i - 2]; 7 } 8 } 9 10 int main() { 11 init(); 12 13 int t; 14 scanf("%d", &t); 15 int a, b; 16 while (t--) { 17 scanf("%d%d", &a, &b); 18 printf("%lld ", f[b - a + 1]); 19 } 20 21 return 0; 22 }
B.炉石传说真好玩!
水题,原题是 HDU 2052 的 “Picture”,直接放代码:
1 int main() { 2 int n, m; 3 while (~scanf("%d%d", &n, &m)) { 4 putchar('+'); 5 for (int i = 0; i < n; i++) putchar('-'); 6 putchar('+'); 7 putchar(' '); 8 for (int i = 0; i < m; i++) { 9 putchar('|'); 10 for (int j = 0; j < n; j++) { 11 putchar(' '); 12 } 13 putchar('|'); 14 putchar(' '); 15 } 16 putchar('+'); 17 for (int i = 0; i < n; i++) putchar('-'); 18 putchar('+'); 19 putchar(' '); 20 putchar(' '); 21 } 22 23 return 0; 24 }
C.加油啊!奥托大人!
Emmm,这是一道裸的Kruskal,不理解的大家可以搜索一下,不想搜的也可以等数据结构老师讲,2333.
这道题的原题是 HDU 1863 的 “ 畅通工程”。
代码如下:
1 struct Edge { 2 int from, to, w; 3 4 Edge(int from = 0, int to = 0, int w = 0): 5 from(from), to(to), w(w) {} 6 7 bool operator < (const Edge &rhs) const { 8 return w < rhs.w; 9 } 10 } edge[MAXEDGE]; 11 12 int parents[MAXVERTEX]; 13 int vertices, edges; 14 15 void init() { 16 for (int i = 1; i < MAXVERTEX; i++) { 17 parents[i] = i; 18 } 19 } 20 21 int find(int x) { 22 if (parents[x] == x) { 23 return x; 24 } else { 25 return parents[x] = find(parents[x]); 26 } 27 } 28 29 bool unite(int x, int y) { 30 x = find(x); 31 y = find(y); 32 if (x == y) { 33 return true; 34 } else { 35 parents[y] = x; 36 } 37 return false; 38 } 39 40 int kruskal() { 41 init(); 42 sort(edge, edge + edges); 43 int ans = 0, counter = 1; 44 for (int i = 0; i < edges; i++) { 45 if (unite(edge[i].from, edge[i].to)) { 46 continue; 47 } else { 48 ans += edge[i].w; 49 counter++; 50 } 51 if (counter >= vertices) { 52 break; 53 } 54 } 55 if (counter >= vertices) { 56 return ans; 57 } else { 58 return -1; 59 } 60 } 61 62 int main() { 63 int u, v, w; 64 65 while (~scanf("%d%d", &edges, &vertices)) { 66 if (edges == 0) break; 67 for (int i = 0; i < edges; i++) { 68 scanf("%d%d%d", &u, &v, &w); 69 edge[i] = Edge(u, v, w); 70 } 71 72 int ans = kruskal(); 73 if (ans == -1) { 74 printf("? "); 75 } else { 76 printf("%d ", ans); 77 } 78 } 79 80 return 0; 81 }
D.大家快来%啊!
这。。。签到题就不用讲,也不用放代码了吧。
唯一需要注意的是纯c选手输出时需要将%转义。
E.R.I.P.
根据算数基本定理,任何一个自然数都可以唯一地分解为若干个素数的乘积,如果我们列出这个数所有的质因数,并写成幂的乘积的形式,则称其为标准素因数分解式:
比如:对于120,120 = 2*2*2*3*5,写成标准素因数分解式就是:
120 = 23 * 31 * 51
那么我们就可以轻易地得到 120 因子个数:所有幂次+1的乘积
也就是: ( 3 + 1 ) * ( 1 + 1 ) * ( 1 + 1 ) = 16
.....在此证明过程不再赘述
知道了这些,我们来考虑让一个数因子个数扩大到二倍(我们称其为一次“扩展”)的 “ 费用 ” :
我们可以将总的费用写为素因子幂的乘积的形式。
考虑这样实现:将总费用维护为一个堆(为什么要维护成堆?请认真思考),每个素因子的费用都保存在一个含有“ 底数,指数,值 ”的结构体中。
初始时堆中没有元素,通过不断进行“ 扩展 ”,逐渐向堆中增加元素,直到因子个数符合要求(500500)。
那么 最后每一个结构体中的值再除以底数(为什么要除以底数?请认真思考) 的乘积就是总的费用。
在考虑操作方法,不外乎有两种:
1、扩展一个新的(指数为0)的素因子(比如说取了 2),并标记为“新素数”(以待后用)。
同时对这个素因子的费用进行更新 2(0+1)->(1 + 1)
2、在堆中取扩展费用最小的素数,进行扩展(更新其指数),同时更新其费用。
如果这个素数是一个“新素数”,那么我们从打好的素数表中,取下一个素数(比如说取了2)进堆,将其指数初始化为0。
下边来看一下代码实现:
1 #include<bits/stdc++.h> 2 #define ll long long 3 using namespace std; 4 int MAXN=600000,curnum=0; 5 bool vis[10000000]; 6 vector<int> sushu; 7 int cursushu=0; 8 struct node{ 9 int dishu; 10 int zhishu; 11 ll zhi; 12 13 }; 14 bool operator<(node a,node b) 15 { 16 return a.zhi>b.zhi; 17 } 18 19 priority_queue<node> dui; 20 ll ans=1; 21 22 void dabiao(){ 23 for(ll i=2;;i++){ 24 if(!vis[i]){ 25 sushu.push_back(i); 26 } 27 if(sushu.size()>500500){ 28 break; 29 } 30 for(ll j=i*i;j<10000000;j+=i){ 31 vis[j]=true; 32 } 33 } 34 } 35 void addnew(int x){ 36 node p; 37 p.dishu=sushu[x]; 38 p.zhishu=1; 39 p.zhi=p.dishu; 40 dui.push(p); 41 } 42 43 44 void update_old_node(node tmp){ 45 node a; 46 a.dishu=tmp.dishu; 47 a.zhishu=tmp.zhishu*2; 48 a.zhi=1; 49 for(int i=0;i<a.zhishu;i++){ 50 a.zhi*=a.dishu; 51 } 52 dui.push(a); 53 } 54 55 void act(){ 56 node tmp=dui.top(); 57 dui.pop(); 58 if(tmp.dishu==sushu[cursushu-1]){ 59 addnew(cursushu++); 60 update_old_node(tmp); 61 } 62 else{ 63 update_old_node(tmp); 64 } 65 } 66 67 int main() 68 { 69 cout<<"Input N:"<<endl; 70 int n; 71 cin>>n; 72 dabiao(); 73 addnew(cursushu++); 74 for(int i=0;i<n;i++) 75 act(); 76 while(!dui.empty()){ 77 ans*=(dui.top().zhi/dui.top().dishu%500500507); 78 ans%=500500507; 79 dui.pop(); 80 } 81 cout<<ans; 82 }