注:下面的图G都为无向连通图
一、点支配
【支配】
对于图G中顶点集合V中的某一个点A与另一个点B有边链接,叫做点A支配B。
【点支配集】
对于图G中顶点集合V中的某个顶点子集V',可以支配V-V'中的其他点,这个点集V'就是点支配集。
【极小支配集】
对于支配集V,他的任何真子集都不是支配集,就称为V是极小支配集。
【最小支配集】
顶点数最小的支配集就是最小支配集。
注意:极小支配集和最小支配集不是一个含义。
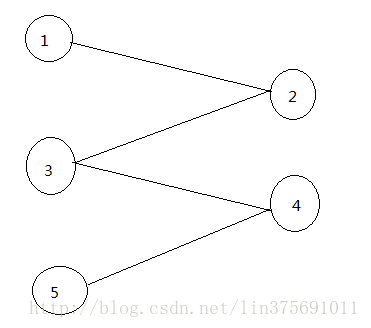
例如当前图中有一个极小支配集{1,3,5},因为他的任何真子集都不是支配集。但是最小支配集是{2,4}
【点支配数】
最小点支配集中点的个数被称为点支配数。
点支配集性质:当一个图没有孤立顶点时,如果V'是点支配集,那么V-V'也是点支配集。
二、点覆盖
【覆盖】
对于图G上的某一点A,已知有一边E与它链接,点A就覆盖了边E。(这里是点对于边的覆盖)
【点覆盖集】
对于图G,其顶点集合V的子集V'可以覆盖其边集合E中的所有边。那么V'就是点覆盖集。
【极小点覆盖集】
若点覆盖集V'的任何真子集都不是点覆盖集,则称V'是极小点覆盖集。
【最小点覆盖集】
顶点个数最少的点覆盖集称为最小点覆盖集。
注:极小点覆盖集和最小点覆盖集不是同一个概念,理由同极小点支配集和最小点支配集。
【点覆盖数】
最小点覆盖集中的顶点数称为点覆盖数。
三、点独立
【独立】
在图G中,如果点A与点B没有边直接相连,两点间不相邻。就称这两点间独立。(这里是关于点的独立)
【点独立集】
在图G中,顶点集合V的子集V'中的任何两点间均独立,则称V'为点独立集。
【极大点独立集】
若向顶点子集V'中再加入任何其他顶点时V'都不将是点独立集,就称V'是极大点独立集。
【最大点独立集】
顶点数最多的点独立集就是最大点独立集。
【点独立数】
最大点独立集中顶点的个数称为点独立数。
四、边覆盖
【覆盖】
在图G中,对于某一条边E与他的两端点A、B,我们称E覆盖了点A、B。(这里是关于边的覆盖)
【边覆盖集】
在图G中,对于边的集合E的子集E'其中的所有边可以把图G中的顶点集合V中的所有点覆盖,则称E'为边覆盖集。
【极小边覆盖集】
若边覆盖集E'的任何真子集都不是边覆盖集,则称E'为极小边覆盖集。
【最小边覆盖集】
边数最少的边覆盖集称为最小边覆盖集。
【边覆盖数】
最小边覆盖集中的边的数量称为边覆盖数。
五、边独立(匹配)
【独立】
在图G中,若边A与边B没有公共顶点,则称这两条边相互独立。(这里是边独立)
【边独立集(匹配)】
在图G中,对于边的集合E的子集E',其中的任何两条边均独立,集合E'就称为边独立集。也称为E'为图G的匹配
【极大匹配(极大边独立集)】
在图G中,对于边的集合E的子集E',如果E'为边独立集且再加入任何一条边都不再是边独立集,则E'被称为极大匹配(极大边独立集)。
【最大匹配(最大边独立集)】
边数最多的匹配称为最大匹配(最大边独立集)。
【边独立数】
最大匹配中边的数量叫做边独立数
【盖点与未盖点】
对图G(U,V)给定的匹配M来说:
1、如果顶点集合V中某点v是M中某个边的端点,则称v是M的盖点。
2、如果顶点集合V中某点v不是M中任何边的端点,则称v是M的未盖点。