
论文题目:Forward and Backward Information Retention for Accurate Binary Neural Networks
文献地址:https://arxiv.org/abs/1909.10788
源码地址: https://github.com/htqin/IR-Net
IR-Net应用中的效果
作者使用了两个基准数据集:CIFAR-10和ImageNet(ILSVRC12)进行了实验。在两个数据集上的实验结果表明,IR-Net比现有的最先进方法更具竞争力。
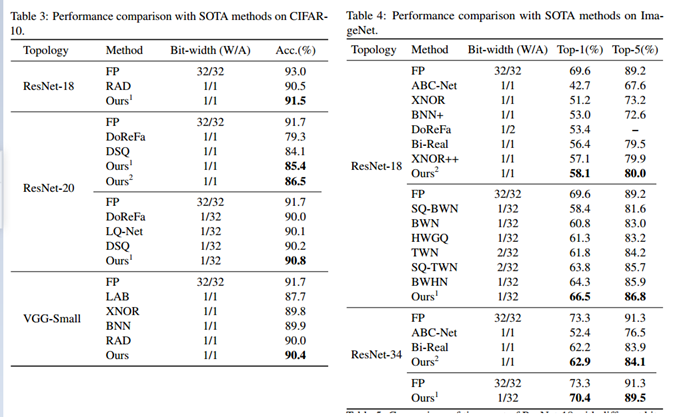
为了进一步验证IR-Net在实际移动设备中的部署效率,作者在1.2GHz 64位四核ARM Cortex-A53的Raspberry Pi 3B上进一步实现了IR-Net,并在实际应用中测试了其真实速度。
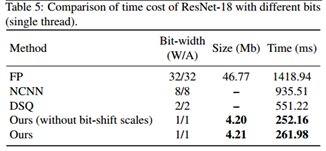
从上表可以看出,IR-Net的推理速度要快得多,模型尺寸也大大减小,而且IR-Net中的位移操作几乎不会带来额外的推理时间和存储消耗。
二值化网络的现状与动机
权值和激活二值化是一种有效的深度神经网络压缩方法,可以利用位操作加速推理。并且,在实际使用中,二进制神经网络以其微小的存储空间和高效的推理能力受到了社会的广泛关注。虽然许多二值化方法通过最小化前向传播的量化误差来提高模型的精度,但二值化模型与全精度模型之间仍存在明显的性能差距。
二进制神经网络的性能退化主要原因是由于其表示能力有限和二值化的离散性,导致其在前向和反向传播中都存在严重的信息丢失。在前向传播中,当激活量和权值限制为两个值时,模型的多样性急剧下降,而多样性被证明是神经网络[54]的高精度的关键。
多样性意味着在前向传播的过程中会有携带足够信息的能力,同时,在反向传播的过程中,精准的梯度会给优化提供正确的信息。然而,二值化网络在训练过程中,离散的二值往往带来不准确的梯度和错误的优化方向。所以,作者认为二值化网络中的量化损失是信息在前向传播和反向传播两个方面丢失造成的。
因此,提出了信息保持网络IR-Net(Information Retention Network):
- 在前向传播中引入了一种称为Libra参数二值化(Libra-PB)的平衡标准化量化方法,通过量化参数的信息熵最大和量化误差最小,使正向传播中的信息损失最小;
- 在反向传播中采用误差衰减估计器(EDE)来计算梯度,通过更好地逼近 sign 函数来最小化信息损失,保证训练开始时的充分更新和训练结束时的精确梯度。
如下图所示,第一幅中描绘了Libra-PB在前向过程中改变权重分布的示意图;第二幅图中描绘了Libra-PB和EDE在真个训练过程中的使用情况;第三幅图中描绘了EDE通过逼近sign函数来最小化信息损失的过程。
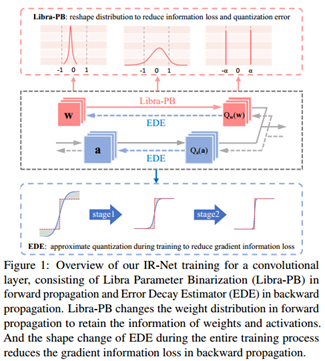
IR-Net
Preliminaries
a. 常规运算
在深度神经网络中,主要的运算可以表达为:
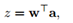
其中,w表示权重向量;a表示输入的激活向量。
b. 二值化的过程
需要对权重w和输入a进行二值化,下述Qx(x)是分别进行权重w和输入a二值化的过程,即要么是Qw(w),要么是Qa(a)。α为各自的标量系数。
网络二值化的目标是用1-bit表示浮点权值和各层经过激活函数后的输出。一般来说,量化可以表述为:

其中,x为浮点参数,包括浮点权值w和激活输出a,Bx∈{-1, +1}表示二值,包括二值权重Bw和激活输出Ba。α表示为二值标量,包括权重标量αw和输出激活叫来那个αa。通常使用sign函数获取Bx:
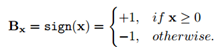
c. 二值化网络的运算
当获得二值化后的权重Qw(w)和二值化后的输入Qa(a)后,便可以沿用常规运算的形式计算二值化网络的运算,如下所示:
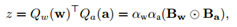
其中,包含的操作为XNOR运算。
采用符号函数进行量化,在反向传播过程中就会存在一个问题:符号函数的导数几乎处处为0,这和反向传播不相符。因为在离散化(预激活或权值)之前原始值的精确梯度将为零。因此,通常使用"直通估计器(STE)[5]"来训练二元模型,模型通过恒等或Hardtanh函数来传播梯度。
前向传播中的Libra-PB (Libra Parameter Binarization)
传统最小化量化误差的目标函数
在前向传播过程中,量化操作会带来信息损失。在许多卷积神经网络二值化的量化中,都将最小化量化误差的方式作为优化的目标函数:

其中,x表示全精度参数;Qx(x)表示量化参数;J(Qx(x))表示量化损失。
对于二值模型,其参数的表示能力被限制为两个值,使得神经元携带的信息容易丢失。二值神经网络的解空间与全精度神经网络的解空间也有很大的不同。因此,如果不通过网络保持信息,仅通过最小化量化误差来保证良好的二值化网络是不够的,也是困难的。
因此,作者结合量化损失和信息损失,在前向计算过程中,提出Libra-PB保持信息的同时最小化信息损失。
Libra-PB目标函数
对于随机数b∈{-1, +1},服从伯努利分布,此处的b实际上就是量化后的Qw(w)和Qa(a)。其概率分布可以表示为如下形式:
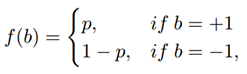
参数二值化的过程本质上是权重的初始化和输入的二值化。作者希望二值化得到的权重能够分布均衡,也就是说,让Qx(x)的信息熵越大越好,越大则越混乱,分布也就越均衡。
对于二值化结果Qx(x)进行信息熵的求取,实际上也就是Bx的信息熵的求取(由网络二值化过程的公式可得)。因此,可以表达为如下形式:
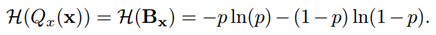
并且,当p=0.5时,信息熵最大。也就意味着量化后的值均匀分布。
Libra-PB的目标函数定义为:
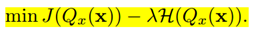
此外,为了使训练更加稳定,避免因权值和梯度而产生的负面影响,进一步对平衡权值进行了归一化处理。
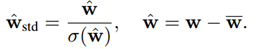
其中,σ( · )为标准差。
权重w^具有两个特点:
(1) 零均值,使获得的二值化权重信息熵最大。
(2) 单位范数,这使得二值化所涉及的全精度权重更加分散。
从下图中可以看出,权重是从全精度权重变换到二值权重,Libra-PB二值化后的权重相较于传统的二值化具有更高的信息熵,分布更加均衡。
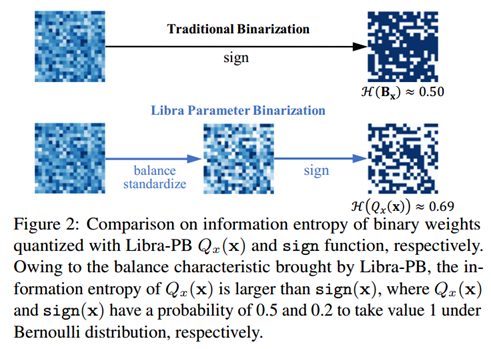
因此最终,针对正向传播的Libra参数二值化可以表示如下:
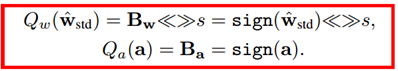
R-Net的主要运算操作可以表示为:

其中,<<>>表示左移右移操作。s可由下述表达式计算得到:
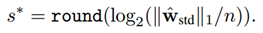
反向传播中的EDE(Error Decay Estimator)
由于二值化的不连续性,梯度的近似是后向传播不可避免的。因此,量化的影响无法用近似准确地建模,造成了巨大的信息损失。近似可以表示为:
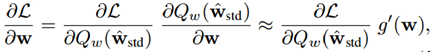
其中,L(w)表示损失函数,g(w)表示sign 函数的近似表达式。对于g(w)通常有两种近似方法:
- Identity:y = x
Identity 函数直接将输出值的梯度信息传递给输入值,完全忽略了二值化的影响。如图 3(a) 的阴影区域所示,梯度误差很大,并且会在反向传播过程中累积。利用随机梯度下降算法,要求保留正确的梯度信息,避免训练不稳定,而不是忽略由 Identity 函数引起的噪声。
- Clip: y=Hardtanh(x)
Clip 函数考虑了二值化的截断属性,减少了梯度误差。但它只能在截断间隔内传递梯度信息。从图 3(b) 中可以看出,对于 [-1,+1] 之外的参数,梯度被限制为 0。这意味着一旦该值跳出截断间隔,就无法再对其进行更新。这一特性极大地限制了反向传播的更新能力,证明了 ReLU 是一个比 Tanh 更好的激活函数。因此,在实际应用中,Clip 近似增加了优化的难度,降低了精度。确保足够的更新可能性至关重要,特别是在训练过程开始时。
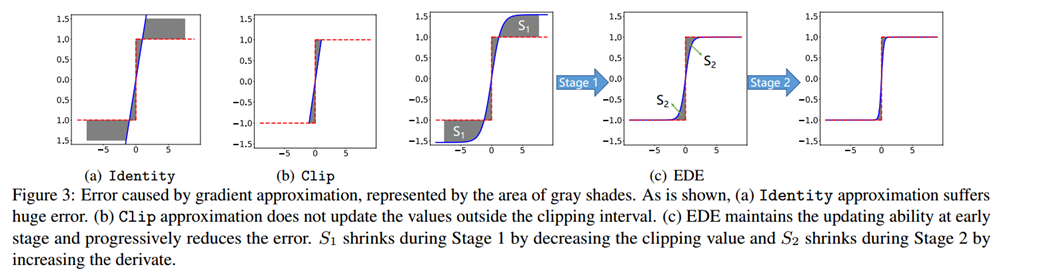
Identity 函数丢失了量化的梯度信息,而 Clip 函数则丢失了截断间隔之外的梯度信息。这两种梯度信息损失之间存在矛盾。
为了保留反向传播中由损失函数导出的信息,EDE 引入了一种渐进的两阶段近似梯度方法。
第一阶段:保留反向传播算法的更新能力。我们将梯度估计函数的导数值保持在接近 1 的水平,然后逐步将截断值从一个大的数字降到 1。利用这一规则,我们的近似函数从 Identity 函数演化到 Clip 函数,从而保证了训练早期的更新能力。
第二阶段:保持参数的精确梯度在 0 左右。我们将截断值保持为 1,并逐渐将导数曲线演变到阶梯函数的形状。利用这一规则,我们的近似函数从 Clip 函数演变到 sign 函数,从而保证了前向和反向传播的一致性。
各阶段EDE的形状变化如图3(c)所示。通过该设计,EDE减小了前向二值化函数和后向近似函数之间的差异,同时所有参数都能得到合理的更新。