• leetcode常规算法题复盘（第六期）——最小体力消耗路径

    题目原文

    1631. 最小体力消耗路径

    你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。

    一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

    请你返回从左上角走到右下角的最小体力消耗值 。

    示例 1：

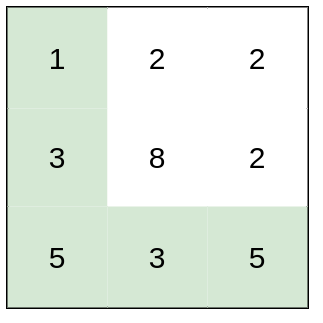
    输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路劲差值最大值为 3 。

    示例 2：

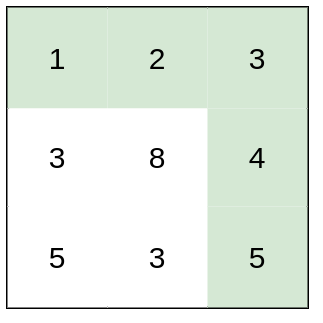
    输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

    示例 3：

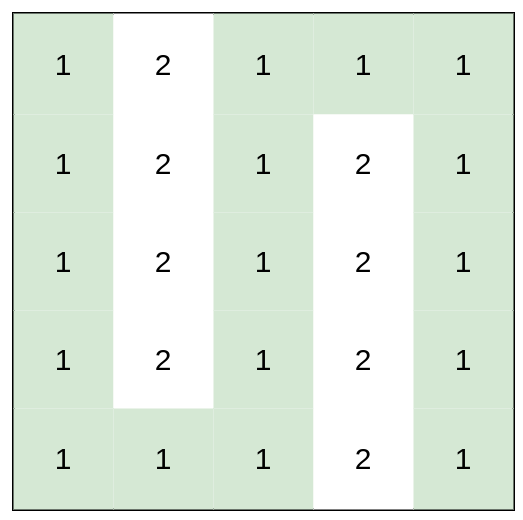
    输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

    提示：

    • rows == heights.length
    • columns == heights[i].length
    • 1 <= rows, columns <= 100
    • 1 <= heights[i][j] <= 106

    尝试解答

     这道题虽然是被评为中等难度，知识丰富度绝不在某些困难题之下，奈何楼主只是积累得实在太少，这道题死活都写不过，于是楼主决定认真学习一下大佬们解决这道题的思路。

    标准题解

     思路一：二分思路+BFS算法（广度优先搜索）

    我最初的思路更接近于BFS跟DFS，DFS似乎会有很多判定条件，规律难找得要命，之后我有有了一个BFS的思路，就是将差值从0往上涨，直到能走通到终点为止，然而没写出来，原因应该是对BFS不够了解（哭）。

    先上代码：

     1      public int minimumEffortPath(int[][] heights) {
 2             int L = 0, R = 1_000_000; //
 3             while (L <= R) {
 4                 int M = (L + R) >> 1; // 取mid
 5                 if (bfs(M, heights)) {
 6                     R = M - 1;
 7                 } else {
 8                     L = M + 1;
 9                 }
10             }
11             return L;
12         }
13 
14 
15         /**
16          * 能否小于max的情况下找到一条从起点到终点的路径
17          *
18          * @param max
19          * @param heights
20          * @return
21          */
22         int[][] directions = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
23         int m, n;
24 
25         private boolean bfs(int max, int[][] heights) {
26             m = heights.length;
27             n = heights[0].length;
28             Queue<int[]> queue = new LinkedList<>();
29             queue.add(new int[]{0, 0});
30             boolean[][] vis = new boolean[m][n];
31             vis[0][0] = true;
32             while (!queue.isEmpty()) {
33                 int[] curr = queue.poll();
34                 int i = curr[0], j = curr[1];
35                 if (i == m - 1 && j == n - 1) return true;
36                 for (int[] d : directions) {
37                     int ni = i + d[0], nj = j + d[1];
38                     //判断(i,j) --> (ni,nj)的距离是否比当前的小距离小，如果是这点是有效的
39                     if (inArea(ni, nj) && !vis[ni][nj] && Math.abs(heights[i][j] - heights[ni][nj]) <= max) {
40                         vis[ni][nj] = true;
41                         queue.add(new int[]{ni, nj});
42                     }
43                 }
44             }
45             return false;
46         }
47 
48         private boolean inArea(int i, int j) {
49             return i >= 0 && i < m && j >= 0 && j < n;
50         }
51 
52 
53 
54 //作者：a-fei-8
55 //链接：https://leetcode-cn.com/problems/path-with-minimum-effort/solution/zui-xiao-ti-li-xiao-hao-lu-jing-by-a-fei-8/
56 //来源：力扣（LeetCode）
57 //著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

    题目要求的是找到一条路径，在这个路径上，消耗的体力值最小， 可以转化成，给定一个固定的体力值，是否能达到这找到一条路径到达终点

    根据题意给出的1-1000000的范围，max值至多为这个区间，不断缩小这个区间的范围，bfs函数来判断是否能有这样一条路径

    作者：a-fei-8
    链接：https://leetcode-cn.com/problems/path-with-minimum-effort/solution/zui-xiao-ti-li-xiao-hao-lu-jing-by-a-fei-8/
    来源：力扣（LeetCode）
    著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

    我觉得应该在这里补一下BFS与DFS的知识，如下所示：

    BFS：广度优先搜索

    DFS：深度优先搜索

    树的遍历

    BFS：A   B C D  E F  G  H I

    DFS:  A B  C E  F  D G H  I

    图的遍历

    从A出发

    BFS：A  B  C  D  E  F （其中一种）

    DFS：A  B  D  F  E  C （其中一种）

    数据结构

    BFS： 队列（先进先出）

    步骤：1、首先A入队列，

                2、A出队列时，A的邻接结点B，C相应进入队列 

                3、B出队列时，B的邻接结点A，C，D中未进过队列的D进入队列

                4、C出队列时，C的邻接结点A，B，D，E中未进过队列的E进入队列

                5、D出队列时，D的邻接结点B，C，E，F中未进过队列的F进入队列

                6、E出队列，没有结点可再进队列

                7、F出队列

    DFS：栈（先进后出）

    步骤：1、首先A入栈，

                2、A出栈时，A的邻接结点B，C相应入栈  （这里假设C在下，B在上）

                3、B出栈时，B的邻接结点A，C，D中未进过栈的D入栈

                4、D出栈时，D的邻接结点B，C，E，F中未进过栈的E、F入栈（假设E在下，F在上）

                5、F出栈时，F没有邻接结点可入栈

                6、E出栈，E的邻接结点C，D已入过栈

                7、C出栈

    代码（Python）

    1、图有两种表示方式，邻接矩阵和邻接表

          这里用python字典结构表示:

    BFS

    DFS

    非递归

    能用栈的地方都能用递归

    递归

    DFS递归和非递归的结果不同，非递归：A C E D F B    递归：A B C D E F

    此外，深度优先搜索和广度优先搜索的结果都不唯一。


    作者：Joe_Chestnut
    链接：https://www.jianshu.com/p/0a597adfc1e8
    来源：简书
    著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
    了解了BFS与DFS后，对大佬的代码瞬间就看懂了！（今天又进步了一点～真开心[x]）
    思路二：DFS算法（深度优先搜索）（超时）
    先上代码：
     1         int INF = Integer.MAX_VALUE >> 1;
 2         int ans = INF;
 3         int[][] directions = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
 4         int m, n;
 5         boolean[][] vis;
 6 
 7         Map<Integer, Integer> memo = new HashMap<>();
 8 
 9 
10         public int minimumEffortPath(int[][] heights) {
11             m = heights.length;
12             n = heights[0].length;
13             vis = new boolean[m][n];
14             vis[0][0] = true;
15             dfs(heights, 0, 0, 0);
16             return ans;
17         }
18 
19 
20         private void dfs(int[][] heights, int i, int j, int val) {
21             if (i == m - 1 && j == n - 1) {
22                 if (ans >= val) ans = val;
23                 return;
24             }
25             for (int[] d : directions) {
26                 int ni = i + d[0], nj = j + d[1];
27                 if (inArea(ni, nj) && !vis[ni][nj]) {
28                     vis[ni][nj] = true;
29                     dfs(heights, ni, nj, Math.max(Math.abs(heights[ni][nj] - heights[i][j]), val));
30                     vis[ni][nj] = false;
31                 }
32             }
33         }
34 
35 
36         private boolean inArea(int i, int j) {
37             return i >= 0 && i < m && j >= 0 && j < n;
38         }
39 
40 
41 //作者：a-fei-8
42 //链接：https://leetcode-cn.com/problems/path-with-minimum-effort/solution/zui-xiao-ti-li-xiao-hao-lu-jing-by-a-fei-8/
43 //来源：力扣（LeetCode）
44 //著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

     在这里可否看出来回溯算法一般是与深度优先算法同时出现的？

    思路三：Dijkstra法（迪杰斯特拉方法）

    先上代码，dist[i][j]表示起点(0,0)到(i,j)的某条路径上的相邻点的差值的最大值（即一条路径上的最小消耗值）

     1         int[][] directions = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
 2         int m, n;
 3         int[][] dist; //距离
 4         boolean[][] vis; //访问数组
 5         int INF = Integer.MAX_VALUE; //INF
 6 
 7 
 8         class Node {
 9             int i;
10             int j;
11             int val;
12 
13             public Node(int i, int j, int val) {
14                 this.i = i;
15                 this.j = j;
16                 this.val = val; //距离
17             }
18         }
19 
20 
21         public int minimumEffortPath(int[][] heights) {
22             m = heights.length;
23             n = heights[0].length;
24             dist = new int[m][n];
25             vis = new boolean[m][n];
26             for (int i = 0; i < m; i++) Arrays.fill(dist[i], INF);
27             PriorityQueue<Node> pq = new PriorityQueue<>((o1, o2) -> o1.val - o2.val);
28             pq.offer(new Node(0, 0, 0));
29             dist[0][0] = 0;
30             while (!pq.isEmpty()) {
31                 Node curr = pq.poll();
32                 int i = curr.i, j = curr.j, val = curr.val;
33                 if (vis[i][j]) continue;
34                 vis[i][j] = true;
35                 for (int[] d : directions) {
36                     int ni = i + d[0], nj = j + d[1];
37                     if (!inArea(ni, nj)) continue;
38                     int nval = Math.max(val, Math.abs(heights[i][j] - heights[ni][nj]));
39                     //松弛
40                     if (!vis[ni][nj] && dist[ni][nj] > nval) {
41                         dist[ni][nj] = nval;
42                         pq.offer(new Node(ni, nj, nval));
43                     }
44                 }
45             }
46             return dist[m - 1][n - 1];
47         }
48 
49 
50         private boolean inArea(int i, int j) {
51             return i >= 0 && i < m && j >= 0 && j < n;
52         }
53 
54 //作者：a-fei-8
55 //链接：https://leetcode-cn.com/problems/path-with-minimum-effort/solution/zui-xiao-ti-li-xiao-hao-lu-jing-by-a-fei-8/
56 //来源：力扣（LeetCode）
57 //著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

    我们先学习一下迪杰斯特拉法的原理：

    迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。 它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。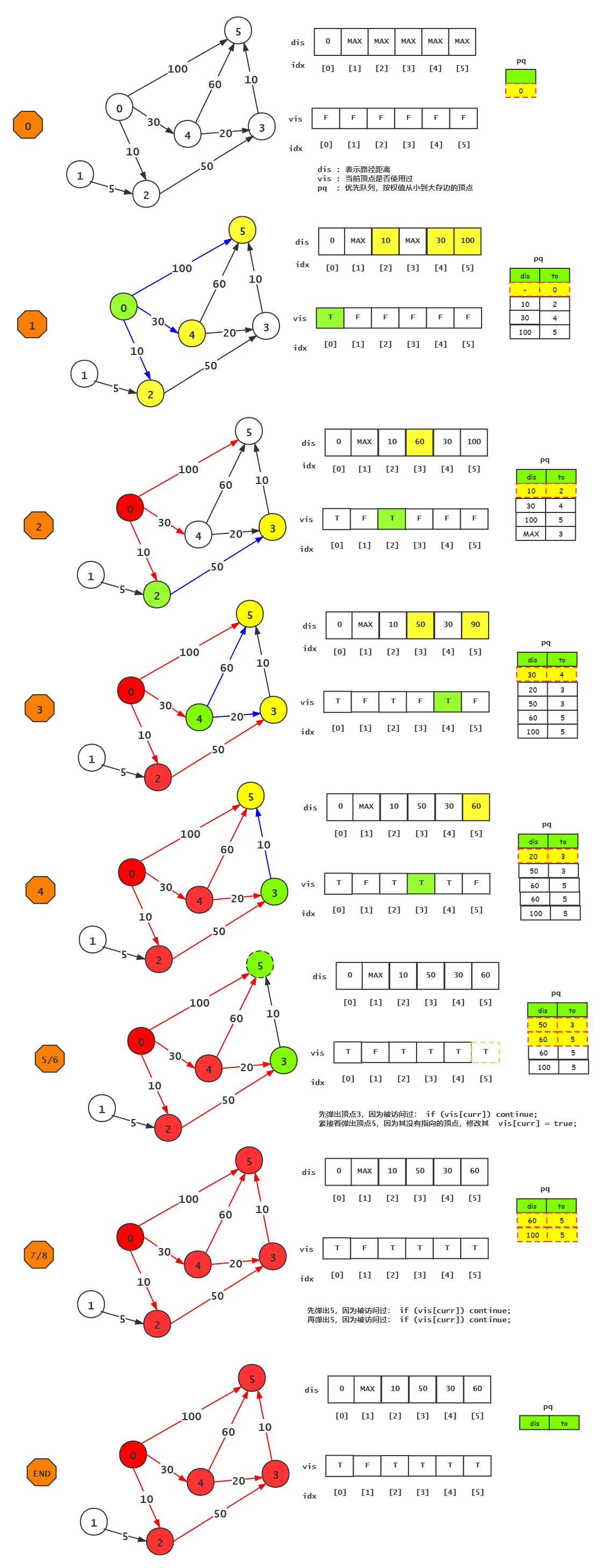

     上面这个图pq队列理解起来有些困难，需要记住它的本质是BFS，但又跟原生的BFS搜索顺序有些许不同，原生BFS搜索顺序往往是从左到右或从右到左，而且为了保证不再重复搜索节点，会设置一个容器来“记住”已经搜索过的节点，而在这里不一样，同一个节点我们可能需要多次搜索到才能确定它的最小路径，因此把容器去掉了，搜索顺序根据当前节点到下一点的距离值从小到大排序（实例中的java代码并没有体现这一点）

    基本思想

    1. 通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。
    2. 此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。
    3. 初始时，S中只有起点s；U中是除s之外的顶点，并且U中顶点的路径是”起点s到该顶点的路径”。然后，从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 然后，再从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 … 重复该操作，直到遍历完所有顶点。

    操作步骤

    1. 初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为”起点s到该顶点的距离”[例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为∞]。
    2. 从U中选出”距离最短的顶点k”，并将顶点k加入到S中；同时，从U中移除顶点k。
    3. 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。
    4. 重复步骤(2)和(3)，直到遍历完所有顶点。

     

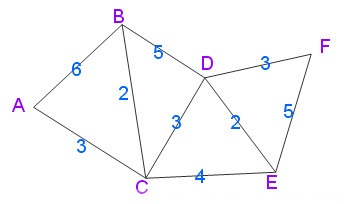
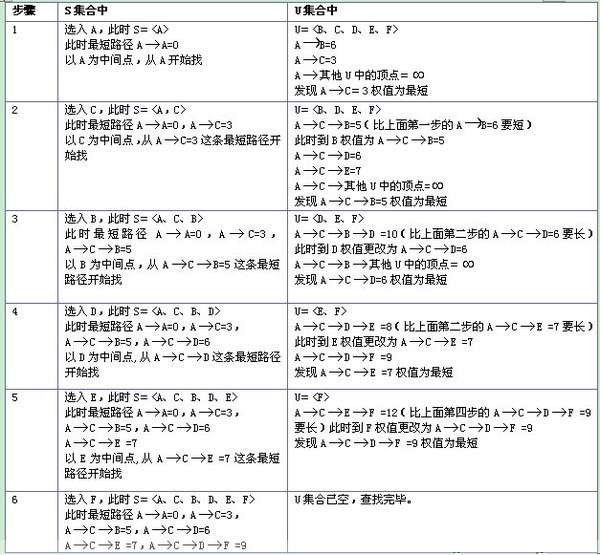
    单纯的看上面的理论可能比较难以理解，下面通过实例来对该算法进行说明。

     1   /**
 2      * @param edges 传入的边
 3      * @param s     起始顶点
 4      * @param n
 5      * @return
 6      */
 7     public int[] dijkstra(int[][] edges, int s, int n) {
 8         Map<Integer, List<int[]>> graph = new HashMap<>();
 9         for (int[] edge : edges)
10             graph.computeIfAbsent(edge[0], e -> new ArrayList<>()).add(new int[]{edge[1], edge[2]});
11         int[] dis = new int[n];
12         Arrays.fill(dis, Integer.MAX_VALUE);
13         boolean[] vis = new boolean[n];
14         dis[s] = 0;
15         PriorityQueue<Integer> pq = new PriorityQueue<>(((o1, o2) -> dis[o1] - dis[o2]));
16         pq.offer(s);
17         while (!pq.isEmpty()) {
18             int curr = pq.poll();
19             if (vis[curr]) continue;
20             vis[curr] = true;
21             List<int[]> nexts = graph.getOrDefault(curr, new ArrayList<>());
22             for (int[] next : nexts) {
23                 int to = next[0];
24                 int weigh = next[1];
25                 if (vis[to]) continue;
26                 if (dis[to] > dis[curr] + weigh) {
27                     dis[to] = dis[curr] + weigh;
28                 }
29                 pq.offer(to);
30             }
31         }
32         return dis;
33     }

    测试

     1  private void testOne() {
 2         int n = 6;//顶点数量
 3         int s = 0;//起点的下标索引
 4         int e = 8;//边的数量
 5         int[][] edges = new int[e][3];
 6         edges[0] = new int[]{0, 2, 10};
 7         edges[1] = new int[]{0, 4, 30};
 8         edges[2] = new int[]{0, 5, 100};
 9         edges[3] = new int[]{1, 2, 5};
10         edges[4] = new int[]{2, 3, 50};
11         edges[5] = new int[]{3, 5, 10};
12         edges[6] = new int[]{4, 3, 20};
13         edges[7] = new int[]{4, 5, 60};
14 //        System.out.println(JSON.toJSONString(edges));
15         dijkstra(edges, s, n);
16     }

     

     

     

     思路四：并查集

    这里先放几个小技巧：

    技巧1：二维矩阵按索引拍平到一维数组

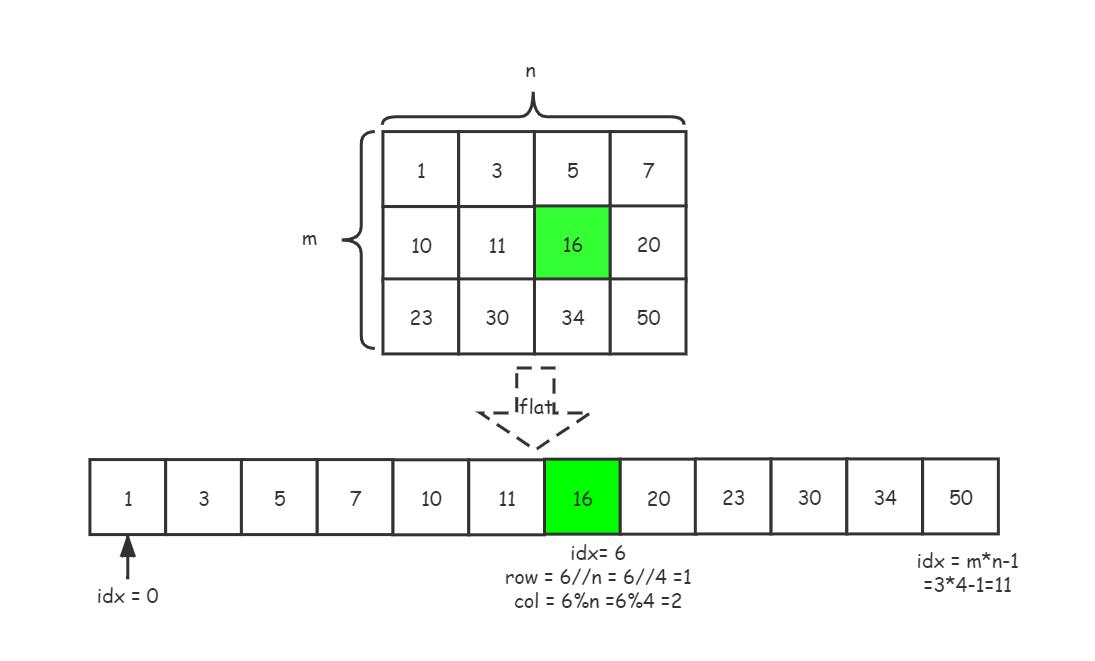
    • 如下图所示，每一个二维矩阵对应的，按第1行到第m行依次排列所得到的一维数组的坐标，可以互相转换
    如第2行第3列的16这个数，其矩阵的坐标是(1,2),而映射到一维数组的时候，其对应的下标索引idx=6
idx=6=i*n+j=1*4+2=6
而如何通过idx=6反向得到矩阵的坐标呢？
i=idx/n=6/4 =1
j=idx%n=6%4 =2
得到矩阵的坐标为(i,j) ==>(1,2)

    74_1

    技巧2：将矩阵当成二进制转化成十进制

    背景知识

    • 对于十进制整数 x，我们可以用 x & 1 得到 x 的二进制表示的最低位，它等价于 x % 2 ：

      • 例如当 x = 3 时，x 的二进制表示为 11，x & 1 的值为 1；

      • 例如当 x = 6 时，x 的二进制表示为 110，x & 1 的值为0。

    • 对于十进制整数 x，我们可以用 x & (1 << k) 来判断 x 二进制表示的第 k 位（最低位为第 0 位）是否为 1。如果该表达式的值大于零，那么第 k 位为 1：

      • 例如当 x = 3 时，x 的二进制表示为 11，x & (1 << 1) = 11 & 10 =10 >0，说明第 1 位为 1；
      • 例如当 x = 5 时，x 的二进制表示为 101，x & (1 << 1)= 101 & 10 = 0，说明第 1 位不为 1。

    举例

    给定一个矩阵：

    [[0, 0, 1],
[1, 0, 0],
[0, 1, 1]]

    该矩阵如果按每行依次排开的话，可以转换成一维矩阵

    [0, 0, 1, 1, 0, 0, 0, 1, 1]

    将上述的一维矩阵看成一个二进制的数是：

    001100011

    对应的十进制是99

    怎么转化

    • 一个矩阵转化成二进制数再转化成十进制数：
     1   /**
 2          * 
 3          * @param matrix 二维矩阵
 4          * @param R 矩阵的行数
 5          * @param C 矩阵的列数
 6          * @return
 7          */
 8         private int encode(int[][] matrix, int R, int C) {
 9             int x = 0;
10             for (int r = 0; r < R; r++) {
11                 for (int c = 0; c < C; c++) {
12                     x = x * 2 + matrix[r][c];
13                 }
14             }
15             return x;
16         }
    • 一个十进制的数如何转化为二进制的矩阵：
     1   /**
 2          * @param x 源数
 3          * @param R 矩阵的行数
 4          * @param C 矩阵的列数
 5          * @return
 6          */
 7         private int[][] decode(int x, int R, int C) {
 8             int[][] matrix = new int[R][C];
 9             for (int r = R - 1; r >= 0; r--) {
10                 for (int c = C - 1; c >= 0; c--) {
11                     matrix[r][c] = x & 1;
12                     x >>= 1;
13                 }
14             }
15             return matrix;
16         }

    之后就是并查集关于并查集的内容：

     

     1 class UnionFindSet:
 2     def UnionFindSet(n):
 3         parents = [0,1...n] # 记录每个元素的parent即根节点 先将它们的父节点设为自己
 4         ranks =[0,0...0]    # 记录节点的rank值
 5     
 6     # 如下图 递归版本 路径压缩(Path Compression)
 7     # 如果当前的x不是其父节点，就找到当前x的父节点的根节点(find(parents[x])) 并将这个值赋值给x的父节点
 8     def find(x):
 9         if ( x !=parents[x]): # 注意这里的if
10             parents[x] = find(parents[x])
11         return parents[x]
12 
13     # 如下图 根据Rank来合并(Union by Rank)
14     def union(x,y):
15         rootX = find(x) # 找到x的根节点rootX
16         rootY = find(y) # 找到y的根节点rootY
17         #取rank值小的那个挂到大的那个节点下面，此时两个根节点的rank值并没有发生变化，还是原来的值
18         if(ranks[rootX]>ranks[rootY]): parents[rootY] = rootX 
19         if(ranks[rootX]<ranks[rootY]): parents[rootX] = rootY
20         # 当两个rank值相等时，随便选择一个根节点挂到另外一个跟节点上，但是被挂的那个根节点的rank值需要+1    
21         if(ranks[rootX] == ranks[rootY] ):
22             parents[rootY] = rootX
23             ranks[rootY]++
24 
25 #作者：a-fei-8
26 #链接：https://leetcode-cn.com/problems/redundant-connection/solution/yi-wen-zhang-wo-bing-cha-ji-suan-fa-by-a-fei-8/
27 #来源：力扣（LeetCode）
28 #著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

     

     1     def find(x):
 2         rootX = x # 找到x的根节点
 3         while (rootX!=parents[rootX]):
 4             rootX = parents[rootX]
 5         curr = x # 准备一个curr变量
 6         while (curr!=rootX):
 7             next = parents[curr] # 暂存curr的父节点
 8             parents[curr] = rootX # 将curr节点的父节点设置为rootX
 9             curr = next # curr节点调到下个节点
10         return rootX

     

     

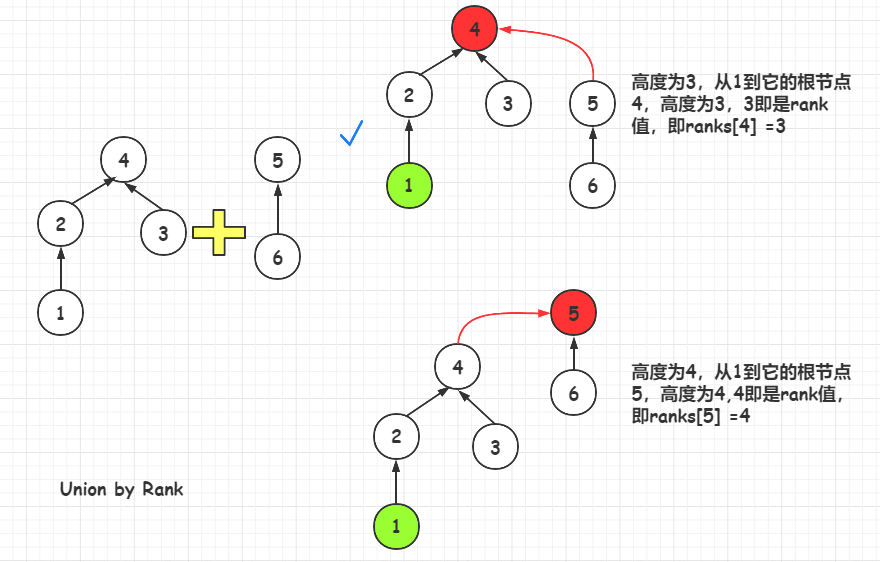
    根据Rank来合并(UnionUnion byby RankRank)

     

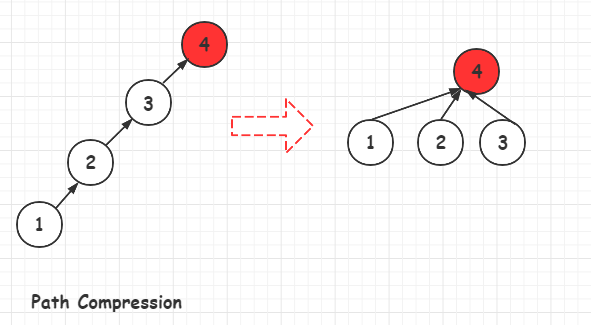
    路径压缩(PathPath CompressionCompression)

     

    应用

    1.被围绕的区域

     

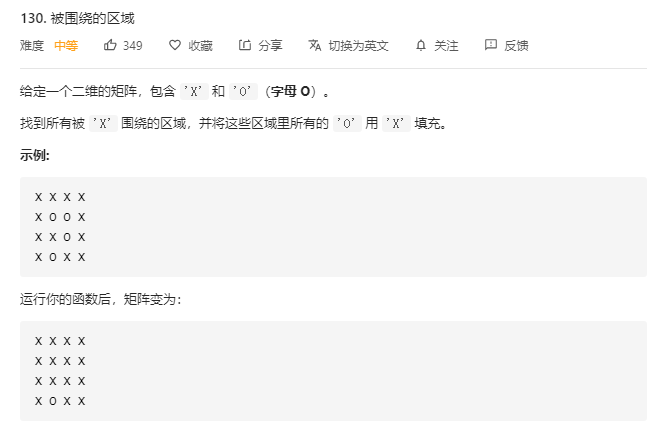
    思路

    • 准备一个并查集UnionFindSetUnionFindSet,初始化时，多一个节点设置为哑结点dummydummy
    • 因为是二维矩阵的缘故，可以将其坐标转化为一维矩阵，i * 列数 + ji∗列数+j
    • 边缘处的OO直接与dummydummy 进行合并
    • 非边缘的OO则需要上下左右四个方向探测，进行合并
    • 遍历，当发现当前节点与dummydummy节点的根节点相同，即联通的话，这个点维持不变

    并查集

     1         static class UnionFindSet {
 2             int[] parents;
 3             int[] ranks;
 4 
 5             public UnionFindSet(int n) {
 6                 parents = new int[n];
 7                 ranks = new int[n];
 8                 for (int i = 0; i < n; i++) {
 9                     parents[i] = i;
10                 }
11             }
12 
13 
14             public int find(int x) {
15                 if (x != parents[x]) {
16                     parents[x] = find(parents[x]);
17                 }
18                 System.out.println(x + ":" + parents[x]);
19                 return parents[x];
20             }
21 
22             public void union(int x, int y) {
23                 int rootX = find(x);
24                 int rootY = find(y);
25                 if (rootX == rootY) return;
26                 if (ranks[rootX] > ranks[rootY]) parents[rootY] = rootX;
27                 if (ranks[rootX] < ranks[rootY]) parents[rootX] = rootY;
28                 if (ranks[rootX] == ranks[rootY]) {
29                     parents[rootY] = rootX;
30                     ranks[rootY]++;
31                 }
32             }
33         }
34 
35 
36 //作者：a-fei-8
37 //链接：https://leetcode-cn.com/problems/redundant-connection/solution/yi-wen-zhang-wo-bing-cha-ji-suan-fa-by-a-fei-8/
38 //来源：力扣（LeetCode）
39 //著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
    主体代码
     1 int m, n;
 2 int[][] directions = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
 3 
 4 public void solve(char[][] board) {
 5     if (board == null || board.length == 0) return;
 6     m = board.length;
 7     n = board[0].length;
 8     int initValue = m * n + 1;
 9     UnionFindSet unionFindSet = new UnionFindSet(initValue);
10     int dummy = m * n;
11     for (int i = 0; i < m; i++) {
12         for (int j = 0; j < n; j++) {
13             if (board[i][j] == 'O') {
14                 if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
15                     unionFindSet.union(node(i, j), dummy);
16                 } else {
17                     for (int k = 0; k < directions.length; k++) {
18                         int nextI = i + directions[k][0];
19                         int nextJ = j + directions[k][1];
20                         if ((nextI > 0 || nextI < m || nextJ > 0 || nextJ < n) && board[nextI][nextJ] == 'O') {
21                             unionFindSet.union(node(i, j), node(nextI, nextJ));
22                         }
23                     }
24                 }
25             }
26         }
27     }
28     for (int i = 0; i < m; i++) {
29         for (int j = 0; j < n; j++) {
30             if (unionFindSet.find(node(i, j)) == unionFindSet.find(dummy)) {
31                 board[i][j] = 'O';
32             } else {
33                 board[i][j] = 'X';
34             }
35         }
36     }
37 }
38 
39 public int node(int i, int j) {
40     return i * n + j;
41 }
42 
43 //作者：a-fei-8
44 //链接：https://leetcode-cn.com/problems/redundant-connection/solution/yi-wen-zhang-wo-bing-cha-ji-suan-fa-by-a-fei-8/
45 //来源：力扣（LeetCode）
46 //著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

    2.冗余连接
    图传上来就没了，有毒，684题：冗余连接

    思路
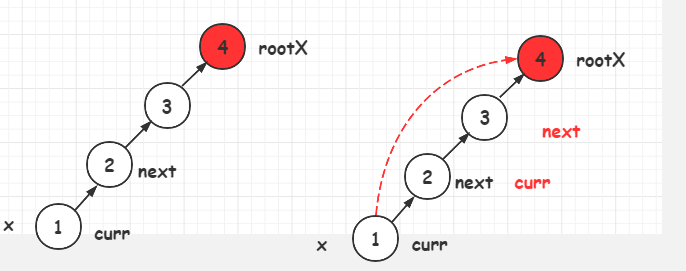
    判断节点第一次出现环的边edgeedge进行返回，如下图，当11的根节点是44的时候，从1->2->3->41−>2−>3−>4出现一条路径，大概[1,4][1,4]这个edgeedge进来后，发现11可以直接指向44，这时候出现了环，这条边是冗余边

     

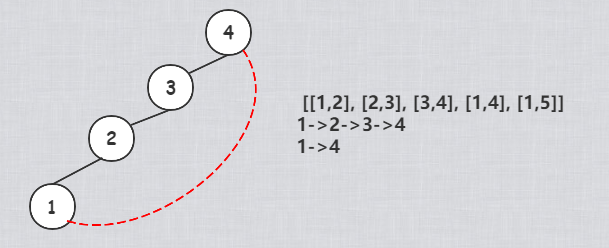
     1     int[] parents;
 2 
 3     public int[] findRedundantConnection(int[][] edges) {
 4         if (edges == null || edges.length == 0) return new int[]{0, 0};
 5         int n = edges.length + 1; //注意此处下标多放一个
 6         init(n);
 7         for (int[] edge : edges) {
 8             int x = edge[0], y = edge[1];
 9             if ((!union(x, y))) {//第二次出现了联通的边时，表示已经找到了
10                 return edge;
11             }
12         }
13         return new int[]{0, 0};
14     }
15     //初始化parents
16     public void init(int n) {
17         parents = new int[n];
18         for (int i = 0; i < n; i++) {
19             parents[i] = i;
20         }
21     }
22 
23     //递归版路径压缩，找到x的根节点
24     public int find(int x) {
25         if (x != parents[x]) {
26             parents[x] = find(parents[x]);
27         }
28         return parents[x];
29     }
30 
31     //改写union方法，第一次当x与y没有联通时，将其设置联通关系，返回ture
32     //第二次x和y的跟节点发现一致时，他们已经联通了，返回false
33     public boolean union(int x, int y) {
34         int rootX = find(x), rootY = find(y);
35         if (rootX == rootY) return false;
36         parents[rootX] = rootY;
37         return true;
38     }
39 
40 //作者：a-fei-8
41 //链接：https://leetcode-cn.com/problems/redundant-connection/solution/yi-wen-zhang-wo-bing-cha-ji-suan-fa-by-a-fei-8/
42 //来源：力扣（LeetCode）
43 //著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
    番外
     1 //非递归版路径压缩
 2 public int find(int x) {
 3     int rootX = x;
 4     while (rootX != parents[rootX]) {
 5         rootX = parents[rootX];
 6     }
 7     int curr = x;
 8     while (curr != rootX) {
 9         int next = parents[curr];
10         parents[curr] = rootX;
11         curr = next;
12     }
13     return rootX;
14 }
15 
16 //作者：a-fei-8
17 //链接：https://leetcode-cn.com/problems/redundant-connection/solution/yi-wen-zhang-wo-bing-cha-ji-suan-fa-by-a-fei-8/
18 //来源：力扣（LeetCode）
19 //著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

    思路差距

     本次思路较多且之间关系并不连贯，目测是有些拓扑学的理论，我对此所知甚少，待我先消化消化再写思路差距这一部分（才不是因为懒），四种思路都是上乘的思想，能熟练掌握必定大有用处。BFS跟DFS必然需要重点掌握，这是基础。

    技术差距

     这道题的首要技术差距就是如何在代码里体现路径点的移动问题了，大佬们所有的代码都是以如下的方式进行表达的：

    int[][] directions = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
    for (int[] d : directions) {
                       int ni = i + d[0], nj = j + d[1];
                       //判断(i,j) --> (ni,nj)的距离是否比当前的小距离小，如果是这点是有效的
                       if (inArea(ni, nj) && !vis[ni][nj] && Math.abs(heights[i][j] - heights[ni][nj]) <= max) {
                           vis[ni][nj] = true;
                           queue.add(new int[]{ni, nj});
                       }

     想不到之前在二维结构里竟然也能遇到表达不出来的窘境，代码功力还是不太够啊~
  • 相关阅读:
    【Linux】命令——基本命令
    正则表达式
    Letex
    Markdown
    文本编辑器Vim
    【Linux】集群
    【Linux】软件安装
    共线性synteny
    windows触控手势
    【Linux】bin结尾的安装包
  • 原文地址：https://www.cnblogs.com/monkiki/p/13899843.html
Copyright © 2020-2023  润新知