题目原文
50. Pow(x, n)
实现pow(x,n),即计算 x 的 n 次幂函数。
示例 1:
输入: 2.00000, 10 输出: 1024.00000
示例 2:
输入: 2.10000, 3 输出: 9.26100
示例 3:
输入: 2.00000, -2 输出: 0.25000 解释: 2的-2次方即1/2的平方
说明:
- -100.0 < x < 100.0
- n 是 32 位有符号整数,其数值范围是 [−231, 231 − 1] 。
尝试解答
估计读者朋友们看到这个题目都想骂人:“就这题目你还觉得难???就这?就这???”看位看官先别着急(就不能让我水一期吗?),这是字节跳动某次面试题目,要考察的地方不在于能否实现功能,而在于代码性能(运行速度、迭代次数等),先上我的代码:
class Solution: def myPow(self, x: float, n: int) -> float: return pow(x,n)
好的本次复盘结束,谢谢大家[x]
开个玩笑,下面是我的代码:
1 from functools import lru_cache 2 @lru_cache(maxsize=32) 3 class Solution: 4 def myPow(self, x: float, n: int) -> float: 5 if n==0: 6 return 1 7 if n<0: 8 return self.myPow(1/x,-n) 9 if n>0: 10 if n==1: 11 return x 12 elif n%2==1: 13 return x*self.myPow(x,(n-1)/2)*self.myPow(x,(n-1)/2) 14 elif n%2==0: 15 return self.myPow(x,n/2)*self.myPow(x,n/2)

因技术力不足,它超时了。。。但是思路跟大佬们的一样,使用的是二分加递归,具体思路如下图所示:
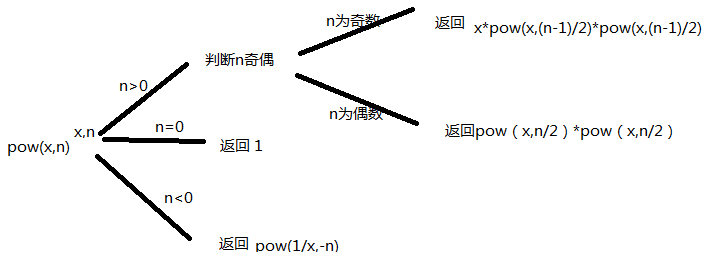
因为递归乘递归会消耗双倍的运算时间,之后运行时间会呈现级数增长趋势,因此稍微改了一下,下面是改良后的代码,运行通过:
1 from functools import lru_cache 2 @lru_cache(maxsize=32) 3 class Solution: 4 def myPow(self, x: float, n: int) -> float: 5 if n==0: 6 return 1 7 if n<0: 8 return self.myPow(1/x,-n) 9 if n>0: 10 if n==1: 11 return x 12 elif n%2==1: 13 a = self.myPow(x,(n-1)/2) 14 return x*a*a 15 elif n%2==0: 16 a = self.myPow(x,n/2) 17 return a*a

标准题解
思路一:
观赏一下大佬们的高技术力代码:
1 class Solution: 2 def myPow(self, x: float, n: int) -> float: 3 def quickMul(N): 4 ans = 1.0 5 # 贡献的初始值为 x 6 x_contribute = x 7 # 在对 N 进行二进制拆分的同时计算答案 8 while N > 0: 9 if N % 2 == 1: 10 # 如果 N 二进制表示的最低位为 1,那么需要计入贡献 11 ans *= x_contribute 12 # 将贡献不断地平方 13 x_contribute *= x_contribute 14 # 舍弃 N 二进制表示的最低位,这样我们每次只要判断最低位即可 15 N //= 2 16 return ans 17 18 return quickMul(n) if n >= 0 else 1.0 / quickMul(-n) 19 20 #作者:LeetCode-Solution 21 #链接:https://leetcode-cn.com/problems/powx-n/solution/powx-n-by-leetcode-solution/ 22 #来源:力扣(LeetCode) 23 #著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。




思路二:



1 class Solution: 2 def myPow(self, x: float, n: int) -> float: 3 if x == 0.0: return 0.0 4 res = 1 5 if n < 0: x, n = 1 / x, -n 6 while n: 7 if n & 1: res *= x 8 x *= x 9 n >>= 1 10 return res 11 12 #作者:jyd 13 #链接:https://leetcode-cn.com/problems/powx-n/solution/50-powx-n-kuai-su-mi-qing-xi-tu-jie-by-jyd/ 14 #来源:力扣(LeetCode) 15 #著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
思路差距
一、我一开始的思路还是最笨的,x一个一个得乘下去,得知最大递归深度远远超出限制后我改了思路,跟大佬的分治法的思路基本一致,但有一个地方需要注意:

这是比较细节的东西,积累下来积累下来~,还有就是不一定用到递归,递归确实会占用不少资源,但代码简洁性也是显而易见的,关于递归利弊的分析详见知乎https://www.zhihu.com/question/35255112,像二叉树这种的数据结构相关问题基本都是在用递归算法,当然也可以借助栈的辅助进行访问(这个我是完全不会。。大概以后会遇到吧)
二、从二进制角度分析的思路实在是高!这个没得说先记下来吧,估计后面的问题还会用到。虽然两种思路没那么相似,但细看两种思路的代码会发现对数据的处理过程几乎是一致的,那这两种思路是否可以看作本质上的同一种?幂操作跟二进制之间的数学关系还有待思考。
三、讲道理力扣中等难度的题目果然轻松很多,无论是思路复杂程度还是细节控制方面,思维量比起困难题都大幅下降,但里面知识也是不少的,还是应该注重基础多多积累。
技术差距
一、代码的熟练度和对递归的运用比起第二期更熟练了一些,希望后面能提高更多吧,但或许有时候可以多试试不同的方法解决同一问题?
二、分治思想是很早之前积累的成果,所以这次比较轻松地就用出来了,很明显这点积累还远远不够用,有种三板斧抡完就没招的意思,所以还是要积累更多的技巧,毕竟这些技巧都是被整个代码编写者人群反复优化反复使用的,必然比一个人在短时间内想出的点子成熟的多。
三、代码写得过于啰嗦冗长,这给人一种外行的感觉并且会降低代码的性能,应该学会在细节点跟代码简洁上找到平衡点,或者说简洁的代码也不一定不钻细节(还是我太菜),代码还是应该多写,写完自己精简一下。