写在前面
该系列主要事对指针网络在NER以及关系抽取系列取得的成果进行展示,并根据大佬们的笔记总结其中的优劣以及理论分析。
GlobalPointer
在之前的工作中,我们NER采用传统的LSTM+CRF,在各个字段指标也取得不错的效果,简单字段类似学历这种f1值均在95以上,复杂一点的比如行业专业等也在90以上;最终评估完全准确率(对一篇文档,所有字段均抽取正确算对)85以上。而基于当前模型也没有什么太好的优化方案,无非就是针对性补数据,后处理等等。基于此着手调研当前NER更好的方式,当然直接用BERT+CRF会取得比当前更好的效果,有不错的提升,但性能问题却很难解决,能做的就是对BERT进行蒸馏、剪枝,但其实效果并不能令人满意。
偶然之间(必然)看到了苏老师的GlobalPointer,遂进行了深入研究和探索,最终取得不错的结果,借助苏老师的模型,完全准去率从85上升到91,在cpu测试单挑耗时不到17ms,不得不说是性能和指标双重达标。(注意:此处采用的BERT是四层的BERT,接用网上teacher-student训练的四层模型结果来做的,完整的BERT完全准确率高达96,耗时未测,我偷懒了)
下面简单介绍一下优雅与性能并存的GlobalPointer是怎么回事!!!
利用全局归一化思路进行实体识别,兼容了嵌套实体和非嵌套实体,设计理论比CRF更合理,训练过程中也不需要想CRF一样递归计算分母,预测的时候也不需要动态规划,完全并行,理想情况瞎时间复杂度\(\color{blue}{O(1)}\)。
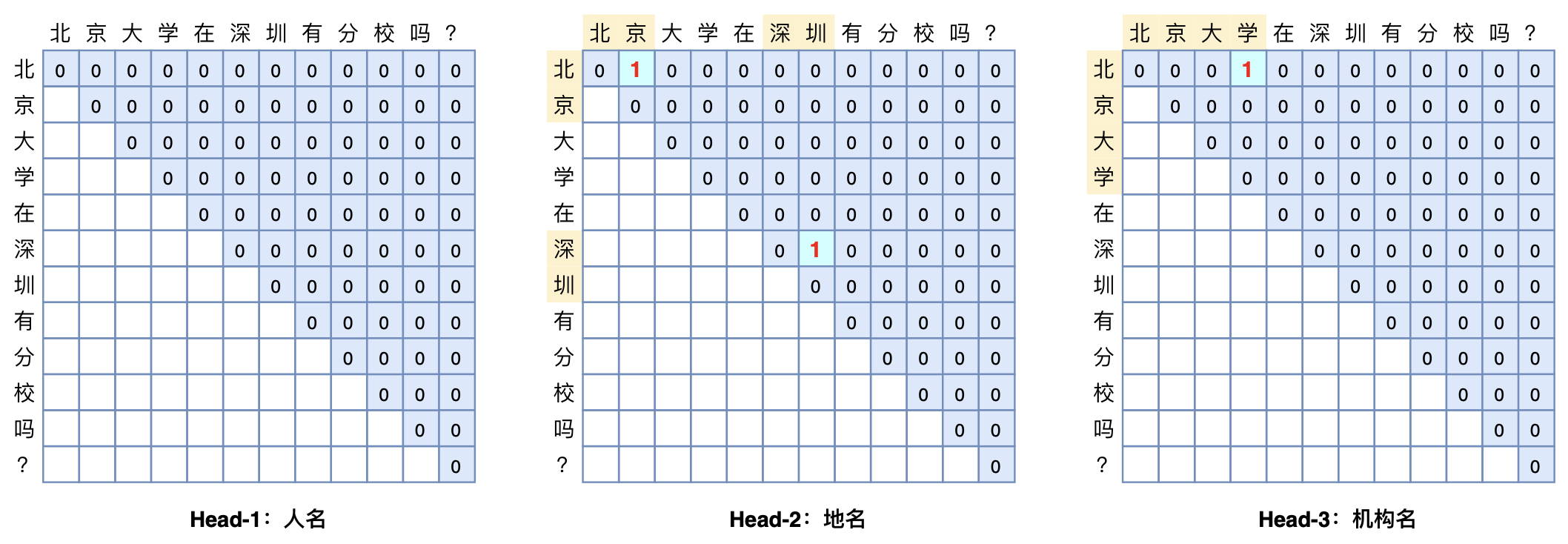
\(\color{red}{Pointer\ Network 与 GlobalPointer区别}\)
- Pointer Network一般采用两个模块分别识别实体的首和尾,而GlobalPointer将首位是为一个整体去进行判断,如上图,因此更具有“全局观”。
基本思路
假设我们要对一个文本长度为n的文本进行实体识别,而理论上我们识别的实体是连续的,并且最大长度可以为n,由此可以得出最大候选实体个数有\(\color{blue}{n(n+1)/2}\)个;问题就转换为我们从这些候选中挑选出真实的实体,就变成了m个关系从候选中选k的多标签分类问题。
这里可以发现一个问题就是复杂度为\(\color{blue}{O(n^2)}\),但这其实是空间上的复杂度,在时间上完全可以并行,可以降到\(\color{blue}{O(n)}\)。
数学形式
长度为n的t输入经过编码后得到向量序列\(\color{blue}{h_1,h_2,...h_n}\),通过变换\(\color{blue}{q_{i,\alpha}=w_{q,\alpha}h_i+b_{q,\alpha}}\)和\(\color{blue}{k_{i,\alpha}=w_{k,\alpha}h_i+b_{k,\alpha}}\),可以得到序列向量\(\color{blue}{[q_{1,\alpha},q_{2,\alpha},...,p_{n,\alpha}]}\)和\(\color{blue}{[k_{1,\alpha},k_{2,\alpha},...,k_{n,\alpha}]}\),是识别第\(\color{blue}{\alpha}\)种类型实体所用的向量序列。此时可以定义:
上面就是\(\color{blue}{\alpha}\)类型实体\(\color{blue}{t_{[i:j]}}\)从i到j的打分。这里可以看出,其实就是Multi-Head Attention的一个简化版,少了V的相关运算。
位置编码
理论上公式(1)已经足够了,但实际训练中由于预料不足表现往往差强人意,究其原因是少了一些相对位置信息,在苏老师的实验中,加不加相对位置信息,指标差距近30%以上。
没有位置信息会导致如何呢?我们可以举个简单的例子,比如:北京巴拉巴拉上海巴拉拉吧广东,假设我们识别地名,由于GlobalPointer对句子的长度以及位置信息都不敏感,那么就有可能出现北京巴拉巴拉上海识别为地点。但是有了职位信息就会解决这个问题,从而区分出真正的实体。
关于位置编码一直想研究一下各种不同的位置编码的区别以及优劣,但苦苦没有开始,再次立个flag吧。下篇就写它,是的,已经立完了。直接说苏老师在里面用了RoPE旋转式位置编码,它其实就是一个变换矩阵\(\color{blue}{R_i}\),满足\(\color{blue}{R_i^TR_j=R{j-i}}\),这样应用到公式(1)的q,k中,得到如下:
这样就显式的往\(\color{blue}{s_\alpha(i,j)}\)里面注入了相对位置信息。
上述内容,从基本思路到数学形式、位置编码就基本说完了GlobalPointer的原理及模型表示。下面说说优化。
损失函数
从上面可以看出,最终打分函数相当于\(\color{blue}{\alpha}\)个\(\color{blue}{n(n+1)/2}\)类个二分类问题,相当于对每个类型的实体候选有\(\color{blue}{n(n+1)/2}\)这么多个,每个候选相当于做一个二分类问题,很明显,最后会存在严重的类别不平衡问题。
参考2《将“softmax+交叉熵”推广到多标签分类问题》,里面提到的方式就是单目标多分类的交叉熵的推广,适合总数很大但目标标签很少的场景。公式如下:
其中\(\color{blue}{P_\alpha}\)是该样本的所有类型为\(\color{blue}{\alpha}\)的实体的收尾集和,\(\color{blue}{Q_\alpha}\)是该样本所有非实体或者类型非\(\color{blue}{\alpha}\)的实体的收尾集和,注意我们只需要考虑\(\color{blue}{i\leq j}\)的组合,即:
而在解码阶段,所有满足\(\color{blue}{s_\alpha(i,j)\gt0}\)的片段\(\color{blue}{t_{[i:j]}}\)都被视为类型\(\color{blue}{\alpha}\)的实体输出。可以看出,解码的过程是极其简单的,并且充分并行下解码效率就是\(\color{blue}{O(1)}\)!。
实验结果
展示在CMeEE(嵌套任务)数据上的实验结果。
| 验证集F1 | 测试集F1 | 训练速度 | 预测速度 | |
|---|---|---|---|---|
| CRF | 63.81% | 64.39% | 1x | 1x |
| GP | 64.84% | 65.98% | 1.52x | 1.13x |
与CRF对比[纯copy]
假设序列标注标签数为k,那么逐帧softmax和crf的区别在于:\(\color{red}{前者将序列标注堪称n个k分类问题,后者将序列标注堪称1个k^n分类问题}\)。这也说明了逐帧softmax和crf用于NER时的理论上的缺点。 逐帧softmax将序列标注看成是n个k分类问题,那是过于宽松了,因为某个位置上的标注标签预测对了,不代表实体就能正确抽取出来了,起码有一个片段的标签都对了才算对;相反,CRF将序列标注看成是1个\(\color{blue}{k^n}\)分类问题,则又过于严格了,因为这意味着它要求所有实体都预测正确才算对,只对部分实体也不给分。虽然实际使用中我们用CRF也能出现部分正确的预测结果,但那只能说明模型本身的泛化能力好,CRF本身的设计确实包含了“全对才给分”的意思。
所以,CRF在理论上确实都存在不大合理的地方,而相比之下,GlobalPointer则更加贴近使用和评测场景:它本身就是以实体为单位的,并且它设计为一个“多标签分类”问题,这样它的损失函数和评价指标都是实体颗粒度的,哪怕只对一部分也得到了合理的打分。因此,哪怕在非嵌套NER场景,GlobalPointer能取得比CRF好也是“情理之中”的。