竞争神经网络学习
竞争型神经网络是基于无监督学习(Unsupervised learning)方法的神经网络的一种重要类型,它经常作为基本的网络形式,构成其它一些具有自组织能力的网络,如自组织映射网络(SOM)、自适应共振理论网络、学习向量量化网络等。
生物神经网络存在一种侧抑制的现象,即一个神经细胞兴奋后,通过它的分支会对周围其他神经细脑产生抑制,这种抑制使神经细胞之间出现竞争:在开始阶段,各神经元对相同的输入具有相同的响应机会,但产生的兴奋程度不同,其中兴奋最强的一个神经细胞对周围神经细胞的抑制作用也最强,从而使其它神经元的兴奋得到最大程度的抑制,而兴奋最强的神经细胞却“战胜”了其它神经元的抑制作用脱颖而出,成为竞争的胜利者,并因为获胜其兴奋的程度得到进一步加强,正所谓“成者为王,败者为寇”。
一、竞争型神经网络结构模型:
竞争型神经网络只有两层(输入层和核心输出层),如图所示:
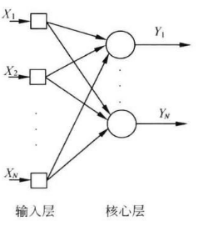
竞争型神经网络结构
在竞争神经网络中,输出层又被称为核心层。在一次计算中,只有一个输出神经元获胜,获胜的神经元标记为1,其余神经元标记为0。起初,输入层到核心层的权值是随机给定的,因此每个核心层神经元获胜的概率相同,但最后会有一个兴奋最强的神经元。兴奋最强的神经元“战胜”了其他神经元,在权值调制中其兴奋程度得到进一步加强,而其他神经元则保持不变。竞争神经网络通过这种竞争学习的方式获取训练样本的分布信息,每个训练样本都对应一个兴奋的核心层神经元,也就是对应一个类别,当有新样本输入时,就可以根据兴奋的神经元进行模式分类。
二、关于输入层到竞争层有几种不同的计算方法:
1、计算输入向量和权值距离的负数,然后加上一个阈值,结果大的那个神经元获胜,获胜为1,其他为0,然后调节获胜神经元对应的阈值。以下为步骤:
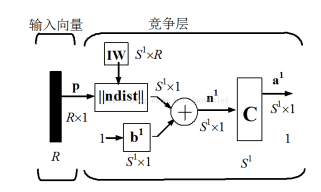
可以看出竞争型神经网络为单层网络。||ndist|| 的输入为输入向量p和输入权值向量IW,其输出为(S1*1)的列向量,列向量中的每个元素为输入向量p和输入权值向量IW距离的负数(negative),在神经网络工具箱中以距离函数negdist进行计算。
n1为竞争层传输函数的输入,其值为输入向量p和输入权值向量IW距离的负数与阈值b1之和。如果所有的阈值向量为0,则当输入向量p和输入权值向量IW相等时,n1为最大值0。
对于n1中最大的元素,竞争层传输函数输出1(即竞争的“获胜者”输出为1),而其它元素均输出0。如果所有的阈值向量为0,则当神经元的权值向量最接近输入向量时,它在n1各元素中的负值最小,而值最大,从而赢得竞争,对应的输出为1。
2、竞争型神经网络的学习
(1)Kohonen 权值学习规则
竞争型神经网络按Kohonen学习规则对获胜神经元的权值进行调整。假若第i个神经元获胜,则输入权值向量的第i行元素(即获胜神经元的各连接权)按下式进行调整,而其他神经元的权值不变。
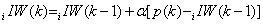
Kohonen学习规则通过输入向量进行神经元权值的调整,因此在模式识别的应用中是很有用的。通过学习,那些最靠近输入向量的神经元权值向量被修正,使之更靠近,其结果是获胜的神经元在下一次相似的输入向量出现时,获胜的可能性会更大;而对于那些相差很远的输入向量,获胜的可能性将变得很小。
这样,当经过越来越多的训练样本学习后,每一个网络层中的神经元的权值向量很快被调整为最接近某一类输入向量的值。最终的结果是,如果神经元的数量足够多,则具有相似输入向量的各类模式作为输入向量时,其对应的神经元输出为1;而对于其它模式的输入向量,其对应的神经元输出为0。所以,竞争型网络具有对输入向量进行学习分类的能力。
(2)阈值学习规则
在竞争型神经网络中,有可能某些神经元始终无法赢得竞争,其初始值偏离所有样本向量,因此无论训练多久都无法成为获胜神经元。这种神经元称为“死神经元”。
为了解决死神经元的问题,可以给很少获胜的神经元以较大的阈值,使其在输入向量与权值相似性不太高的情况下也有可能获胜;而对于那些经常获胜的神经元则给以较小的阈值。在实现时,通过计算神经元输出为1的百分比,因此越经常获胜的神经元,其输出向量的平均值越大,而死神经元输出向量的平均值为零。
阈值学习规则有如下两点好处:
a、有效解决了“死神经元”问题
b、经常获胜的神经元,其阈值不断下降,获胜的概率逐渐降低。系统强行降低这类神经元的输入响应空间,输入向量必须与权值很相似时神经元才会响应,而对于从未获胜的神经元来说,则不必如此相似。当输入空间的一个区域包含很多输入向量时,输入向量密度大的区域将吸引更多的神经元,导致更细的分类,而输入向量稀疏处则恰好相反。
阈值学习规则的运行过程就像人类的“同情”弱者一样,体现人的“良心”,在MATLAB中阈值学习规则由learncon函数实现。
三、竞争型神经存在的问题
对于模式样本本身具有较明显的分类特征,竞争型神经网络可以对其进行正确的分类,网络对同一类或相似的输入模式具有较稳定的输出响应。但也存在一些问题:
(1)当学习模式样本本身杂乱无章,没有明显的分类特征时,网络对输入模式的响应呈现振荡的现象,即对同一类输入模式的响应可能激活不同的输出神经元,从而不能实现正确的分类。当各类模式的特征相近时,也会出现同样的状况。
(2)在权值和阈值的调整过程中,学习率的选择在学习速率和稳定性之间存在矛盾,而不象前面我们介绍的其它学习算法,可以在刚开始时采用较大的学习率,而在权值和阈值趋于稳定时,采用较小的学习率。而竞争型神经网络当增加新的学习样本时,权值和阈值可能需要比前一次更大的调整。
(3)网络的分类性能与权值和阈值的初始值、学习率、训练样本的顺序、训练时间的长短(训练次数)等都有关系,而又没有有效的方法对各种因素的影响加以评判。
(4)在MATLAB神经网络工具箱中,以trainr函数进行竞争型神经网络的训练,用户只能限定训练的最长时间或训练的最大次数,以此终止训练,但终止训练时网络的分类性能究竟如何,没有明确的指标进行评判。