1. 综述
1.1 Cover和Hart在1968年提出了最初的邻近算法
1.2 分类(classification)算法|回归算法,这里讨论的是分类算法
1.3 输入基于实例的学习(instance-based learning), 懒惰学习(lazy learning)
2.1 步骤
为了判断未知实例的类别,以所有已知类别的实例作为参照
选择参数K
计算未知实例与所有已知实例的距离
选择最近K个已知实例
根据少数服从多数的投票法则(majority-voting),让未知实例归类为K个最邻近样本中最多数的类别
2.2 细节:
关于K
关于距离的衡量方法:
2.2.1 Euclidean Distance 定义
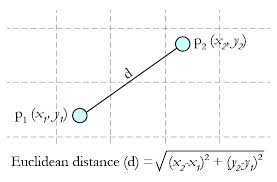
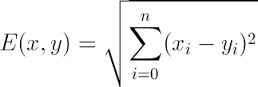
其他距离衡量:余弦值(cos), 相关度 (correlation), 曼哈顿距离 (Manhattan distance)
2.3 举例
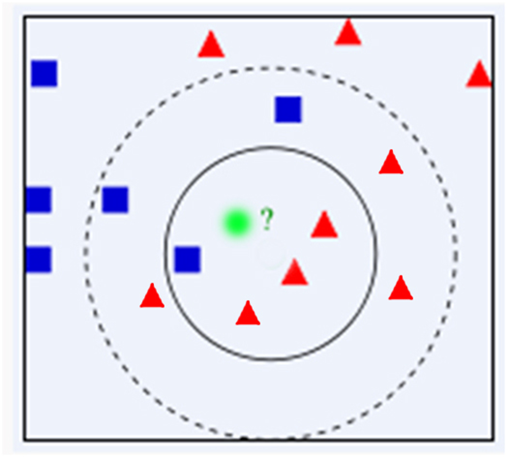
3. 例子

未知电影属于什么类型?
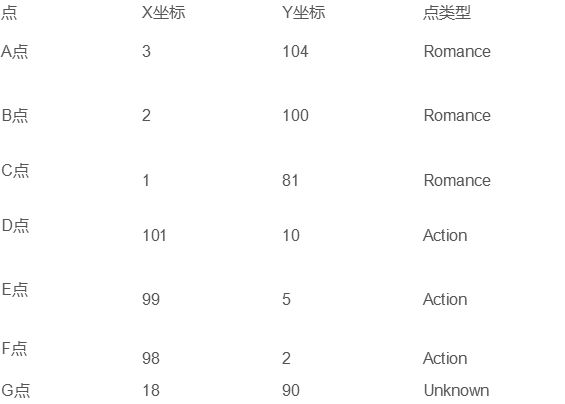
4、python代码实现
利用Python的机器学习库sklearn: SkLearnExample.py
import csv
import random
import math
import operator
def loadDataset(filename, split, trainingSet = [], testSet = []):
'''
导入数据
:param filename:
:param split: 将数据总集以split为界限 分成训练集和测试集
:param trainingSet:
:param testSet:
:return:
'''
with open(filename, 'rt') as csvfile: # 以逗号为分隔符
lines = csv.reader(csvfile) # 读取所有行
dataset = list(lines)
for x in range(len(dataset)-1):
for y in range(4):
dataset[x][y] = float(dataset[x][y])
if random.random() < split:
trainingSet.append(dataset[x])
else:
testSet.append(dataset[x])
def euclideanDistance(instance1, instance2, length):
'''
计算euclideanDistance
:param instance1:
:param instance2:
:param length: 维度
:return:
'''
distance = 0
for x in range(length):
distance += pow((instance1[x]-instance2[x]), 2)
return math.sqrt(distance)
def getNeighbors(trainingSet, testInstance, k):
'''
返回最近的k个邻居
:param trainingSet: 训练集
:param testInstance: 一个测试实例
:param k: 参数k
:return:
'''
distances = []
length = len(testInstance)-1
for x in range(len(trainingSet)):
#testinstance
dist = euclideanDistance(testInstance, trainingSet[x], length)
distances.append((trainingSet[x], dist))
#distances.append(dist)
distances.sort(key=operator.itemgetter(1))
neighbors = []
for x in range(k):
neighbors.append(distances[x][0])
return neighbors
def getResponse(neighbors):
'''
以距离排序,返回最近的几个点
:param neighbors:
:return:
'''
classVotes = {}
for x in range(len(neighbors)):
response = neighbors[x][-1]
if response in classVotes:
classVotes[response] += 1
else:
classVotes[response] = 1
sortedVotes = sorted(classVotes.items(), key=operator.itemgetter(1), reverse=True) # python3 里的.items()返回的是列表,.iteritems()返回的是一个迭代器
return sortedVotes[0][0]
def getAccuracy(testSet, predictions):
'''
预测值和实际值的准确率
:param testSet:
:param predictions:
:return:
'''
correct = 0
for x in range(len(testSet)):
if testSet[x][-1] == predictions[x]:
correct += 1
return (correct/float(len(testSet)))*100.0
def main():
#prepare data
trainingSet = []
testSet = []
split = 0.67
loadDataset(r'irisdata.txt', split, trainingSet, testSet)
print('Train set: ' + repr(len(trainingSet)))
print('Test set: ' + repr(len(testSet)))
#generate predictions
predictions = []
k = 3
for x in range(len(testSet)):
# trainingsettrainingSet[x]
neighbors = getNeighbors(trainingSet, testSet[x], k)
result = getResponse(neighbors)
predictions.append(result)
print ('>predicted=' + repr(result) + ', actual=' + repr(testSet[x][-1]))
accuracy = getAccuracy(testSet, predictions)
print('Accuracy: ' + repr(accuracy)+ '%')
if __name__ == '__main__':
main()
5. 算法优缺点
5.1 算法优点
简单
易于理解
容易实现
通过对K的选择可具备丢噪音数据的健壮性
5.2 算法缺点
需要大量空间储存所有已知实例
算法复杂度高(需要比较所有已知实例与要分类的实例)
当其样本分布不平衡时,比如其中一类样本过大(实例数量过多)占主导的时候,新的未知实例容易被归类为这个主导样本,因为这类样本实例的数量过大,但这个新的未知实例实际并木接近目标样本