Description
设 (d(x)) 为 (x) 的约数个数,给定 (n,m),求 (sum_{i=1}^nsum_{j=1}^md(ij)),(n,m,T le 5 imes 10^4)
Solution
重要结论如黑色式子所示,其余部分为套路性的反演推导
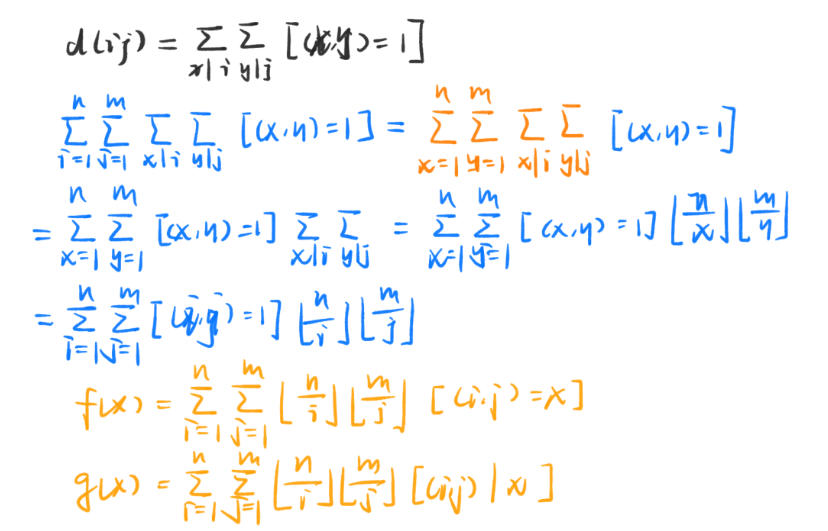

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 50005;
const int MAXN = 50005;
bool isNotPrime[MAXN + 1];
int mu[MAXN + 1], phi[MAXN + 1], primes[MAXN + 1], cnt, h[MAXN+1];
inline void euler() {
isNotPrime[0] = isNotPrime[1] = true;
mu[1] = 1;
phi[1] = 1;
for (int i = 2; i <= MAXN; i++) {
if (!isNotPrime[i]) {
primes[++cnt] = i;
mu[i] = -1;
phi[i] = i - 1;
}
for (int j = 1; j <= cnt; j++) {
int t = i * primes[j];
if (t > MAXN) break;
isNotPrime[t] = true;
if (i % primes[j] == 0) {
mu[t] = 0;
phi[t] = phi[i] * primes[j];
break;
} else {
mu[t] = -mu[i];
phi[t] = phi[i] * (primes[j] - 1);
}
}
}
for(int i=1;i<=MAXN;i++) mu[i]+=mu[i-1];
}
int calch(signed x) {
signed l=1;
int ans=0;
while(l<=x) {
signed r=x/(x/l);
ans+=1ll*(r-l+1)*(x/l);
l=r+1;
}
return ans;
}
int solve(int n,int m) {
if(n==0 || m==0) return 0;
int ans=0,l=1,r=0;
if(n>m) swap(n,m);
while(l<=n) {
r=min(n/(n/l),m/(m/l));
ans+=(mu[r]-mu[l-1])*h[n/l]*h[m/l];
l=r+1;
}
return ans;
}
signed main() {
euler();
int t,a,b,c,d,k;
ios::sync_with_stdio(false);
cin>>t;
for(int i=1;i<=5e4;i++) h[i]=calch(i);
while(t--) {
int n,m;
cin>>n>>m;
cout<<solve(n,m)<<endl;
}
}