Luogu P1169 [ZJOI2007]棋盘制作

gate

悬线法

用于求极大子矩阵

(l[i][j]：(i,j))能扩展到的最左边的点
(r[i][j]：(i,j))能扩展到的最右边的点
(up[i][j]：(i,j))能扩展到的最上边的长度

预处理：（如果合法）
(l[i][j] = l[i][j-1])
(r[i][j] = r[i][j+1])

状态转移方程：（如果合法）
(l[i][j] = max(l[i][j],l[i-1][j]))
(r[i][j] = min(r[i][j],r[i-1][j]))
(up[i][j] = up[i-1][j]+1)

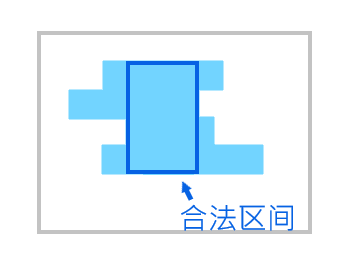
也就是，如果这一点能从上面的点转移过来，则左右端点取较小的。
像这样：

代码如下

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#define MogeKo qwq
using namespace std;

const int maxn = 2005;
int n,m,wid,ans1,ans2;
int a[maxn][maxn],l[maxn][maxn],r[maxn][maxn],up[maxn][maxn];

int main() {
	scanf("%d%d",&n,&m);
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= m; j++) {
			scanf("%d",&a[i][j]);
			l[i][j] = r[i][j] = j;
			up[i][j] = 1;
		}
	for(int i = 1; i <= n; i++)
		for(int j = 2; j <= m; j++)
			if(a[i][j] != a[i][j-1])
				l[i][j] = l[i][j-1];
	for(int i = 1; i <= n; i++)
		for(int j = m-1; j >= 1; j--)
			if(a[i][j] != a[i][j+1])
				r[i][j] = r[i][j+1];
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= m; j++) {
			if(i > 1 && a[i][j] != a[i-1][j]) {
				l[i][j] = max(l[i][j],l[i-1][j]);
				r[i][j] = min(r[i][j],r[i-1][j]);
				up[i][j] = up[i-1][j]+1;
			}
			wid = min(up[i][j],r[i][j]-l[i][j]+1);
			ans1 = max(ans1,wid*wid);
			ans2 = max(ans2,up[i][j]*(r[i][j]-l[i][j]+1));
		}
	printf("%d
%d",ans1,ans2);
	return 0;
}