NOIP之前,我绝对不学网络流。
——我
网络流可以解决这样一类问题:给定一个有向图,每条边有一个流量上限,求从源点到汇点所能运输的最大流量。
解决这类问题的一种算法叫做$dinic$。
一些性质
对于任意一个时刻,设c(u,v)为容量,f(u,v)为实际流量,则整个图G的流网络满足3个性质:
- 容量限制:对任意u,v∈V,f(u,v)≤c(u,v)。
- 反对称性:对任意u,v∈V,f(u,v) = -f(v,u)。从u到v的流量一定是从v到u的流量的相反值。
- 流守恒性:对任意u,若u不为S或T,一定有∑f(u,v)=0,(u,v)∈E。即u到相邻节点的流量之和为0,因为流入u的流量和u点流出的流量相等。
原理
假设存在一个有一些流但没有达到最大流的网络,如果能找到一条路径,使总流量增加,这样的路径被称为增广路。
反过来说,如果图中不存在增广路,那么这一定是网络最大流。
$dinic$算法就是一个不断寻找增广路的过程。
然而,这个结论可以很容易举出反例:
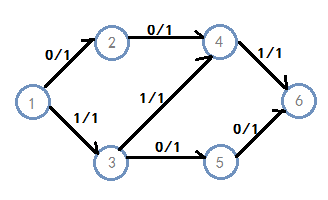
这是这个网络中的流的一种方式。它已经没有增广路了,但是,显然,它不是最优的。
那么,假设程序已经选择了这种方式,应该怎么办?这时候就需要引入反向边的概念。
一条正常的边流了多少,它的反向边的容量就增加多少。反向边初始容量为0。
那么,加上反向边,就得到了这样的一张图:
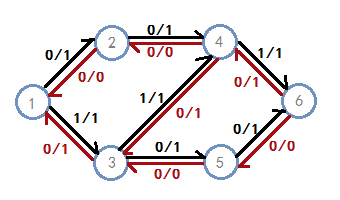
在这张图上再次寻找增广路,可以得到
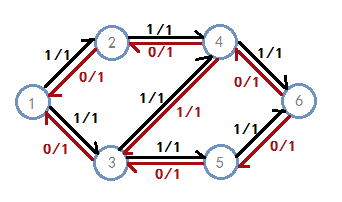
这样就得到了最大流。它和这样的流的方式是等价的
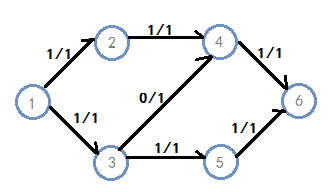
不难发现,反向边的作用就在于使流错了的边再流回去。
实现
$dinic$算法的流程可以概括为:
- bfs检查是否有增广路。若没有,则已达到最大流,程序结束。
- dfs找到一条增广路,将增加的流量计入答案。
- 返回1。
需要定义这些变量:
int dis[]; //从源点到这一点的距离(经过的边数) int cur[]; //走到这一点后,下一个可能找到增广路的边
cur[]的意义将在$dfs$的部分详细解释。
$dinic()$
根据上述流程,可以得到这样的代码
void dinic() { while(bfs()) { for(int i = 1; i <= n; i++) cur[i] = head[i]; ans += dfs(s,INF); } }
$bfs()$
想要找到增广路,需要检查每一条边剩余的容量w[i]能不能组成一条从s到t的通路。
在寻找的过程中,可以处理出最短路,即使找到了t,也不退出while循环。
和普通的$bfs$类似,首先将所有点到源点s的距离dis[]设置为-1,表示未访问过。
源点s本身的dis[]设置为0,并将s压入队列q。
每次弹出队首,检查它所连的边能到达的每一个点v。
若v未被访问过,且(u,v)还有剩余的流量(dis[v] == -1 && w[i]),说明(u,v)是一条可行的道路,将v压入队列。
如果搜索到了汇点t(dis[t]≠-1),说明有增广路,返回true。否则返回false。
bool bfs() { memset(dis,-1,sizeof(dis)); queue <int> q; dis[s] = 0; q.push(s); while(!q.empty()) { int u = q.front(); q.pop(); for(int i = head[u]; i != -1; i = nxt[i]) { int v = to[i]; if(dis[v] == -1 && w[i]) { dis[v] = dis[u] + 1; q.push(v); } } } if(dis[t] == -1) return false; return true; }
$dfs()$
dfs中每次传递两个变量:当前点u,当前流flow。用sum记录找到的增广路的总量。
检查u所连的边能到达的每一个点v。
for(int &i = cur[u]; i != -1; i = nxt[i])
注意,高亮部分和平时有一点不同,可以每次使到达的点的cur[u]改为nxt[i]。
也就是说,如果我们已经试过了这条边,那么它在这次搜索中一定不会再次成为增广路了。
下一次经过这一点时,直接从它的下一条边nxt[i]开始尝试即可。
这样可以比head[]→nxt[]→nxt[]→……节省一些时间。
在$dinic()$中,每次$bfs$后,将cur[]的初始值设置为head[]。
这个操作叫做当前弧优化。
如果v在这次bfs找到的最短路上,且(u,v)还有剩余的流量(dis[v] == dis[u]+1 && w[i]),说明(u,v)是一条可行的道路。
递归$dfs$点v。如果边(u,v)的剩余流量w[i]小于当前流量flow,那么最多就只能流w[i]而不是flow,下传的flow应该改为w[i],即dfs(v,min(flow,w[i]))。
如果找到汇点t,则说明找到了一条增广路,当前的flow则为增广的流量。回溯,记这个返回值为ff。
u之前的点的剩余容量都减小了ff,即flow -= f;总流量sum增加ff。
同时,当前边的容量w[i]减小ff,反向边的容量w[i^1]增加ff。
如果flow减ff等于0了,那么就可以跳出for循环。
注意,在建边时,如果从偶数开始,那么i的反向边就可以用i^1表示。
例如,第一条边0,反向边1;第二条边2(10),反向边3(11)。
当然,所有head[]的初值就要设置为-1;在for循环枚举边时,边界条件就为i != -1。
如果dfs结束时,sum的值为0,则说明没有找到增广路。那么,这次搜索中一定不会在以后找到一条经过u点的增广路。为了防止再次找到u点,将dis[u]改为0。
最后返回sum。
int dfs(int u,int flow){ if(u == t) return flow; int sum = 0; for(int &i = cur[u];i != -1;i = nxt[i]){ int v = to[i]; if((dis[v] == dis[u]+1) && w[i]){ int ff = dfs(v,min(flow,w[i])); flow -= ff; sum += ff; w[i] -= ff; w[i^1] += ff; if(!flow) break; } } if(!sum) dis[u] = -1; return sum; }
是不是很短!
完整代码如下

#include<cstdio> #include<iostream> #include<cmath> #include<cstring> #include<queue> #define MogeKo qwq using namespace std; const int maxn = 2e5+10; const int INF = 0x3f3f3f3f; int n,m,s,t,x,y,z,ans,cnt; int head[maxn],to[maxn],nxt[maxn],w[maxn]; int cur[maxn],dis[maxn]; void add(int x,int y,int z) { to[cnt] = y; nxt[cnt] = head[x]; head[x] = cnt; w[cnt++] = z; } bool bfs() { memset(dis,-1,sizeof(dis)); queue <int> q; dis[s] = 0; q.push(s); while(!q.empty()) { int u = q.front(); q.pop(); for(int i = head[u]; i != -1; i = nxt[i]) { int v = to[i]; if(dis[v] == -1 && w[i]) { dis[v] = dis[u] + 1; q.push(v); } } } if(dis[t] == -1) return false; return true; } int dfs(int u,int flow) { if(u == t) return flow; int sum = 0; for(int &i = cur[u]; i != -1; i = nxt[i]) { int v = to[i]; if((dis[v] == dis[u]+1) && w[i]) { int ff = dfs(v,min(flow,w[i])); flow -= ff; sum += ff; w[i] -= ff; w[i^1] += ff; if(!flow) break; } } if(!sum) dis[u] = -1; return sum; } void dinic() { while(bfs()) { for(int i = 1; i <= n; i++) cur[i] = head[i]; ans += dfs(s,INF); } } int main() { scanf("%d%d%d%d",&n,&m,&s,&t); memset(head,-1,sizeof(head)); for(int i = 1; i <= m; i++) { scanf("%d%d%d",&x,&y,&z); add(x,y,z),add(y,x,0); } dinic(); printf("%d",ans); return 0; }
