Luogu P1962 斐波那契数列（矩阵乘法模板）

传送门（其实就是求斐波那契数列....）

累了 明天再解释

做这道题需要一些关于矩阵乘法的基础知识。

1. 矩阵乘法的基础运算

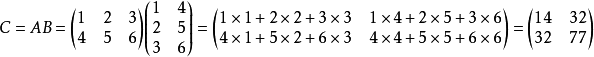
只有当矩阵A的列数等于矩阵B的行数时，A与B可以相乘（A的行数不一定等于B的列数）。

代码实现（重载运算符）：

struct matrix {
    int ma[2][3];
};
matrix operator * (const matrix &A,const matrix &B) {
    matrix C;
    for(int i = 0; i < 2; i++)
        for(int j = 0; j < 3; j++)
            for(int k = 0; k < 3; k++)
                C.ma[i][j] = C.ma[i][j] + A.ma[i][k] * B.ma[k][j];
    return C;
}

2. 单位矩阵

主对角线上的元素都为1，其余元素全为0的n阶矩阵称为n阶单位矩阵，记为或  

 

 

可以通过模拟推出，任何其他矩阵 * 单位矩阵 = 它本身。

 

回到这道题：

因为 f[i] = f[i-1] + f[i-2]，首先构造一个矩阵 [ f[i]  f[i-1] ]

它应该等于 [ f[i-1]  f[i-2] ] * A.

由于f[i] = f[i-1] *1 + f[i-2]*1，所以矩阵A的第一列应该都为1；

f[i-1] = f[i-1] *1 + f[i-2]*0，所以第二列为1和0；

即

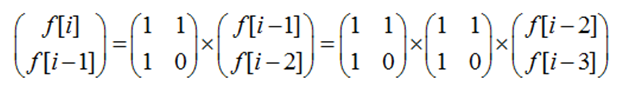
得到以下公式

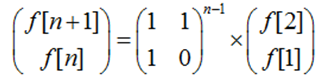
可以看出，求斐波那契数列即为求刚刚推导出的这个矩阵的n次幂；

这时就可以用快速幂来解决这道题了w

void quickpow(int b) {
    while(b) {
        if(b & 1) ans = ans * base;
        base = base * base;
        b >>= 1;
    }
}

int main() {
    if(n <= 2) {
        printf("1");
        return 0;
    }
    base.a[1][1] = base.a[1][2] = base.a[2][1] = 1;
    ans.a[1][1] = ans.a[1][2] = 1;
    quickpow(n - 2);
    printf("%d",ans.a[1][1]);
    return 0;
}

　　

（由于fibonacci数列的前两个数字=1已经给出，矩阵(f[2],f[1])即(1,1)是已知的，所以快速幂只要进行n-2次）

求的时候ans矩阵的第一个数即为答案。

 

 

• 一个小优化：当base自乘时，求出的数组刚好为

　　   

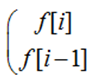
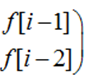
　　所以只要看n-1次的base[0][0]就可以了qwq（或者n次的base[0][1])

代码如下（我做的时候没有用重载运算符而是写了个函数来实现矩阵乘法的）

#include<cstdio>
#define ll long long
using namespace std;
const ll mod = 1000000007;

struct matrix {
    ll ma[2][2];
};

matrix ans;
ll n;

matrix mul(matrix A,matrix B) {
    matrix C;
    C.ma[0][0] = C.ma[0][1] = C.ma[1][0] = C.ma[1][1] = 0;
    for(int i = 0; i < 2; i++)
        for(int j = 0; j < 2; j++)
            for(int k = 0; k < 2; k++)
                C.ma[i][j] += A.ma[i][k] * B.ma[k][j] % mod;
    return C;
}

matrix quickpow(matrix A,ll n) {
    matrix B;
    B.ma[0][0] = B.ma[1][1] = 1;
    B.ma[0][1] = B.ma[1][0] = 0;
    while(n) {
        if(n&1)B = mul(A,B);
        A = mul(A,A);
        n >>= 1;
    }
    return B;
}

int main() {
    scanf("%lld",&n);
    matrix A;
    A.ma[0][0] = A.ma[0][1] = A.ma[1][0] = 1;
    A.ma[1][1] = 0;
    ans = quickpow (A,n);
    printf("%lld",ans.ma[0][1]%mod);
    return 0;
}