此算法灵感来自于apache内存池实现原理,不过读者如果没有看过apache内存池实现也无关系,因为本算法相对apache内存池算法更为简单而且易懂,个人认为某些场合也更为高效,或许真正到了apache服务器上性能不如,但是这套设计思想应该还是可以借鉴到更多场合的。
我们在调用malloc函数时,操作系统内部会查找一个所谓的空闲链表,当找到足够大的空闲空间时会将内存分割并返回一部分会用户,当然在很大的项目里面有可能会出现链表所有节点都找不到空闲空间的情形,此时操作系统便会不断搜索内存碎片,然后组合成一段足够大的空间并返回,如果此时还找不到便返回NULL。所以在new或者malloc调用后程序员有必要对申请的内存做是否为NULL的判断。而且在调用free后系统有可能还要合并内存产生额外开销,另外不断的malloc和free也会产生很多内存碎片并给操作系统管理内存带来很大的压力。所以说内存池算法在很多场合是非常必须的。
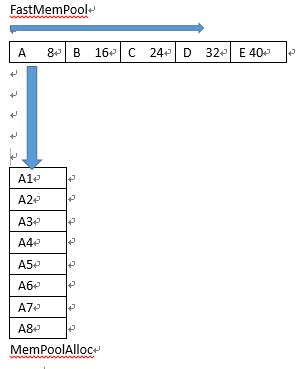
该内存池结构可以初步理解成一个二维数组,每个元素都是内存块。每个内存块都有一段附带的数据信息,代表这块内存在整个二维数组中的位置。申请和释放的时候可以根据附带信息直接找到内存块在内存池也就是这个二维数组中的位置。
以上A1到A8为例,假设整个内存池序列有n个,也就是A1到An,绝对会存在m(1<=m<=n),保证A1到Am为空闲状态,Am到An为被使用状态。
也就是说,如果内存池A1到An全部没有被使用,当申请内存时,只需要检查A1是否为空闲状态即可。有的可以返回,如果不是空闲,说明整个A序列内存都已经被占用了。当A1空闲,那么申请内存后将A1状态标记为被使用状态,然后将A1和An调换,此时保证内存池前n-1为未使用状态,n为使用状态。同样的道理,再次申请则将调整后的A1和A(n-1)调换,保证A1到A(n-2)为空闲状态,最后两个元素为被使用状态。
释放内存时,假设内存池序列是A1到Am为空闲,A(m+1)到An为被使用,而被使用的内存肯定是随机在m+1到n的某个元素,那么将其标记为未使用状态之后马上与m+1这个元素调换,此时保证A1到A(m+1)空闲,后A(m+2)到An为未使用。
所以说内存池中不管怎么申请释放或者调整,始终保证A1到Am空闲,之后的为被使用状态。如果中间有元素太长时间没被使用而释放,此时也需要根据这规则做调整。因为这样申请内存时不需要查表就可以找到元素,而释放内存时也能根据内存池管理数据结构中的外部和内部索引一步找到内存池中的位置,这也是该内存池高效的原因之一。
内存块附带的数据结构如下:
struct MemPoolData { unsigned int dwMemTrunkTicket; unsigned char chbIsMemTrunkUsed; unsigned char chOutIndex; unsigned char chInIndex; };
其中包含了该内存块是否被占用,上次使用时间戳以及在二维数组中的位置。
那么按照以上规则,假如说A1到A8都已经满员而且全都没有被使用,再次申请8字节内存时,首先检查A1这块内存是否已经被使用,如果被使用就无法申请。但是如果没有被使用则返回给程序,标记此内存已经被使用。然后将A8内存和A1调换,记录一个索引7,代表A1到A7没有被使用,A7以后的数据被使用了。同样的道理再次申请时仍然直接检查A1,因为没被使用则返回给程序,再将A1与A7调换,此时A1到A6没有被使用,A6到A8被使用了。释放内存时,假如说A1到A3未被使用而A4到A8被使用,释放的内存是A6,则将A6标记为未使用状态,将A4与A6调换即可。
另外如果申请和释放内存时,系统函数会锁住整个内存管理队列,而这套算法只会锁住当前大小序列,也就是说,申请8字节大小和申请16字节大小内存时不会产生锁竞争。因为8字节大小操作只是锁住A序列,16大小则是锁住图上的B序列。每个序列都有自己独立的锁。这也是高效快速的原因之一。以上就是申请和释放内存的基本思想,但是实际上向下的数组和自己实现和vector类似的容器,这样可以自动拓展,具体实现方法可以参考内存池源码。