Picture
题目链接
http://poj.org/problem?id=1177
Description
A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.
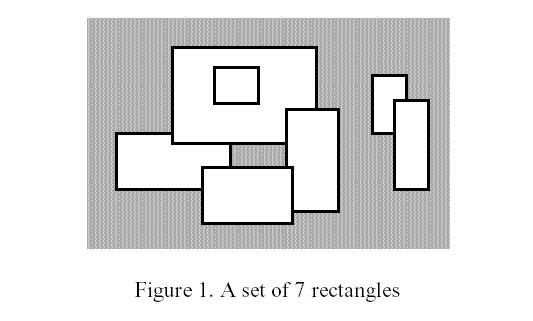
The corresponding boundary is the whole set of line segments drawn in Figure 2.
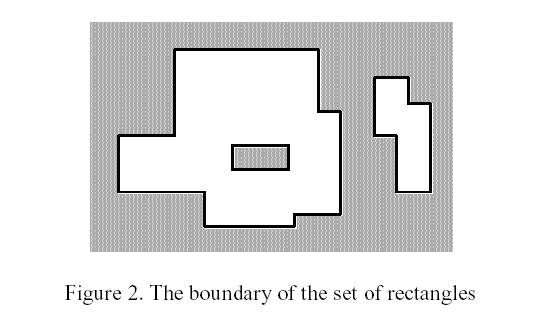
The vertices of all rectangles have integer coordinates.
Input
Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.
0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
Output
Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.
Sample Input
7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16
Sample Output
228
题意
经典入门题:求矩形周长并。
题解
我不知道别人怎么做的,我要扫四边,上下左右各扫一遍,具体说说从下往上扫,没扫到一条下边,就判断他下面有没有下边遮挡,减去遮挡长度就是这条下边所能贡献的有效长度;遇到上边,就把对应的下边去掉就好了。如果学过矩形面积并的话,应该很好理解。
代码
#include<cstdio>
#include<algorithm>
#include<string>
using namespace std;
#define ll long long
#define INF 0x7f7f7f7f
#define N 100050
ll ans;
int n,m,kth[N],cnt1,cnt2,num;
template<typename T>void read(T&x)
{
ll k=0; char c=getchar();
x=0;
while(!isdigit(c)&&c!=EOF)k^=c=='-',c=getchar();
if (c==EOF)exit(0);
while(isdigit(c))x=x*10+c-'0',c=getchar();
x=k?-x:x;
}
void read_char(char &c)
{while(!isalpha(c=getchar())&&c!=EOF);}
struct Query
{
int l,r,h,id;
bool operator<(const Query&e)const
{return h<e.h;};
}que[3][N];
struct Node{int l,r,lazy,sum;};
struct segmentTree
{
Node tr[N<<2];
void push_up(int x);
void bt(int x,int l,int r);
void update(int x,int l,int r,int tt);
int query(int x,int l,int r);
}seg;
void segmentTree::push_up(int x)
{
int len=kth[tr[x].r+1]-kth[tr[x].l];
if (tr[x].l<tr[x].r)tr[x].sum=tr[x<<1].sum+tr[x<<1|1].sum;
else tr[x].sum=0;
if (tr[x].lazy>0)tr[x].sum=len;
}
void segmentTree::bt(int x,int l,int r)
{
tr[x]={l,r,0,0};
if (l==r)return;
int mid=(l+r)>>1;
bt(x<<1,l,mid);
bt(x<<1|1,mid+1,r);
}
void segmentTree::update(int x,int l,int r,int tt)
{
if (l<=tr[x].l&&tr[x].r<=r)
{
tr[x].lazy+=tt;
push_up(x);
return;
}
int mid=(tr[x].l+tr[x].r)>>1;
if(l<=mid)update(x<<1,l,r,tt);
if(mid<r)update(x<<1|1,l,r,tt);
push_up(x);
}
int segmentTree::query(int x,int l,int r)
{
if (l<=tr[x].l&&tr[x].r<=r)return tr[x].sum;
if (tr[x].lazy>0)return kth[r+1]-kth[l];
int mid=(tr[x].l+tr[x].r)>>1,ans=0;
if (l<=mid)ans+=query(x<<1,max(tr[x].l,l),min(mid,r));
if (mid<r)ans+=query(x<<1|1,max(mid+1,l),min(tr[x].r,r));
return ans;
}
void solve(Query *que,int cnt)
{
seg.bt(1,1,num);
sort(que+1,que+cnt+1);
for(int i=1;i<=cnt-1;i++)
{
int l=lower_bound(kth+1,kth+num+1,que[i].l)-kth;
int r=lower_bound(kth+1,kth+num+1,que[i].r)-kth-1;
if (que[i].id==1)
ans+=1LL*(kth[r+1]-kth[l]-seg.query(1,l,r));
seg.update(1,l,r,que[i].id);
}
}
void work()
{
n=20050;
read(m);
for(int i=1;i<=m;i++)
{
int x1,y1,x2,y2;
read(x1); read(y1); read(x2); read(y2);
que[1][++cnt1]=Query{x1,x2,y1,1};
que[1][++cnt1]=Query{x1,x2,y2,-1};
que[2][++cnt2]=Query{y1,y2,x1,1};
que[2][++cnt2]=Query{y1,y2,x2,-1};
kth[++num]=x1;
kth[++num]=x2;
kth[++num]=y1;
kth[++num]=y2;
}
sort(kth+1,kth+num+1);
num=unique(kth+1,kth+num+1)-kth-1;//
solve(que[1],cnt1);
solve(que[2],cnt2);
for(int i=1;i<=cnt1;i++)que[1][i].h=-que[1][i].h,que[1][i].id=-que[1][i].id;
for(int i=1;i<=cnt2;i++)que[2][i].h=-que[2][i].h,que[2][i].id=-que[2][i].id;
solve(que[1],cnt1);
solve(que[2],cnt2);
printf("%lld
",ans);
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("aa.in","r",stdin);
#endif
work();
}