BZOJ 1043 下落的圆盘

Description

有n个圆盘从天而降，后面落下的可以盖住前面的。求最后形成的封闭区域的周长。看下面这副图, 所有的红色线条的总长度即为所求.

Input

n ri xi y1 ... rn xn yn

Output

最后的周长，保留三位小数

Sample Input

2
1 0 0
1 1 0

Sample Output

10.472

HINT

数据规模

n<=1000

这道题目很好嘴巴，但是写起来有点儿蛋疼。

首先求出每个圆盘被他上面的圆盘覆盖的圆心角的度数α，用(2π-α)*c/2π即每个圆盘的周长答案，最后累加一遍答案即可。

那么圆心角要怎么求呢？？？

算出两个圆的交点肯定是没戏的(我推了很久的公式，还是退错了)，后面想想，好像不用去求交点，可以直接用圆心角来计算区间。

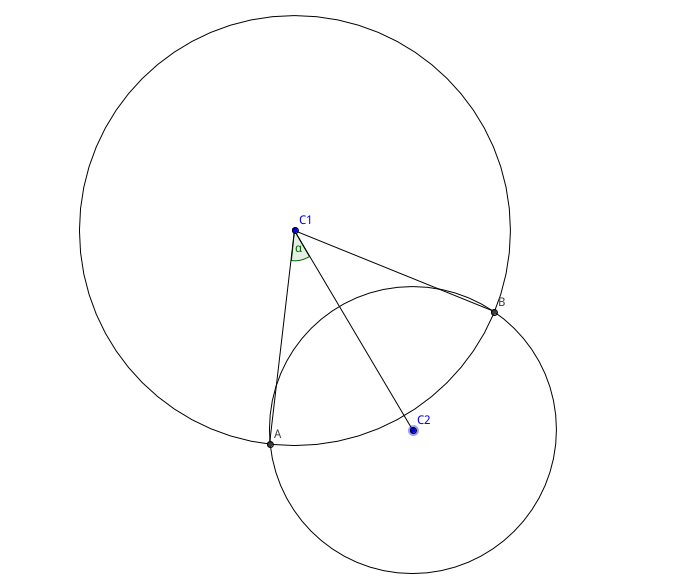
如图若两圆C1，C2有交点(C2覆盖C1)，则我们可以算出射线C1C2的极角θ。C1被C2所覆盖的圆心角的区间为[θ-α,θ+α]。但是注意，区间可能有越界的情况，比如说我们的区间是(-π,π]他的被覆盖的极角区间就是许多区间的并，但他可能和有[-1.2π，-0.7π]，这时我们需要将区间拆开进行处理。比如此例中，我们拆成[-π,-0.7π]与[0.8π,π]。

还有一种情况就是C1的圆心在C2中，α的值为其补角。(自己画画图)。

  1 #include<iostream>
  2 #include<cmath>
  3 #include<algorithm>
  4 #include<cstdio>
  5 #include<cstdlib>
  6 using namespace std;
  7 
  8 #define pi (3.1415926535)
  9 #define esp (1e-6)
 10 #define maxn 2010
 11 int n; double ans;
 12 
 13 inline bool equal(double a,double b) { return fabs(a - b) < esp; }
 14 
 15 inline double qua(double a) { return a * a; } 
 16 
 17 inline bool dd(double a,double b) { if (equal(a,b)) return true; return a >= b; } //>=
 18 
 19 inline bool xd(double a,double b) { if (equal(a,b)) return true; return a <= b; } //<=
 20 
 21 struct NODE{ double x,y; };
 22 struct angle
 23 {
 24     double a1,a2;
 25     friend inline bool operator < (angle a,angle b)
 26     {
 27         if (!equal(a.a1,b.a1)) return xd(a.a1,b.a1);
 28         return xd(a.a2,b.a2);
 29     }
 30 }bac[maxn];
 31 struct CIR
 32 {
 33     double r,x,y;
 34     inline void read() { scanf("%lf %lf %lf",&r,&x,&y); }
 35     inline NODE mid() { return (NODE) {x,y}; }
 36     inline double calc(NODE p) { return atan2(p.y-y,p.x-x); }
 37     inline double C() { return 2*pi*r; }
 38 }cir[maxn];
 39 struct LINE
 40 {
 41     double a,b,c;
 42     inline double dis(NODE p) { return fabs(a*p.x+b*p.y+c)/sqrt(qua(a)+qua(b)); }
 43     inline double key(NODE p) { return p.x*a+p.y*b+c; }
 44 };
 45 
 46 inline double dis(NODE a,NODE b) { return sqrt(qua(a.x-b.x) + qua(a.y-b.y)); }
 47 
 48 inline bool have(CIR c1,CIR c2) { return dis(c1.mid(),c2.mid())<c1.r+c2.r; }
 49 
 50 inline bool cat(CIR c1,CIR c2) { return xd(dis(c1.mid(),c2.mid()),fabs(c1.r-c2.r)); }
 51 
 52 inline LINE cross(CIR c1,CIR c2) { return (LINE) {2*(c2.x-c1.x),2*(c2.y-c1.y),(qua(c2.r)-qua(c2.x)-qua(c2.y))-(qua(c1.r)-qua(c1.x)-qua(c1.y))}; }
 53 
 54 inline void work()
 55 {
 56     int tot,i,j; double rest,p,q,a,b,now; LINE l;
 57     for (i = n;i;--i)
 58     {
 59         tot = 0; rest = 0; now = 0;
 60         for (j = i+1;j <= n;++j)
 61         {
 62             if (cat(cir[i],cir[j]))
 63             {
 64                 if (cir[i].r > cir[j].r) continue;
 65                 else break;
 66             }
 67             if (have(cir[i],cir[j]))
 68             {
 69                 p = cir[i].calc(cir[j].mid()) + pi;
 70                 l = cross(cir[i],cir[j]);
 71                 q = l.dis(cir[i].mid());
 72                 q = acos(q/cir[i].r);
 73                 if (cir[i].r < cir[j].r&&l.key(cir[i].mid())*l.key(cir[j].mid()) > 0)
 74                     q = pi - q;
 75                 a = p - q; b = p + q;
 76                 if (dd(a,0) && xd(b,2*pi))
 77                     bac[++tot] = (angle) {a,b};
 78                 else if (a < 0)
 79                 {
 80                     bac[++tot] = (angle) {a+2*pi,2*pi};
 81                     bac[++tot] = (angle) {0,b};
 82                 }
 83                 else
 84                 {
 85                     bac[++tot] = (angle) {a,2*pi};
 86                     bac[++tot] = (angle) {0,b-2*pi};
 87                 }
 88             }
 89         }
 90         if (j != n+1) continue;
 91         sort(bac+1,bac+tot+1);
 92         for (int j = 1;j <= tot;++j)
 93         {
 94             if (bac[j].a1 > now)
 95             {
 96                 rest += bac[j].a1 - now;
 97                 now = bac[j].a2;
 98             }
 99             else now = max(now,bac[j].a2);
100         }
101         rest += 2*pi - now;
102         ans += rest/(2*pi) * cir[i].C();
103     }
104 }
105 
106 int main()
107 {
108     freopen("1043.in","r",stdin);
109     freopen("1043.out","w",stdout);
110     scanf("%d",&n);
111     for (int i = 1;i <= n;++i) cir[i].read();
112     work();
113     printf("%.3lf",ans);
114     fclose(stdin); fclose(stdout);
115     return 0;
116 }

View Code