You are given an array a with n distinct integers. Construct an array b by permuting a such that for every non-empty subset of indices S = {x1, x2, ..., xk} (1 ≤ xi ≤ n, 0 < k < n) the sums of elements on that positions in a and b are different, i. e.
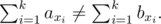
The first line contains one integer n (1 ≤ n ≤ 22) — the size of the array.
The second line contains n space-separated distinct integers a1, a2, ..., an (0 ≤ ai ≤ 109) — the elements of the array.
If there is no such array b, print -1.
Otherwise in the only line print n space-separated integers b1, b2, ..., bn. Note that b must be a permutation of a.
If there are multiple answers, print any of them.
2
1 2
2 1
4
1000 100 10 1
100 1 1000 10
An array x is a permutation of y, if we can shuffle elements of y such that it will coincide with x.
Note that the empty subset and the subset containing all indices are not counted.
讲一下题意把吧 这个题的意思就是n个数a1,a2,a3.......,这n个数重新排列构成b数组
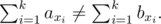
这个题吧 sum1(左边式子)和sum2(右边式子)都是从0开始加的,只要我能够使a[i]<b[i],那么sum2一定比sum1要大 这就是确定的
但是很明显,我做不到这个,
于是我这么构造,每个a都找到一个刚刚大于它的数,最大的数用最小的数代替,假设我现在计算的集合中没有最大的数和最小的数的组合
那么我的每个b元素都大于与之对应的a sum2一定大于sum1,
这时候我们再考虑最大的数和最小的数的组合在集合中的情况
由于我们的k<n && k>=1 那么我一定不可能把所有的情况都取干净 所以必定有一些集合是a < b没有取到的
这时候 正难则反 总共加和都是一样的,减去相差的,这时候sum1 > sum2了就
于是这样构造是能够满足题意的
丑陋的代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int arr[30];
int res[30];
int bin(int left,int right,int n)
{
int mid ;
while(left < right)
{
mid = (left+right) >> 1;
if(res[mid] > n) {
right = mid;
}
else if(res[mid] == n) {
return res[mid+1];
}
else if(res[mid] < n) {
left = mid + 1;
}
}
return res[mid+1];
}
int main()
{
int n,i,j;
int maxn = 0;
bool color_flag = false;
scanf("%d",&n);
for(i =0 ; i < n; ++i) {
scanf("%d",arr+i);
res[i] = arr[i];
maxn = max(maxn,arr[i]);
}
sort(res,res+n);
for(i = 0; i < n - 1; ++i) {
if(arr[i] == maxn)
printf("%d ",res[0]);
else
printf("%d ",bin(0, n-1, arr[i]));
}
if(arr[i] == maxn)
printf("%d ",res[0]);
else
printf("%d ",bin(0, n-1, arr[i]));
}