计算机里的加减乘除四则运算,最基本的就是加法运算,其余三种运算都可以通过加法运算来实现。
I. 半加器 (Half Adder)
考虑一位二进制加法运算,如果不考虑进位的话,我们可以得到如下真值表:

A,B表示输入,C(Carry)表示进位,S(Sum)表示结果。
可以得到:
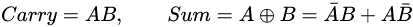
用逻辑门来实现:
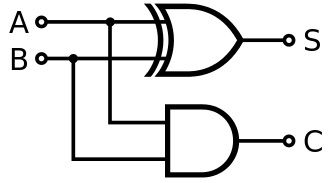
II. 全加器 (Full Adder)
有了半加器以后我们发现,这种加法器并不能实现多位数的加法,因此诞生了有进位的全加器。和半加器不一样,一个全加器有三个输入(A,B和低位进位)和两个输出(和以及进位输出)。
列出真值表:
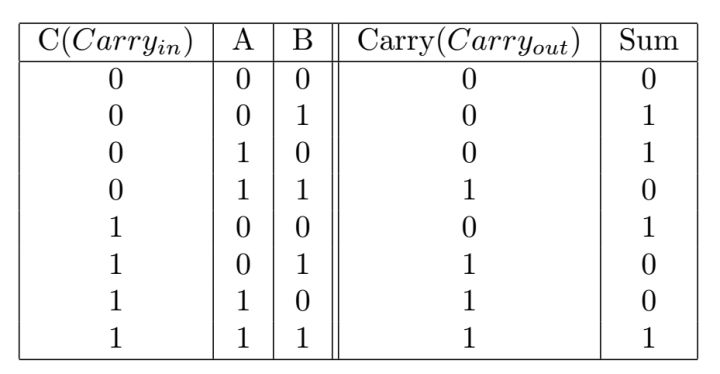
可以得到:


逻辑门实现:

III. 纹波进位加法器 (Ripple Carry Adder)
将n个全加器级联起来,就是一个n位的加法器,这就是逐级进位加法器。
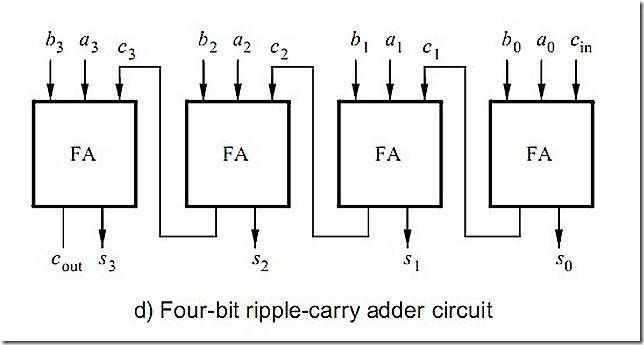
考虑到门电路中的电场状态改变需要时间,如果输入电平发生了变化,那么输出电平需要一段时间后才会响应,当然这段时间很小,小到了纳秒级别。因此,这种加法器有个缺点:每一位的进位输入依赖于上一位的进位输出,只有前一位的进位信号稳定后,这一位的全加器的运算才是有意义的。如果位数n很大的话,整个加法器会变慢,最后会限制CPU主频的提高。
IV. 超前进位加法器 (Carry-lookahead Adder)
既然级联一位的加法器算有这样的缺点,那就干脆直接设计一个位数足够大的加法器!
我们列出2位的全加器的真值表:

我们看到,随着n增大,真值表的行数是指数级别增长的。即使位数仅仅只有2,真值表的行数都达到了32,人工求解布尔表达式变得很困难。但是理论上,这样的全加器的确存在,而且实际上,有一个更优雅的设计方法。
再次考虑上面讲到的全加器,不再以级联的方式获得进位输入,而是直接根据输入,设计电路得到合适的进位,这样设计出来的加法器叫做超前进位加法器。
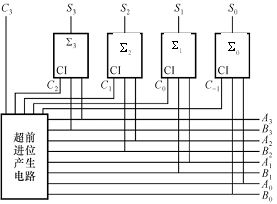
其中,每一级的进位可以由当前的两个位产生(generate),;或者由上一级传递(propagate)的进位
和当前输入累加导致的,
,因此下一级的进位是
。
因此,得到关于2位超前进位加法器的布尔表达式:

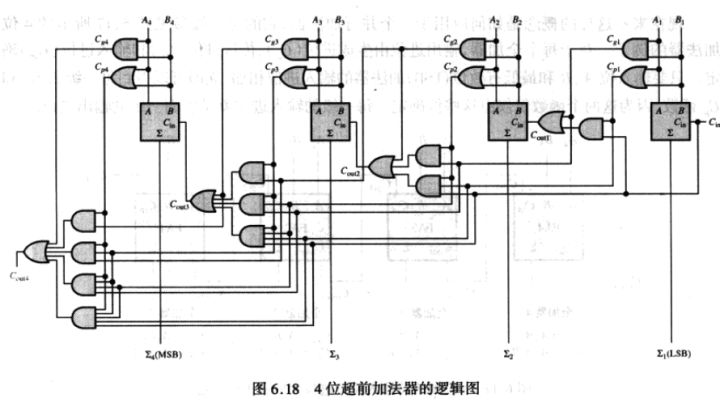
考虑到集成电路的面积,成本,功耗,散热等因素,超前进位加法器的位数一般不会过大。一般将几个超前进位加法器(如8位,16位)级联起来,得到位数够宽的加法器。
链接:https://www.zhihu.com/question/29707696/answer/114610705
来源:知乎