嘛嘛嘛,好像大家在实现Kruskal算法是都是用的边集数组,判断图的连通性咱不会,o(╯□╰)o(并查集诶)。
Kruskal算法:
规则:
(1)对每一条边按照从小到大进行排序。
(2)加入边的时候判断这条边与之前的边是否构成回路,如果构成则放弃这条边,否则就加入到最小生成树中。
边集数组:
struct Edge{
int begin;
int end;
int weight;
};
起点,终点,权值,这些都好懂的。
然后判断是否构成回路则是采用了并查集的思想:大家如果不懂并查集,可以看看这篇博客:并查集详解这篇博文,当初就是看这篇博文入门的。
整个代码:
#include <algorithm>
#include <iostream>
using namespace std;
const int MAXSIZE=100;
struct node{
int begin;
int end;
int weight;
}Gnode[MAXSIZE];
int parent[MAXSIZE];
int Parent(int f){
while(parent[f]!=f){
f=parent[f];
}
return f;
}
int cmp(node s1,node s2){
return s1.weight<s2.weight;
}
void Kruskal(node p[],int k){
int n,m;
for(int i=1;i<=MAXSIZE;i++){
parent[i]=i;
}
sort(p,p+k,cmp);
for(int i=1;i<=k;i++){
n=Parent(p[i].begin);
m=Parent(p[i].end);
if(n!=m){
cout<<'V'<<p[i].begin<<" "<<'V'<<p[i].end<<" "<<p[i].weight<<endl;
parent[n]=m;
}
}
}
int main(){
cout<<"Kruskal算法求最小生成树"<<endl;
cout<<"请输入图的边数"<<endl;
int num;
cin>>num;
for(int i=1;i<=num;i++){
cin>>Gnode[i].begin>>Gnode[i].end>>Gnode[i].weight;
}
cout<<"最小生成树的每条边级其权值"<<endl;
Kruskal(Gnode,num);
return 0;
}
附上测试数据:
10
1 2 6
1 3 1
1 4 5
2 3 5
2 5 3
3 4 5
3 5 6
3 6 4
4 6 2
5 6 6
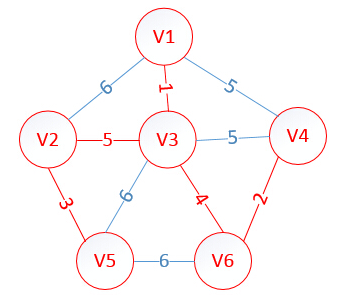
这是最后构建出的最小生成树。
并查集的思想很简单:首先判断两个点的父亲节点是否相同,不相同则让其中一个父亲节点成为另一个父亲节点的子节点,这样大家都在一个集合里了,如果最后加入的边首位节点都在一个集合里,显然这就构成回路了。
以上图为例: 1 3 parent[1]=1 parent[3]=3 则parent[1]=3 parent[3]=3
4 6 parent[4]=4 parent[6]=6 则parent[4]=6 parent[6]=6
2 5 parent[2]=2 parent[5]=5 则parent[2]=5 parent[5]=5
3 6 parent[3]=3 parent[6]=6 则parent[3]=6 parent[6]=6
2 3 parent[2]=5 parent[3]=6 则parent[5]=6 parent[3]=6
2 1 parent[2]=6 parent[1]=6 这样构成了回路
还有一点要强调的是上面代码中parent函数没有路径压缩这一过程,数据量比较大时,可能会超时,当然大家采用递归写法的话就不用考虑这个问题了。
int Parent(int f){
if(parent[f]!=f)
parent[f]=Parent(parent[f]);
return parent[f];
}