树链剖分,是一种可以把一棵有根树划分成许多条链,从而简单地实现树上修改与查询操作的 算法/数据结构(我也不知道属于哪个QwQ)。
当然这里的树链剖分是指重链剖分。
先放模板:P3384 【模板】轻重链剖分
(嘤嘤嘤她蓝了)
学习重链剖分,你首先要知道以下名词:
重儿子: 对于一个非叶子节点u,有许多子节点。而其中有一个子节点v,以他为根的子树的大小比其他子节点都大,那么v就是u的重儿子。
轻儿子: 不是重儿子就是轻儿子。
重链: 一条除了顶部是轻儿子,其他都是重儿子的路径。
光是文字好像不容易搞懂,那么来看看这张图:
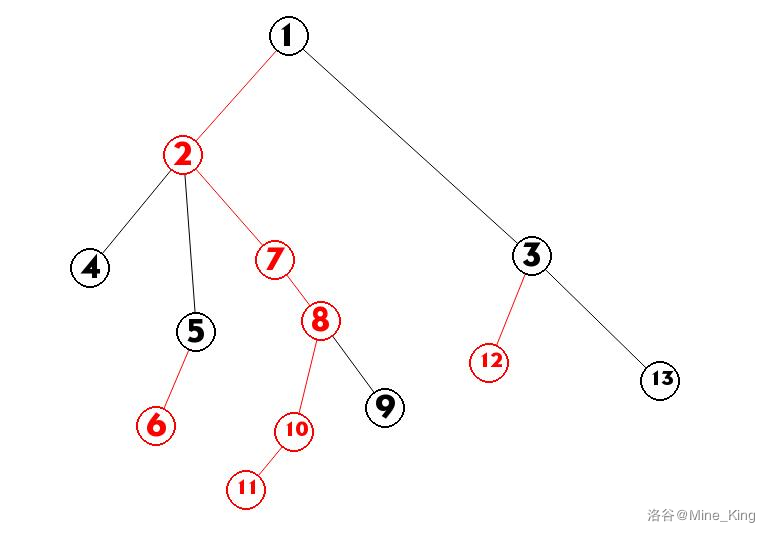
重儿子和重链已经用红色标出来了。
接下来就是树剖的实现啦!
树剖实际上就是两遍预处理。第一遍我们要求出每个点的父节点、深度、子树大小、重儿子,分别记为fa,depth,size,son。
其他三个都是信手拈来,而这个重儿子嘛……就是求子树最大的那个点啦!于是代码就很自然得写出来了:
void dfs1(int now,int F)
{
int k=0;//k用来记录当前找到的子树最大的点的子树大小
fa[now]=F,size[now]=1;
depth[now]=depth[F]+1;
//大家都熟悉的求父节点和深度
for(int i=g.hd[now];i;i=g.nxt[i])
if(g.to[i]!=F)//首先不能是父节点
{
dfs1(g.to[i],now);//递归
size[now]+=size[g.to[i]];//依然很熟悉的求子树大小
if(size[g.to[i]]>k)//这棵子树的大小比之前的更大呢
{
k=size[g.to[i]];
son[now]=g.to[i];
//那么就更新
}
}
return ;
}
第二遍我们要求每个点所在的重链的顶端和第几个被遍历,分别计为top和id。
那么这个怎么求呢?很简单,我们不用记录父节点了(上面已经求出来了),而是记录 这个点所在的重链的顶端 。这样就可以解决top了:
void dfs2(int now,int F)//这里的F是now所在的重链的顶端
{
top[now]=F;//记录top
id[now]=++cnt;//记录id
wt[id[now]]=a[now];//这里等下再解释
if(son[now]==0) return ;//重儿子是0,就是没有重儿子,那么就是叶子节点,结束。
dfs2(son[now],F);//要先递归重儿子哦
for(int i=g.hd[now];i;i=g.nxt[i])
if(g.to[i]!=fa[now]&&g.to[i]!=son[now])//是轻儿子
dfs2(g.to[i],g.to[i]);//递归
return ;
}
然后你就学会树剖了(逃
然后你就要解决修改和查询了。
在这之前,先观察一下id,可以发现在一条重链上,id是连续的。在一棵子树里也是。
然后我们就需要这个性质来解决修改和查询了。
先看第一个操作:
将树从x到y结点最短路径上所有节点的值都加上z
回想一下倍增LCA怎么搞?深度大的往上跳,直到父亲相同。这里也是一样。由于一条重链上id连续,所以每条重链求和只要让id[top[u]]到id[u]都加上k就OK了。而这个操作可以让线段树来完成。这也是为什么我之前在第二遍(dfs)的时候要wt[id[now]]=a[now];。线段树建树的时候就是把wt的值赋上去的。
之后,再让u跳到fa[top[u]]即可:
void add_path(int x,int y,int k)
{
while(top[x]!=top[y])//不在同一条重链上
{
if(depth[top[x]]<depth[top[y]]) swap(x,y);//让x是深度大的那个
tr.change(id[top[x]],id[x],1,k);//区间修改
x=fa[top[x]];//往上跳
}
if(depth[x]>depth[y]) swap(x,y);//这里在同一条重链上,要让x做深度小的那个了
tr.change(id[x],id[y],1,k);//修改他们中间的那段
return ;
}
操作2也一样,只不过把修改改成了查询:
int query_path(int x,int y)
{
int res=0;
while(top[x]!=top[y])
{
if(depth[top[x]]<depth[top[y]]) swap(x,y);
res=(res+tr.ask(id[top[x]],id[x],1))%Mod;//记得取模
x=fa[top[x]];
}
if(depth[x]>depth[y]) swap(x,y);
res=(res+tr.ask(id[x],id[y],1))%Mod;//这里也是
return res;
}
然后是操作3:。
将以x为根节点的子树内所有节点值都加上z。
由于子树内的id连续,所以最小的那个是id[u],共有size[u]个,所以修改的区间就是id[u]到id[u]+size[u]-1:
void add_son(int x,int k)
{
tr.change(id[x],id[x]+size[x]-1,1,k);
return ;
}
操作4也一样:
int query_son(int x)
{
return tr.ask(id[x],id[x]+size[x]-1,1);
}
好了,这题就结束了!总复杂度(O(nlog^2n))。
整体代码长这个亚子:
#include<cstdio>
#define MAXN 100005
#define int long long
using namespace std;
int n,m,Root,Mod,cnt;
int a[MAXN],wt[MAXN];
int fa[MAXN],size[MAXN],depth[MAXN];
int son[MAXN],top[MAXN],id[MAXN];
void swap(int &x,int &y)
{
int t=x;
x=y;
y=t;
return ;
}
struct graph
{
int tot,hd[MAXN];
int nxt[MAXN*2],to[MAXN*2];
void add(int u,int v)
{
tot++;
nxt[tot]=hd[u];
hd[u]=tot;
to[tot]=v;
return ;
}
}g;
struct Tree
{
int w[MAXN*4],l[MAXN*4],r[MAXN*4];
int f[MAXN*4];
void build(int ll,int rr,int k)
{
l[k]=ll,r[k]=rr;
if(ll==rr)
{
w[k]=wt[ll]%Mod;
return ;
}
int mid=(ll+rr)/2;
build(ll,mid,k*2);
build(mid+1,rr,k*2+1);
w[k]=(w[k*2]+w[k*2+1])%Mod;
return ;
}
void down(int k)
{
f[k*2]=(f[k*2]+f[k])%Mod;
f[k*2+1]=(f[k*2+1]+f[k])%Mod;
w[k*2]=(w[k*2]+f[k]*(r[k*2]-l[k*2]+1)%Mod)%Mod;
w[k*2+1]=(w[k*2+1]+f[k]*(r[k*2+1]-l[k*2+1]+1)%Mod)%Mod;
f[k]=0;
return ;
}
void change(int ll,int rr,int k,int x)
{
if(l[k]>=ll&&r[k]<=rr)
{
w[k]=(w[k]+x*(r[k]-l[k]+1)%Mod)%Mod;
f[k]=(f[k]+x)%Mod;
return ;
}
if(f[k]) down(k);
int mid=(l[k]+r[k])/2;
if(ll<=mid) change(ll,rr,k*2,x);
if(rr>mid) change(ll,rr,k*2+1,x);
w[k]=w[k*2]+w[k*2+1];
return ;
}
int ask(int ll,int rr,int k)
{
if(l[k]>=ll&&r[k]<=rr) return w[k]%Mod;
if(f[k]) down(k);
int res=0,mid=(l[k]+r[k])/2;
if(ll<=mid) res=(res+ask(ll,rr,k*2))%Mod;
if(rr>mid) res=(res+ask(ll,rr,k*2+1))%Mod;
return res;
}
}tr;
void dfs1(int now,int F)
{
int k=0;
fa[now]=F,size[now]=1;
depth[now]=depth[F]+1;
for(int i=g.hd[now];i;i=g.nxt[i])
if(g.to[i]!=F)
{
dfs1(g.to[i],now);
size[now]+=size[g.to[i]];
if(size[g.to[i]]>k)
{
k=size[g.to[i]];
son[now]=g.to[i];
}
}
return ;
}
void dfs2(int now,int F)
{
top[now]=F;
id[now]=++cnt;
wt[id[now]]=a[now];
if(son[now]==0) return ;
dfs2(son[now],F);
for(int i=g.hd[now];i;i=g.nxt[i])
if(g.to[i]!=fa[now]&&g.to[i]!=son[now])
dfs2(g.to[i],g.to[i]);
return ;
}
void add_path(int x,int y,int k)
{
while(top[x]!=top[y])
{
if(depth[top[x]]<depth[top[y]]) swap(x,y);
tr.change(id[top[x]],id[x],1,k);
x=fa[top[x]];
}
if(depth[x]>depth[y]) swap(x,y);
tr.change(id[x],id[y],1,k);
return ;
}
int query_path(int x,int y)
{
int res=0;
while(top[x]!=top[y])
{
if(depth[top[x]]<depth[top[y]]) swap(x,y);
res=(res+tr.ask(id[top[x]],id[x],1))%Mod;
x=fa[top[x]];
}
if(depth[x]>depth[y]) swap(x,y);
res=(res+tr.ask(id[x],id[y],1))%Mod;
return res;
}
void add_son(int x,int k)
{
tr.change(id[x],id[x]+size[x]-1,1,k);
return ;
}
int query_son(int x)
{
return tr.ask(id[x],id[x]+size[x]-1,1);
}
signed main()
{
scanf("%lld%lld%lld%lld",&n,&m,&Root,&Mod);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
for(int i=1;i<n;i++)
{
int u,v;
scanf("%lld%lld",&u,&v);
g.add(u,v);
g.add(v,u);
}
dfs1(Root,0);
dfs2(Root,Root);
tr.build(1,n,1);
for(int i=1;i<=m;i++)
{
int opt;
scanf("%lld",&opt);
if(opt==1)
{
int x,y,k;
scanf("%lld%lld%lld",&x,&y,&k);
add_path(x,y,k);
}
else if(opt==2)
{
int x,y;
scanf("%lld%lld",&x,&y);
printf("%lld
",query_path(x,y));
}
else if(opt==3)
{
int x,k;
scanf("%lld%lld",&x,&k);
add_son(x,k);
}
else
{
int x;
scanf("%lld",&x);
printf("%lld
",query_son(x));
}
}
return 0;
}
当然,树剖也能用来求(LCA),怎么求的话……看看上面的操作1操作2就能明白吧。