这场是第一场没有米的BC...
大概也是想震一震那些一听说没米了就不打BC的人吧
这次的题目质量比以往高了许多
(然而我并没有打这一场BC
但是今天下午到现在做的过程中真的学到了不少知识呢
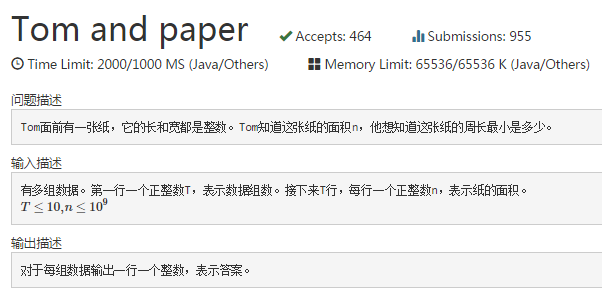
A题略水...
1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<cmath> 5 int T,n; 6 int main(){ 7 scanf("%d",&T); 8 while (T--){ 9 scanf("%d",&n); 10 int tmp; 11 for (int i=1;i<=sqrt(n);i++) if (n%i==0) tmp=i; 12 printf("%d ",2*(n/tmp+tmp)); 13 } 14 return 0; 15 }
然而第二题就不是非常简单的呢...
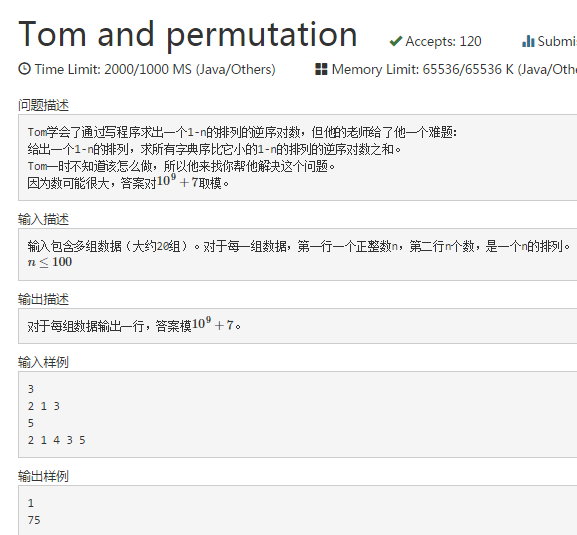
开始啊..我打算数位DP搞搞,然而突然发现排列是不能有重复数字的啊...
想到一个容易入手的状态 也就解决了这道题
我们需要让这些排列都小于读进来的排列
然后思考一下这些排列都有什么共性呢?
显然一定是由一段与排列相同的数字组成的前缀构成的,而接下来的一位一定小于排列,剩下的就随意了
这么一来好像问题就迎刃而解了
枚举与原串相同的位数(0~n-1),以及接下来一位的数字(小于原串该位置上的数字且在前面的位置中没出现过)
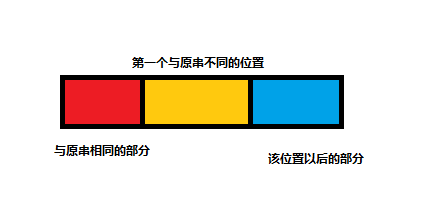
设当前枚举的黄色部分的位置为i,那么显然这样的字符串有(n-i)!种(即后面蓝色部分的n-i个数字的全排列)
这些字符串对答案的贡献分几部分考虑
1)红色部分内部的逆序对*(n-i)!,原串所有的前缀的逆序对数量可以通过树状数组预处理出
2)红色部分与黄色+蓝色部分的逆序对数,
可以用树状数组维护黄色+蓝色部分的值(即每向后走一格就将前一个数从树状数组中删去)
然后枚举红色部分的每一个元素,统计逆序对数,最后乘上(n-i)!
3)黄色部分与蓝色部分的逆序对数,直接与红色部分一样的答案最后-1即可(即把自己与自己减掉),
当然get的时候传参改成数值-1也是可以的
4)蓝色部分的逆序对数,这个在(n-i)!个字符串中都是不一样的,于是我们可以考虑总数
对于一个n个数的排列,我们考虑其中的两个数,它们成为逆序对的次数为C(n,2)*(n-2)!
所以逆序对总数为C(n,2)^2*(n-2)!
然后这道题就做完了,但是却对拍了一个下午都没找出哪里写错...
最后写两点做题过程中积累的东西吧...
1)C++的数组和Pas毕竟不一样...赋值啊什么的不能顶到maxn..而且居然本地不会出现RE
2)while not eof do 在C++里是以很奇怪的方式替代的呢...
1 #include<cstdio> 2 #include<cstdlib> 3 #include<iostream> 4 #include<cmath> 5 #include<cstring> 6 #define tt 1000000007 7 #define maxn 110 8 #define ll long long 9 using namespace std; 10 int n,a[maxn],tr[maxn]; 11 ll w[maxn],p[maxn],b[maxn]; 12 bool used[maxn]; 13 int get(int x){ 14 int tmp=0; 15 while (x) tmp+=tr[x],x-=x&(-x); 16 return tmp; 17 } 18 void put(int x,int y){ 19 while (x<=n) tr[x]+=y,x+=x&(-x); 20 } 21 void build(){ 22 w[0]=1;for(int i=1;i<maxn;i++) w[i]=(w[i-1]*i)%tt; 23 p[1]=0;for (int i=2;i<maxn;i++) { 24 ll tmp=i*(i-1)/2; 25 p[i]=((tmp*tmp%tt)*w[i-2])%tt; 26 } 27 } 28 void solve(){ 29 ll ans=0; 30 memset(tr,0,sizeof(tr)); 31 for (int i=1;i<=n;i++) b[i]=(b[i-1]+get(n-a[i]+1))%tt,put(n-a[i]+1,1); 32 memset(tr,0,sizeof(tr)); 33 memset(used,true,sizeof(used)); 34 for (int i=1;i<=n;i++) put(i,1); 35 for (int i=1;i<=n;i++){ 36 if (i!=1) put(a[i-1],-1),used[a[i-1]]=false; 37 for (int j=1;j<a[i];j++) if (used[j]){ 38 ll tmp=b[i-1];for (int k=1;k<i;k++) tmp=(tmp+get(a[k]))%tt; 39 if (j!=1) tmp=(tmp+get(j-1))%tt; 40 tmp=((tmp*w[n-i])+p[n-i])%tt; 41 ans=(ans+tmp)%tt; 42 } 43 } 44 cout<<ans<<endl; 45 } 46 int main(){ 47 build(); 48 while (cin>>n){ 49 for (int i=1;i<=n;i++) scanf("%d",a+i); 50 solve(); 51 } 52 return 0; 53 }
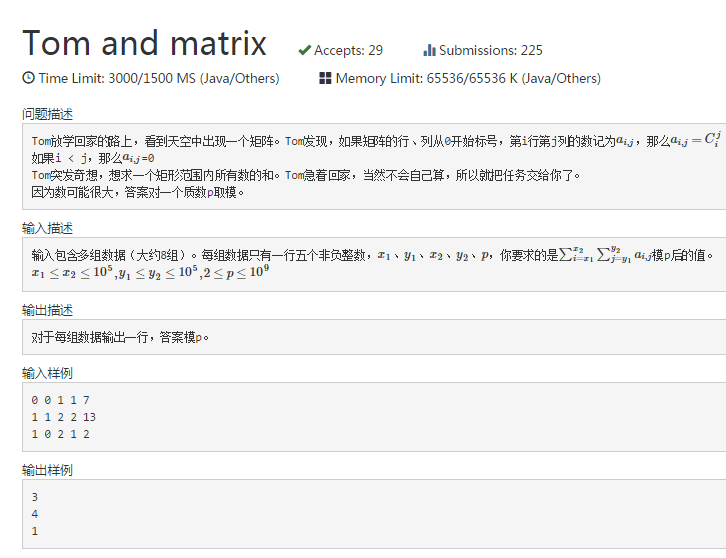
浓浓的数学味...于是又得去补充几个知识了呢
首先带取模的组合数是不能直接求解的...因为一旦C(n,m)中假设n>模数p,n!中就会出现p这个因子
然后C(n,m)就不可避地计算出了0...
这个时候要用到Lucas定理,递归定义
1 ll lucas(int n,int m){ 2 if (m==0) return 1; 3 if (n<tt&&m<tt) return c(n,m); 4 return lucas(n/tt,m/tt)*lucas(n%tt,m%tt)%tt; 5 }
另一个就是连续的组合数快速求解...
刚开始我一直在寻找同一行之间的关系..因为毕竟之前如果是整行是可以直接算的
然而实际上列存在着一定的关系
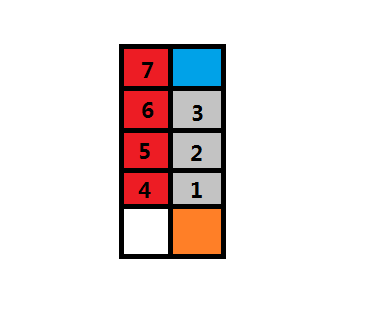
我们考虑这样一列上连续一段的求解(如图中红色部分)
根据杨辉三角的构造方法,C(n,m)=C(n-1,m)+C(n-1,m-1)
我们设4号格子的位置为(i,a)
最顶端红色格子的位置为(i,b)
C(a+1,i+1)=C(a,i)+C(a,i+1) → C(a,i)=C(a+1,i+1)-C(a,i+1)
显然...sigma(C(i,j))(a<=j<=b)=C(a+1,i+1)-C(b,i+1)
在图中也就是橙色格子-蓝色格子
然后对于每一列求解就可以了,但是要注意可能a,b不是真正的a,b
因为我们现在考虑的是建立在红色部分都至少为1的基础上的,于是对于每一列都要对行标号进行处理
另外还要注意,即使实际代表意义上不可能但取模意义下的减法可能会减出负的,也要处理
1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #define maxn 100010 5 #define ll long long 6 int x1,y1,x2,y2,tt; 7 ll fac[maxn],inv[maxn]; 8 int max(int a,int b){ 9 if (a>b) return a; 10 return b; 11 } 12 ll mul(ll a,ll b){ 13 ll ans=1,w=a; 14 while (b){ 15 if (b%2==1) ans=ans*w%tt; 16 w=w*w%tt;b=b>>1; 17 } 18 return ans; 19 } 20 void build(){ 21 fac[0]=1;for (int i=1;i<maxn;i++) fac[i]=fac[i-1]*i%tt; 22 inv[0]=1;for (int i=1;i<maxn;i++) inv[i]=mul(fac[i],tt-2); 23 } 24 ll c(int n,int m){ 25 return fac[n]*inv[m]%tt*inv[n-m]%tt; 26 } 27 ll lucas(int n,int m){ 28 if (m==0) return 1; 29 if (n<tt&&m<tt) return c(n,m); 30 return lucas(n/tt,m/tt)*lucas(n%tt,m%tt)%tt; 31 } 32 ll query(int n,int m){ 33 if (n<m) return 0; 34 return lucas(n,m); 35 } 36 void solve(){ 37 ll ans=0; 38 for (int i=y1;i<=y2;i++) { 39 if (x2<i) continue; 40 int l=max(x1,i),r=x2; 41 if (l==i){l++;ans=(ans+1)%tt;} 42 ans=(ans+query(r+1,i+1)-query(l,i+1)+tt)%tt; 43 } 44 printf("%lld ",ans); 45 } 46 int main(){ 47 while (scanf("%d",&x1)!=EOF){ 48 scanf("%d%d%d%d",&y1,&x2,&y2,&tt); 49 build(); 50 solve(); 51 } 52 return 0; 53 }