滑雪场坐落在FJ省西北部的若干座山上。从空中鸟瞰,滑雪场可以看作一个有向无环图,每条弧代表一个斜坡(即雪道),弧的方向代表斜坡下降的方向。你的团队负责每周定时清理雪道。你们拥有一架直升飞机,每次飞行可以从总部带一个人降落到滑雪场的某个地点,然后再飞回总部。从降落的地点出发,这个人可以顺着斜坡向下滑行,并清理他所经过的雪道。由于每次飞行的耗费是固定的,为了最小化耗费,你想知道如何用最少的飞行次数才能完成清理雪道的任务。
题意就是给定一张DAG,求每条边起码经过一次求覆盖所有边的最小路径条数 如图
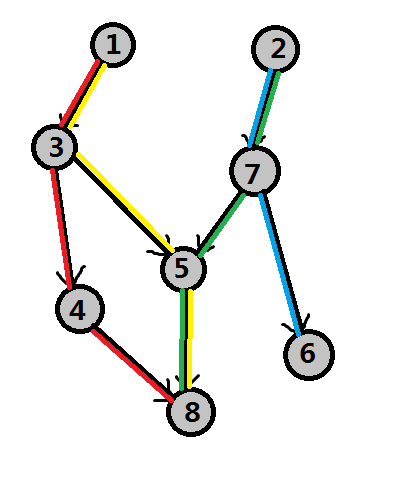
这时的答案为4
很容易看出,就是在每条边都经过一次的情况下求一次最小流
即带有下界的最小流
解决方法很简单:
对于一条(x,y)
从x到y连一条容量为1,费用为-INF的边,根据最小费用最大流的性质
我们可以看出显然这条边是会流到的
然后鉴于每条边经过的次数不止一次,所以从x到y再连一条容量为INF,费用为0的边
源点向所有入度为0的点连边,所有出度为0的边向汇点连边
但是显然求最大流是求不完的,什么时候停止呢?
每次增广必定增广出的是费用最小的一条路径
当图中还有边未经过的时候,增光出来的路径中毕竟有费用为-INF的边
当图中所有的边都经过的时候,增广出的路径费用为0
这个时候就可以停止了
另外事后考虑了一个问题:
这样做为什么能保证是最小流呢?
每次增广然后标记感觉只是模拟
但是会发现,每条未经过的边权值为-INF,和最小费用最大流结合
保证每次选出的路径能尽量多填满一些边
反向弧的存在又使结果的正确性有了更多重的保证
program xjt7; const maxn = 110;maxm = 100010;INF = 10000000007; var n,m,e,s,t,x,y:int64; i,j:longint; fa,next,link,w,cost,rec,son:array[-1..maxm]of int64; dis,opt,pos,pre,b,lea:array[-1..maxn]of int64; vis:array[-1..maxn]of boolean; function min(a,b:int64):int64; begin if a<b then exit(a) else exit(b); end; procedure add(x,y,z,cst:int64); begin inc(e);fa[e]:=y;next[e]:=link[x];link[x]:=e;w[e]:=z;cost[e]:=cst;rec[e]:=e+1;son[e]:=x; inc(e);fa[e]:=x;next[e]:=link[y];link[y]:=e;w[e]:=0;cost[e]:=-cst;rec[e]:=e-1;son[e]:=y; end; function spfa:boolean; var head,tail,x,j:int64; begin fillchar(vis,sizeof(vis),true); fillchar(dis,sizeof(dis),63); head:=0;tail:=1;opt[1]:=s;dis[s]:=0;vis[s]:=false; while head<>tail do begin head:=(head+1) mod maxn; x:=opt[head];j:=link[x]; while j<>0 do begin if (w[j]>0)and(dis[x]+cost[j]<dis[fa[j]]) then begin dis[fa[j]]:=dis[x]+cost[j];pre[fa[j]]:=j; if vis[fa[j]] then begin vis[fa[j]]:=false; tail:=(tail+1) mod maxn; opt[tail]:=fa[j]; end; end; j:=next[j]; end; vis[x]:=true; end; if dis[t]<>dis[t+1] then exit(true); exit(false); end; procedure MCMF; var sum,u,mn,ans:int64; begin ans:=0; while spfa do begin sum:=0; u:=t;mn:=INF; while u<>s do begin mn:=min(mn,w[pre[u]]); u:=son[pre[u]]; end; u:=t; while u<>s do begin inc(sum,mn*cost[pre[u]]); dec(w[pre[u]],mn);inc(w[rec[pre[u]]],mn); u:=son[pre[u]]; end; if sum>0 then break; inc(ans,mn); end; writeln(ans); end; begin //assign(input,'xjt7.in');reset(input); readln(n); fillchar(b,sizeof(b),0); for i:=1 to n do begin read(lea[i]); for j:=1 to lea[i] do begin read(y);add(i,y,1,-INF);add(i,y,INF,0); inc(b[y]); end; readln; end; s:=0;t:=n+1; for i:=1 to n do if b[i]=0 then add(s,i,INF,1); for i:=1 to n do if lea[i]=0 then add(i,t,INF,1); MCMF; end.