FHQ treap 的整理
treap = tree + heap,即同时满足二叉搜索树和堆的性质。
为了使树尽可能的保证两边的大小平衡,所以有一个key值,使他满足堆得性质,来维护树的平衡,key值是随机的。
treap有一般平衡树的功能,前驱、后继、第k大、查询排名、插入、删除。也比较好写
但是对于区间上的问题是不能做的,例如
- 区间增减
- 区间求最值
- 区间反转(倒序)
- 区间移动(把一段剪切、粘贴)
(splay是可以做的)
但是有一种神奇的数据结构,即可以满足treap的功能,也可以区间上进行操作——FHQ treap
FHQ treap 只有两个基本操作,所以代码量也小的多。
split
分离,讲一个treap分成两个treap。
有两种分离的类型,一个是按照权值val分,小于等于k的分成一个,大于的一个。另一种是取出区间上的前k个数。
权值:
对于一颗treap,小于等于k的点是存在于一颗子树中的,但是这颗子树可能有大于k的,所以在拆分时,是要重建这棵树的。
1 void Split(int now,int k,int &x,int &y) { 2 if (!now) x = y = 0; 3 else { 4 if (val[now] <= k) 5 x = now,Split(ch[now][1],k,ch[now][1],y); 6 else 7 y = now,Split(ch[now][0],k,x,ch[now][0]); 8 pushup(now); 9 } 10 }
代码非常奇妙,它引用了两个值,x,y,这两个值就是重建的最重要的两个变量,一定要有取地址符。
x引用的是一个小于等于k的节点(假设是a)的右儿子,y引用的是一个大于k的节点左儿子。
这里a是小于等于k的,它的左子树也是小于等于k的,但是右儿子却不一定是小于k的,所以这里取出它的右儿子,当遇到第一个小于k的节点是,让它成为a的右儿子。
如下图,k=6,那么a是小于6的,往右走,发现右儿子是大于6的,所以a的右儿子是要改变的,接下来往左走的过程中,将a的右儿子指向权值为6的点即可。
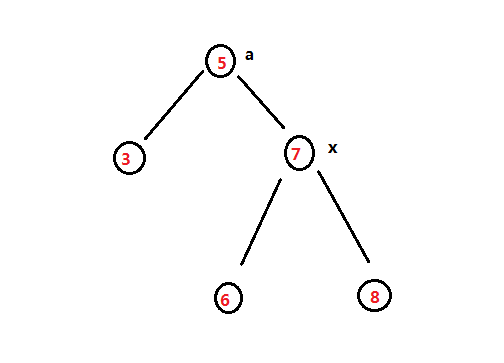
重建的过程:如果当前点now的值小于k那么,他的左边一定都是小于k的,所以往右走。
复杂度 $O(logn)$
区间上前k个数
1 void Split(int now,int k,int &x,int &y) { 2 if (!now) x=y=0; 3 else { 4 if (k <= siz[ch[now][0]]) 5 y = now,Split(ch[now][0],k,x,ch[now][0]); 6 else 7 x = now,Split(ch[now][1],k-siz[ch[now][0]]-1,ch[now][1],y); 8 pushup(now); 9 } 10 }
原理是一样的,不详细说了。
复杂度,$O(logn)$
merge
合并两颗子树,保证第一颗树的所有点的权值都小于第二颗子树的所有节点。
那么重建只要满足堆的性质就好了。
还是有两个变量x,y,
1 int Merge(int x,int y) { 2 if (!x || !y) return x + y; 3 if (key[x] < key[y]) { 4 ch[x][1] = Merge(ch[x][1],y); 5 pushup(x); return x; 6 } 7 else { 8 ch[y][0] = Merge(x,ch[y][0]); 9 pushup(y); return y; 10 } 11 }
这里会发现,当x树的key小时,只将x的左半边加入到重建的树中,y子树小时,只将它的右半边加入到子树中。为了满足treap的性质。
复杂度 $O(logn)$
两个基本操作就完成了。
insert
插入一个权值为k的数。
过程:把treap分成两个,小于等于k的,大于k的,把x和两个子树合并即可
Split(Root,k,x,y);
Root = Merge(Merge(x,makenode(k)),y);
delete
删除一个权值为k的数。
过程:先分成小于等于k的 a 和大于k的 b ,之后将x分成小于等于k-1的 c 和大于k-1的 d ,d就是k,所以将d的两个儿子合并起来,然后与c,b合并即可;
Split(Root,k,x,y); Split(x,k-1,x,z); z = Merge(ch[z][0],ch[z][1]); Root = Merge(Merge(x,z),y);
k的排名
求k的排名
过程:分成小于等于k-1的 x ,和大于k-1 的 y 两个子树,子树x的大小就是k的排名。
Split(Root,k-1,x,y); printf("%d ",siz[x]+1); Root = Merge(x,y);
第k个数
求第k个数
过程:和splay,treap一样的求法;
inline int getkth(int p,int k) { while (true) { if (k == siz[ch[p][0]] + 1) return p; if (ch[p][0] && k <= siz[ch[p][0]]) p = ch[p][0]; else k-= ((ch[p][0] ? siz[ch[p][0]] : 0) + 1),p = ch[p][1]; } }
前驱
求k的排名
过程:分成小于等于k-1的 x ,和大于k-1 的 y 两个子树,子树x中最大的数就是x的前驱。
Split(Root,k-1,x,y); printf("%d ",val[getkth(x,siz[x])]); Root = Merge(x,y);
后继
求k的排名
过程:分成小于等于k的 x ,和大于k 的 y 两个子树,子树y中最小的数就是x的前驱。
Split(Root,k,x,y); printf("%d ",val[getkth(y,1)]); Root = Merge(x,y);
FHQtreap的基本操作就是这些了
例题
普通平衡树

1 #include<cstdio> 2 #include<algorithm> 3 4 using namespace std; 5 6 const int N = 500100; 7 int ch[N][2],siz[N],key[N],val[N]; 8 int tn,Root; 9 10 inline char nc() { 11 static char buf[100000],*p1 = buf,*p2 = buf; 12 return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2) ? EOF : *p1++; 13 } 14 inline int read() { 15 int x = 0,f = 1;char ch = getchar(); 16 for (; ch<'0'||ch>'9'; ch = getchar()) 17 if (ch=='-') f = -1; 18 for (; ch>='0'&&ch<='9'; ch = getchar()) 19 x = x*10+ch-'0'; 20 return x * f; 21 } 22 inline void pushup(int x) { 23 siz[x] = siz[ch[x][0]] + siz[ch[x][1]] + 1; 24 } 25 inline int makenode(int x) { 26 ++tn;val[tn] = x;siz[tn] = 1;key[tn] = rand();return tn; 27 } 28 29 int Merge(int x,int y) { 30 if (!x || !y) return x + y; 31 if (key[x] < key[y]) { 32 ch[x][1] = Merge(ch[x][1],y); 33 pushup(x); return x; 34 } 35 else { 36 ch[y][0] = Merge(x,ch[y][0]); 37 pushup(y); return y; 38 } 39 } 40 void Split(int now,int k,int &x,int &y) { 41 if (!now) x = y = 0; 42 else { 43 if (val[now] <= k) 44 x = now,Split(ch[now][1],k,ch[now][1],y); 45 else 46 y = now,Split(ch[now][0],k,x,ch[now][0]); 47 pushup(now); 48 } 49 } 50 inline int getkth(int p,int k) { 51 while (true) { 52 if (k == siz[ch[p][0]] + 1) return p; 53 if (ch[p][0] && k <= siz[ch[p][0]]) p = ch[p][0]; 54 else k-= ((ch[p][0] ? siz[ch[p][0]] : 0) + 1),p = ch[p][1]; 55 } 56 } 57 int main() { 58 int x,y,z,opt,k,n = read(); 59 while (n--) { 60 opt = read(),k = read(); 61 if (opt==1) { 62 Split(Root,k,x,y); 63 Root = Merge(Merge(x,makenode(k)),y); 64 } 65 else if (opt==2) { 66 Split(Root,k,x,y); 67 Split(x,k-1,x,z); 68 z = Merge(ch[z][0],ch[z][1]); 69 Root = Merge(Merge(x,z),y); 70 } 71 else if (opt==3) { 72 Split(Root,k-1,x,y); 73 printf("%d ",siz[x]+1); 74 Root = Merge(x,y); 75 } 76 else if (opt==4) 77 printf("%d ",val[getkth(Root,k)]); 78 else if (opt==5) { 79 Split(Root,k-1,x,y); 80 printf("%d ",val[getkth(x,siz[x])]); 81 Root = Merge(x,y); 82 } 83 else { 84 Split(Root,k,x,y); 85 printf("%d ",val[getkth(y,1)]); 86 Root = Merge(x,y); 87 } 88 } 89 return 0; 90 }
文艺平衡树

1 #include<cstdio> 2 #include<algorithm> 3 4 using namespace std; 5 6 const int N = 500100; 7 8 int ch[N][2],tag[N],val[N],siz[N],key[N]; 9 int tn,Root,n,m; 10 11 inline char nc() { 12 static char buf[100000],*p1 = buf,*p2 = buf; 13 return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2) ? EOF : *p1++; 14 } 15 inline int read() { 16 int x = 0,f = 1;char ch = nc(); 17 for (; ch<'0'||ch>'9'; ch = nc()) 18 if (ch=='-') f = -1; 19 for (; ch>='0'&&ch<='9'; ch = nc()) 20 x = x*10+ch-'0'; 21 return x * f; 22 } 23 inline void pushup(int x) { 24 siz[x] = siz[ch[x][0]] + siz[ch[x][1]] + 1; 25 } 26 inline void pushdown(int x) { 27 if (x && tag[x]) { 28 tag[x] ^= 1; 29 swap(ch[x][0],ch[x][1]); 30 if (ch[x][0]) tag[ch[x][0]] ^= 1; 31 if (ch[x][1]) tag[ch[x][1]] ^= 1; 32 } 33 } 34 inline int makenode(int x) { 35 ++tn;siz[tn] = 1;val[tn] = x;key[tn] = rand();return tn; 36 } 37 int merge(int x,int y) { 38 if (!x || !y) return x + y; 39 pushdown(x);pushdown(y); 40 if (key[x] < key[y]) { 41 ch[x][1] = merge(ch[x][1],y); 42 pushup(x);return x; 43 } 44 else { 45 ch[y][0] = merge(x,ch[y][0]); 46 pushup(y);return y; 47 } 48 } 49 void split(int now,int k,int &x,int &y) { 50 if (!now) x = y = 0; 51 else { 52 pushdown(now); 53 if (k<=siz[ch[now][0]]) 54 y = now,split(ch[now][0],k,x,ch[now][0]); 55 else 56 x = now,split(ch[now][1],k-siz[ch[now][0]]-1,ch[now][1],y); 57 pushup(now); 58 } 59 } 60 inline void rever(int l,int r) { 61 int a,b,c,d; 62 split(Root,r,a,b); 63 split(a,l-1,c,d); 64 tag[d] ^= 1; 65 Root = merge(merge(c,d),b); 66 } 67 void print(int x) { 68 if (!x) return ; 69 pushdown(x); 70 print(ch[x][0]); 71 printf("%d ",val[x]); 72 print(ch[x][1]); 73 } 74 int main() { 75 n = read(),m = read(); 76 for (int i=1; i<=n; ++i) { 77 Root = merge(Root,makenode(i)); 78 } 79 while (m--) { 80 int a = read(),b = read(); 81 rever(a,b); 82 } 83 print(Root); 84 return 0; 85 }
=========
