1568: [JSOI2008]Blue Mary开公司（超哥线段树）

1568: [JSOI2008]Blue Mary开公司

Time Limit: 15 Sec  Memory Limit: 162 MB
Submit: 1198  Solved: 418

Description

Input

第一行 ：一个整数N ，表示方案和询问的总数。 

接下来N行，每行开头一个单词“Query”或“Project”。 

若单词为Query，则后接一个整数T，表示Blue Mary询问第T天的最大收益。 

若单词为Project，则后接两个实数S，P，表示该种设计方案第一天的收益S，以及以后每天比上一天多出的收益P。

1 <= N <= 100000 1 <= T <=50000 0 < P < 100，| S | <= 10^6 

提示：本题读写数据量可能相当巨大，请选手注意选择高效的文件读写方式。

Output

对于每一个Query，输出一个整数，表示询问的答案，并精确到整百元（以百元为单位，

例如：该天最大收益为210或290时，均应该输出2）。没有方案时回答询问要输出0

Sample Input

10
Project 5.10200 0.65000
Project 2.76200 1.43000
Query 4
Query 2
Project 3.80200 1.17000
Query 2
Query 3
Query 1
Project 4.58200 0.91000
Project 5.36200 0.39000

Sample Output

0
0
0
0
0

HINT

 

Source

分析

超哥线段树，记录每个点的最大的线段是谁。查询时用这条线段查询。

那么怎么记录呢，（当时这个问题困惑我好久），线段树只能记录一段区间，对于一条线段它只记录一段区间，怎么保存区间所有的线段？

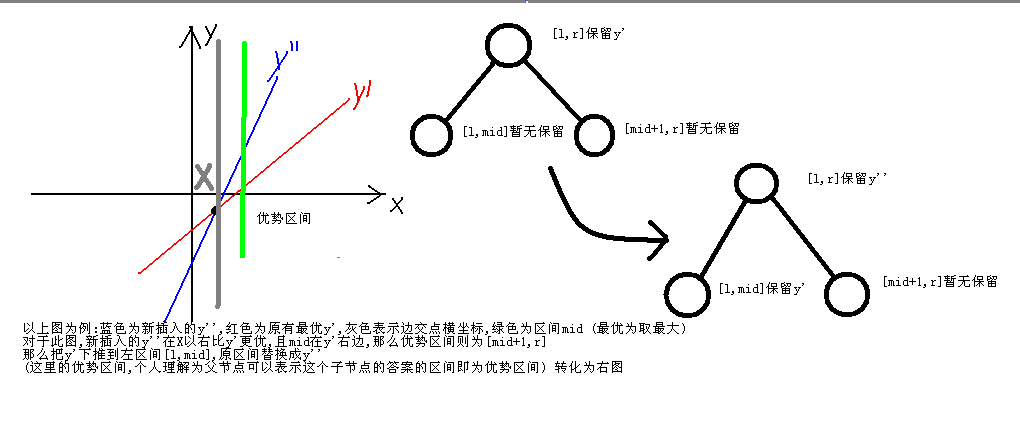
借用一张图说明这一点。

对于原来的区间[l,r]表示y'这条线段，就是让[l,r]区间的所有的线段是y'，然后来了一条线段y”，显然在x点右边，y”要比y’更优，但是线段树只能从中间劈开，不能[l,x][x,r]这样，所以我们就找到中点mid = (l+r)/2，这样[mid,r]这段区间可以直接更新了，左区间继续像这样分，全部都更新完就好了。

code

#include<cstdio>
#include<algorithm>
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
 
using namespace std;
 
const int MAXN = 500010;
int fut[MAXN<<2];
double a[MAXN<<2],b[MAXN<<2];
char opt[15];
int tot;
 
int pd(int x,int y,int p)
{
    return a[x]+(p-1)*b[x] > a[y]+(p-1)*b[y];  
}
void update(int l,int r,int rt,int x)
{
    if (l==r)
    {
        if (pd(x,fut[rt],l)) fut[rt] = x;
        return ;
    }
    int m = (l+r)>>1;
    if (b[x]>b[fut[rt]])
    {
        if (pd(x,fut[rt],m)) update(lson,fut[rt]), fut[rt] = x;
        else update(rson,x);
    }
    if (b[x]<b[fut[rt]])
    {
        if (pd(x,fut[rt],m)) update(rson,fut[rt]), fut[rt] = x;
        else update(lson,x);
    }
}
double getans(int k,int x)
{
    return a[k]+(x-1)*b[k];
}
double query(int l,int r,int rt,int x)
{
    if (l==r) return getans(fut[rt],x);
    int m = (l+r)>>1;
    double ans = getans(fut[rt],x);
    if (x<=m) ans = max(ans,query(lson,x));
    else ans = max(ans,query(rson,x));
    return ans;
}
int main()
{
    int n,x;
    scanf("%d",&n);
    for (int i=1; i<=n; ++i)
    {
        scanf("%s",opt);
        if (opt[0]=='P')
        {
            ++tot;
            scanf("%lf%lf",&a[tot],&b[tot]);
            update(1,n,1,tot);
        }
        else
        {
            scanf("%d",&x);
            double t1 = query(1,n,1,x);
            int t2 = t1;
            printf("%d
",t2/100);
        }
    }   
    return 0;
}