Tempter of the Bone

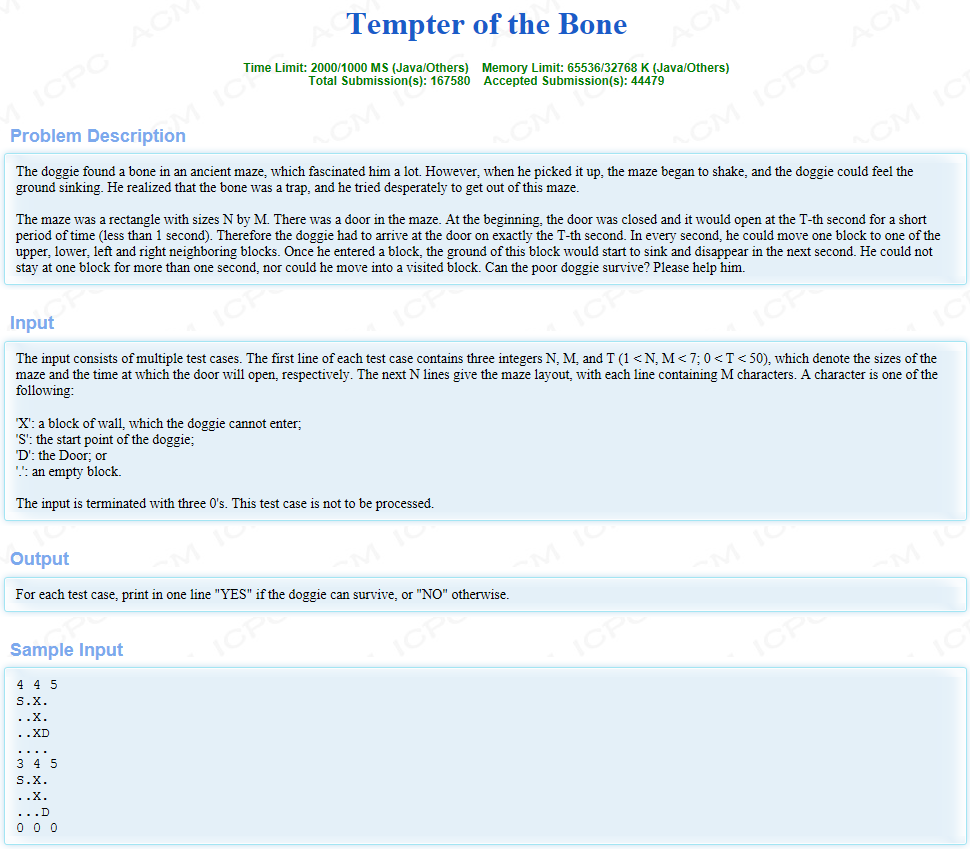
 本题要求在指定时间点到达目的地, 一开始用的广搜, 但是搜出的是最短路径, 理解错题意了... 使用深搜, 只要搜索到一个能在指定时间点到达目的地的路径就返回(由于深搜可能会爆栈, 所以要用到奇偶剪枝)

奇偶剪枝结论:若 t-[abs(ex-sx)+abs(ey-sy)] 结果为非偶数（奇数），则无法在t步恰好到达(奇偶剪枝详细说明请参考百度百科)

#include <iostream>
#include <cstring>
#include <cmath>
using namespace std;

int n, m, t, sx, sy, ex, ey, flag;
char map[10][10];
int vis[10][10];
int dir[4][2] = {{1,0},{0,1},{-1,0},{0,-1}};

void dfs(int x, int y, int ti)
{
	int dx, dy;
	if(flag == 1 || ti > t)	return ; 
	// 在规定时间内正好到达终点
	if(map[x][y] == 'D' && ti == t)
	{
		flag = 1;	// 找到了这么一条路 
		return ;	// 返回 
	}
	
	int tem = t - ti - abs(ex-x) - abs(ey-y);//剪枝的核心代码
	if(tem < 0 || tem & 1)//剪枝：如果剩余的步数已经不足以走到出口，且必须是偶数，偶数-偶数=偶数，奇数-奇数=偶数，
        return;
	// 四个方向遍历 
	for(int i = 0; i < 4; ++ i)
	{
		dx = x + dir[i][0];
		dy = y + dir[i][1];
		
		// 如果 越界 或 走到墙X 或 已访问过 
		if(dx < 0 || dx >= n || dy < 0 || dy >= m || map[dx][dy] == 'X' || vis[dx][dy])
			continue;
			
		// 新扩展的点标记走过, 对该点进行DFS 
		vis[dx][dy] = 1;
		dfs(dx, dy, ti + 1);
		// 回溯后将标记撤回 
		vis[dx][dy] = 0;
	}
	return ;
}

int main()
{
	while(cin >> n >> m >> t)
	{
		if(n == 0 && m == 0 && t == 0)	break;
		memset(vis, 0, sizeof(vis));
		
		for(int i = 0; i < n; ++ i)
		{
			cin >> map[i];
		}
		
		int wall = 0;
		flag = 0;
		for(int i = 0; i < n; i ++)
        {
            for(int j = 0; j < m; j ++)
            {
                if(map[i][j] == 'S')
                {
                    sx = i;
					sy = j;
                }
                if(map[i][j]=='D')
                {
                    ex = i;
					ey = j;
                }
                if(map[i][j]=='X')	wall ++;
            }
        }

		if(t > n * m - wall - 1)
		{
			cout << "NO" << endl;
			continue;
		}
		
		vis[sx][sy] = 1;
		dfs(sx, sy, 0);
	
		if(flag)	cout << "YES" << endl;
		else	cout << "NO" << endl;
	}
	
	return 0;
}

/*
4 4 5
S.X.
..X.
..XD
....
3 4 5
S.X.
..X.
...D
0 0 0
*/