Catalan数

Catalan数

Catalan数是继斐波拉契数列之后OI最喜欢考的数列。

简单讲一下Catalan的相关用途

• 出栈入栈
• 括号序列匹配
• 凸多边形的三角形分割

而Catalan的求法也很多:

1. (Cat_n=dfrac{dbinom{2n}{n}}{n+1})
2. (Cat_n=dbinom{2n}{n}-dbinom{2n}{n-1})
3. 递推式 (Cat_n=Cat_{n-1} imes dfrac{4n-2}{n+1})
4. 定义式 (Cat_n=Cat_0cdot Cat_{n-1}+Cat_1cdot Cat_{n_2}+cdots+Cat_{n-1}*Cat_0)

通常前两个就够了

关键

Catalan数难的不是它的计算，而是如何想到它。这里有个小技巧：

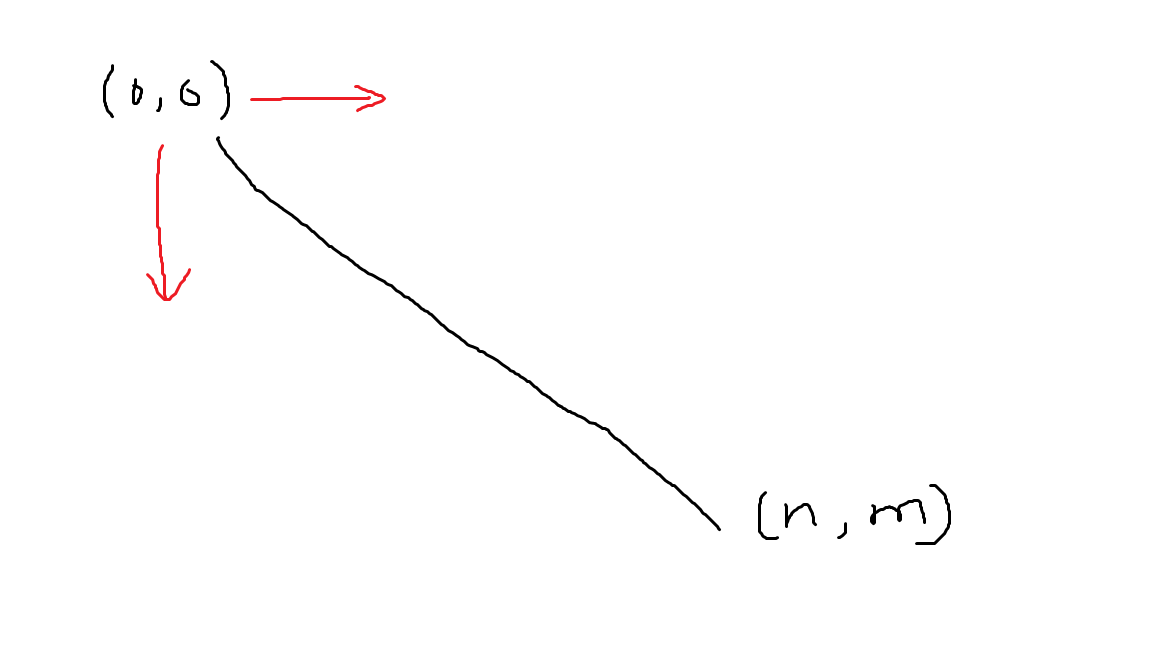
假设在黑线上方均为合法。横着的红线就可以看做

• 左括号
• 入栈

而竖着的红线就可以看成

• 右括号
• 出站

这样就将图形与实际问题有机的结合了起来。

相关问题

  - 饭后，姐姐洗碗，妹妹把姐姐洗过的碗一个一个放进碗橱摞成一摞。一共有n个不同的碗，洗前也是摞成一摞的，也许因为小妹贪玩而使碗拿进碗橱不及时，姐姐则把洗过的碗摞在旁边，问：小妹摞起的碗有多少种可能的方式？

  - 一个有*n*个1和*n*个-1组成的字串，且前k个数的和均不小于0，那这种字串的总数为多少？

  - P=A1A2A3……An，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？

2. n个节点的二叉树有多少种构型？

3. 有n+1个叶子的满二叉树的个数？

4、在n*n的格子中，只在下三角行走，每次横或竖走一格，有多少中走法？

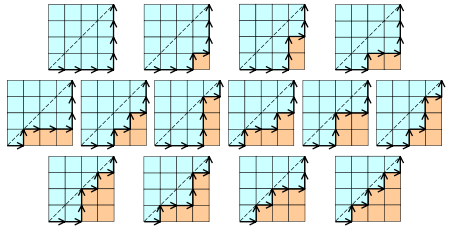
5、将一个凸n+2边形区域分成三角形区域的方法数？

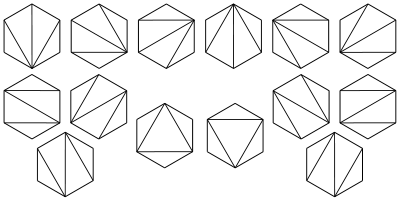
6、在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数？

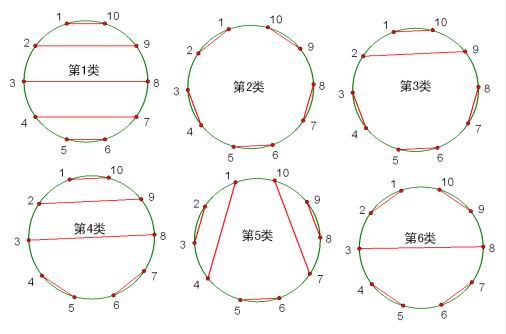
7、n个长方形填充一个高度为n的阶梯状图形的方法个数？