深度学习中的优化算法总结
以下内容简单的汇总了在深度学习中常见的优化算法,每个算法都集中回答:是什么?(原理思想)有什么用?(优缺点)怎么用?(在tensorflow中的使用)
目录
1.SGD
1.1Batch gradient descent
1.2Stochastic gradient descent
1.3Mini -batch grdient descent
1.4三种梯度下降算法的比较
2.Momentum
3.Nesterov
4.Agadgrad
5.Adadelta
6.RMSprop
7.Adam
8.Adamax
9.Nadam
10.经验之谈
10.1几种算法下降过程的可视化
10.2优化算法的选择
10.3优化算法总结
1.SGD
3种不同的梯度下降方法,区别在于每次参数更新时计算的样本数据量不同。
1.1 Batch gradient descent
1.1.1 是什么?
每进行1次参数更新,需要计算整个数据样本集:
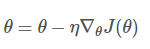
for i in range(nb_epochs): params_grad = evaluate_gradient(loss_function, data, params) params = params - learning_rate * params_grad
1.1.2 怎么用?
optimizer = tf.train.GradientDescentOptimizer(learning_rate=self.learning_rate) #这个类是实现梯度下降算法的优化器。(结合理论可以看到,这个构造函数需要的一个学习率就行了) __init__(learning_rate, use_locking=False,name=’GradientDescent’) 作用:创建一个梯度下降优化器对象 参数: learning_rate: A Tensor or a floating point value. 要使用的学习率 use_locking: 要是True的话,就对于更新操作(update operations.)使用锁 name: 名字,可选,默认是”GradientDescent”.
1.2 Stochastic gradient descent
1.2.1 是什么?
每进行1次参数更新,只需要计算1个数据样本:
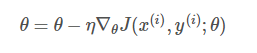
for i in range(nb_epochs):
np.random.shuffle(data)
for example in data:
params_grad = evaluate_gradient(loss_function, example, params)
params = params - learning_rate * params_grad
1.3 Mini -batch grdient descent
1.3.1是什么?
每进行1次参数更新,需要计算1个mini-batch数据样本:
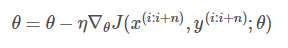
for i in range(nb_epochs): np.random.shuffle(data) for batch in get_batches(data, batch_size=50): params_grad = evaluate_gradient(loss_function, batch, params) params = params - learning_rate * params_grad
1.4 三种随机下降梯度的比较
Batch gradient descent的收敛速度太慢,而且会大量多余的计算(比如计算相似的样本)。
Stochastic gradient descent虽然大大加速了收敛速度,但是它的梯度下降的波动非常大(high variance)。
Mini-batch gradient descent中和了2者的优缺点,所以SGD算法通常也默认是Mini-batch gradient descent。
【Mini-batch gradient descent的缺点】
然而Mini-batch gradient descent也不能保证很好地收敛。主要有以下缺点:
-
选择一个合适的learning rate是非常困难的
学习率太低会收敛缓慢,学习率过高会使收敛时的波动过大。
-
所有参数都是用同样的learning rate
对于稀疏数据或特征,有时我们希望对于不经常出现的特征的参数更新快一些,对于常出现的特征更新慢一些。这个时候SGD就不能满足要求了。
-
sgd容易收敛到局部最优解,并且在某些情况可能被困在鞍点
在合适的初始化和step size的情况下,鞍点的影响没那么大。
正是因为SGD这些缺点,才有后续提出的各种算法。
2.Momentum
2.1 是什么?
momentum利用了物理学中动量的思想,通过积累之前的动量(mt−1mt−1)来加速当前的梯度。
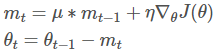
其中,μμ是动量因子,通常被设置为0.9或近似值。
2.2 有什么用?
- 参数下降初期,加上前一次参数更新值;如果前后2次下降方向一致,乘上较大的μμ能够很好的加速。
- 参数下降中后期,在局部最小值附近来回震荡时,gradient→0gradient→0,μμ使得更新幅度增大,跳出陷阱。
- 在梯度方向改变时,momentum能够降低参数更新速度,从而减少震荡;在梯度方向相同时,momentum可以加速参数更新, 从而加速收敛。
- 总而言之,momentum能够加速SGD收敛,抑制震荡。
2.3 怎么用?
optimizer = tf.train.MomentumOptimizer(lr, 0.9)
3.Nesterov
3.1 是什么?
NAG 法则首先(试探性地)在之前积累的梯度方向(棕色向量)前进一大步,再根据当前地情况修正,以得到最终的前进方向(绿色向量)。这种基于预测的更新方法,使我们避免过快地前进,并提高了算法地响应能力,大大改进了 RNN 在一些任务上的表现。


Momentum与Nexterov的对比,如下图:
-
Momentum:蓝色向量
Momentum首先计算当前的梯度值(短的蓝色向量),然后加上之前累计的梯度/动量(长的蓝色向量)。
-
Nexterov:绿色向量
Nexterov首先先计算之前累计的梯度/动量(长的棕色向量),然后加上当前梯度值进行矫正后(−μ∗mt−1−μ∗mt−1)的梯度值(红色向量),得到的就是最终Nexterov的更新值(绿色向量)。
Momentum和Nexterov都是为了使梯度更新更灵活。但是人工设计的学习率总是有些生硬,下面介绍几种自适应学习率的方法。
4.Agadgrad
4.1是什么?
Adagrad是对学习率进行了一个约束。

4.2有什么用?
【特点】
- 前期ntnt较小的时候,regularizer较大,能够放大梯度
- 后期ntnt较大的时候,regularizer较小,能够缩小梯度
- 中后期,分母上梯度平方的累加会越来越大,使gradient→0gradient→0,使得训练提前结束。
【缺点】
- 由公式可以看出,仍依赖于人工设置的一个全局学习率 ηη
- ηη 设置过大的话,会使regularizer过于敏感,对梯度调节太大。
- 最重要的是,中后期分母上的梯度平方累加会越来越大,使gradient→0gradient→0,使得训练提前结束,无法继续学习。
Adadelta主要就针对最后1个缺点做了改进。
4.3怎么用?
optimizer = tf.train.AdagradientOptimizer(learning_rate=self.learning_rate)
5.Adadelta
5.1是什么?
Adadelta依然对学习率进行了约束,但是在计算上进行了简化。
Adagrad会累加之前所有梯度的平方,而Adadelata只需累加固定大小的项,并且也不直接存储这些项,仅仅是计算对应的近似平均值。
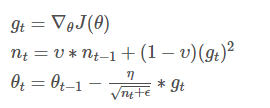
在此处Adadelta还是依赖全局学习率的,然后作者又利用近似牛顿迭代法,做了一些改进:
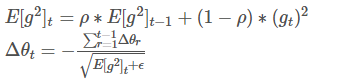
其中,E代表求期望。
此时可以看出Adadelta已经不依赖全局learning rate了。
5.2有什么用?
- 训练初中期,加速效果不错,很快。
- 训练后期,反复在局部最小值附近抖动。
6.RMSprop
6.1是什么?
RMSprop可以看做Adadelta的一个特例。

如果再求根的话,就变成RMS(Root Mean Squared,均方根):

此时,RMS就可以作为学习率 ηη的一个约束:
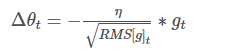
比较好的一套参数设置为:η=0.001,γ=0.9
6.2有什么用?
- 其实RMSprop依然依赖于全局学习率
- RMSprop的效果介于Adagrad和Adadelta之间
- 适合处理非平稳目标——对于RNN效果很好。
6.3怎么用?
optimizer = tf.train.RMSPropOptimizer(0.001, 0.9)
7.Adam
7.1是什么?
Adam(Adaptive Moment Estimation)本质上时带有动量项的RMSprop。

7.2有什么用?
- Adam梯度经过偏置校正后,每一次迭代学习率都有一个固定范围,使得参数比较平稳。
- 结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点
- 为不同的参数计算不同的自适应学习率
- 也适用于大多非凸优化问题——适用于大数据集和高维空间。
7.3怎么用?
optimizer = tf.train.AdamOptimizer(learning_rate=self.learning_rate, epsilon=1e-08) Adam 这个名字来源于 adaptive moment estimation,自适应矩估计。概率论中矩的含义是:如果一个随机变量 X 服从某个分布,X 的一阶矩是 E(X),也就是样本平均值,X 的二阶矩就是 E(X^2),也就是样本平方的平均值。Adam 算法根据损失函数对每个参数的梯度的一阶矩估计和二阶矩估计动态调整针对于每个参数的学习速率。Adam 也是基于梯度下降的方法,但是每次迭代参数的学习步长都有一个确定的范围,不会因为很大的梯度导致很大的学习步长,参数的值比较稳定。it does not require stationary objective, works with sparse gradients, naturally performs a form of step size annealing。 直接进行优化 train_op = optimizer.minimize(loss) 获得提取进行截断等处理 gradients, v = zip(*optimizer.compute_gradients(loss))#此函数用来将计算得到的梯度和方差进行拆分 compute_gradients(loss,var_list=None,gate_gradients=GATE_OP,aggregation_method=None,colocate_gradients_with_ops=False,grad_loss=None) 作用:对于在变量列表(var_list)中的变量计算对于损失函数的梯度,这个函数返回一个(梯度,变量)对的列表,其中梯度就是相对应变量的梯度了。这是minimize()函数的第一个部分, 参数: loss: 待减小的值 var_list: 默认是在GraphKey.TRAINABLE_VARIABLES. gate_gradients: How to gate the computation of gradients. Can be GATE_NONE, GATE_OP, or GATE_GRAPH. aggregation_method: Specifies the method used to combine gradient terms. Valid values are defined in the class AggregationMethod. colocate_gradients_with_ops: If True, try colocating gradients with the corresponding op. grad_loss: Optional. A Tensor holding the gradient computed for loss. gradients, _ = tf.clip_by_global_norm(gradients, self.max_gradient_norm)#梯度修剪,防止梯度爆炸 train_op = optimizer.apply_gradients(zip(gradients, v), global_step=self.global_step)#应用梯度来更新权值 apply_gradients(grads_and_vars,global_step=None,name=None) 作用:把梯度“应用”(Apply)到变量上面去。其实就是按照梯度下降的方式加到上面去。这是minimize()函数的第二个步骤。 返回一个应用的操作。 参数: grads_and_vars: compute_gradients()函数返回的(gradient, variable)对的列表 global_step: Optional Variable to increment by one after the variables have been updated. name: 可选,名字
8.Adamax
8.1是什么?
Adamax是Adam的一种变体,此方法对学习率的上限提供了一个更简单的范围。
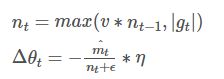
Adamax的学习率边界范围更简单
9.Nadam
9.1是什么?
Nadam类似于带有Nexterov动量项的Adam。
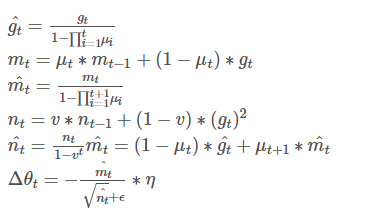
可以看出,Nadam对学习率有更强的约束,同时对梯度的更新也有更直接的影响。
一般而言,在使用带动量的RMSprop或Adam的问题上,使用Nadam可以取得更好的结果。
10.经验之谈
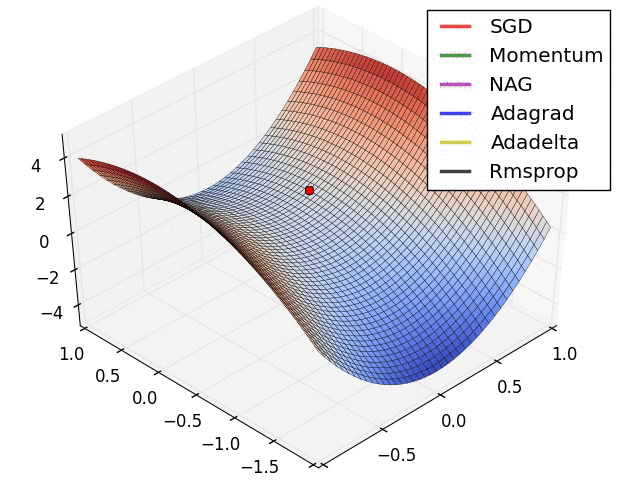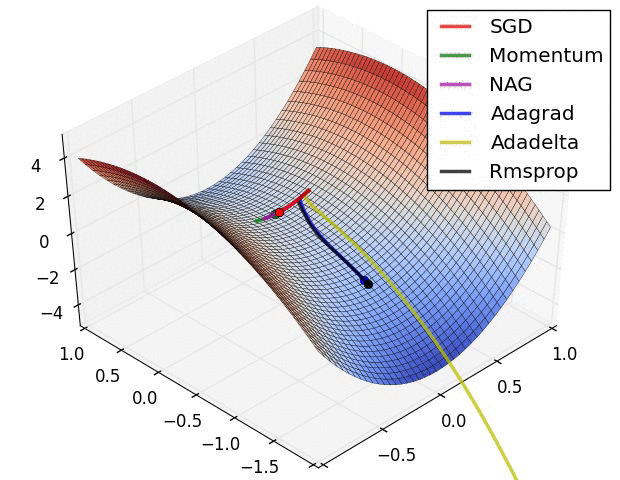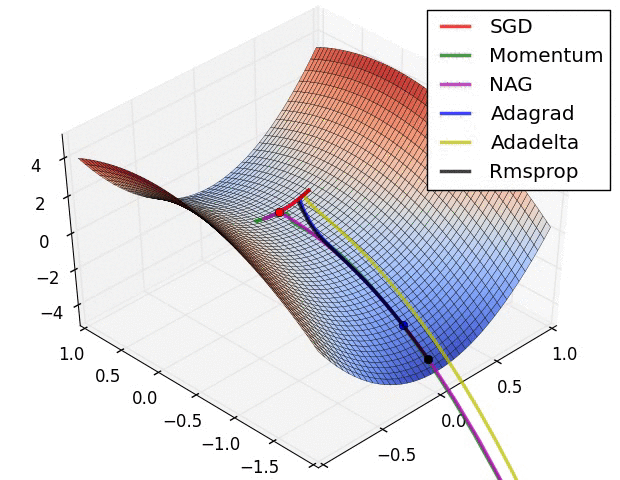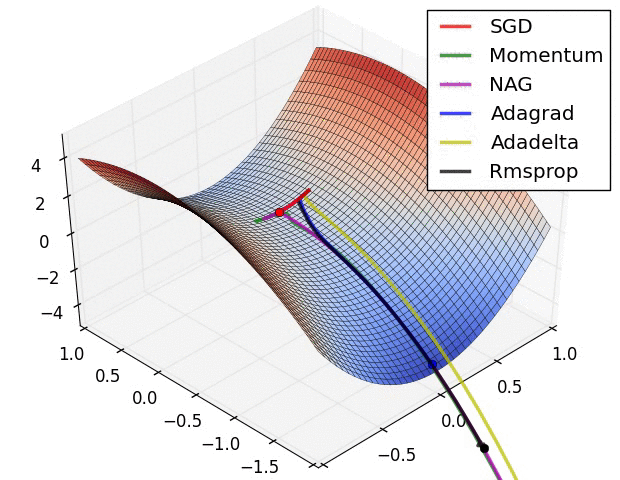
10.1几种算法下降过程的可视化
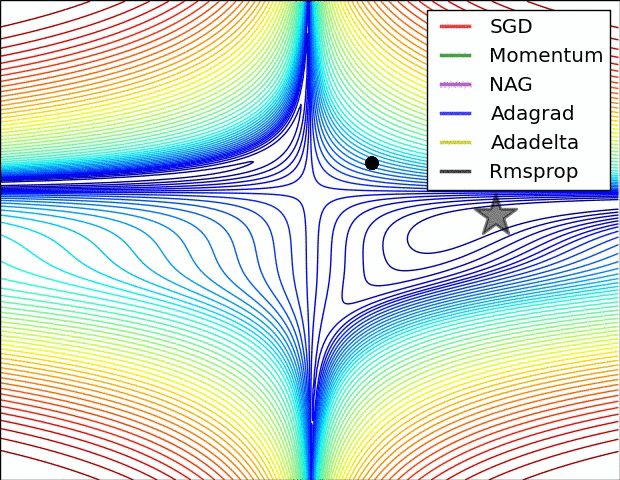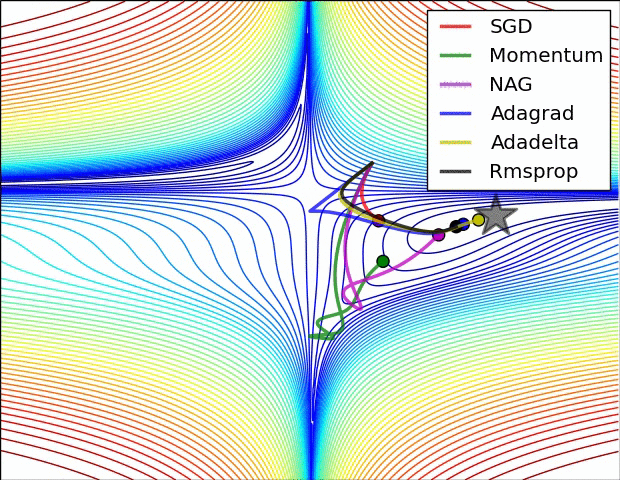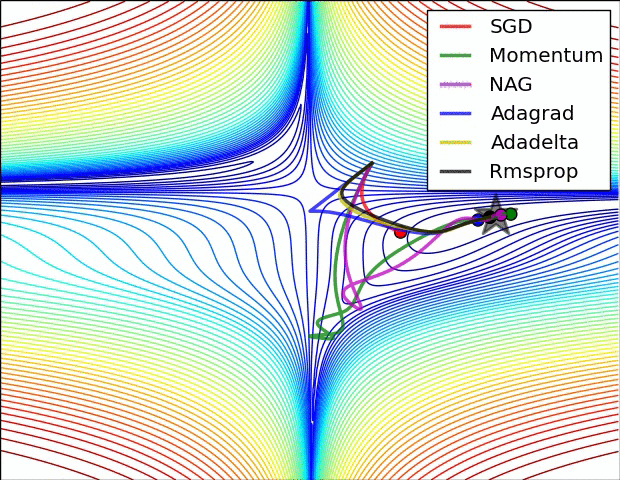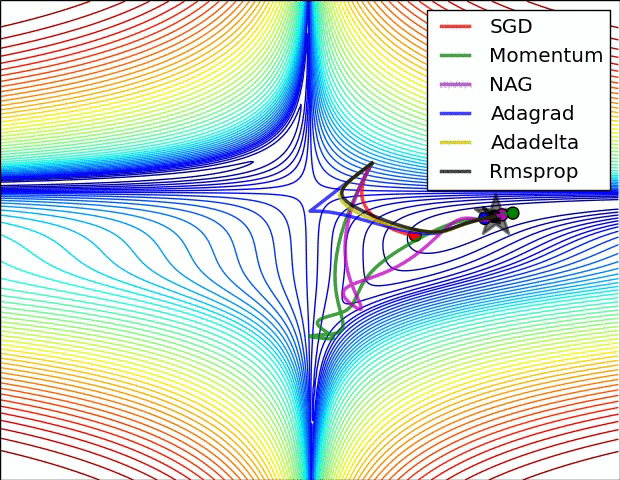
10.2优化算法的选择
- 对于稀疏数据,尽量使用学习率可自适应的算法,不用手动调节,而且最好采用默认参数
- SGD通常训练时间最长,但是在好的初始化和学习率调度方案下,结果往往更可靠。但SGD容易困在鞍点,这个缺点也不能忽略。
- 如果在意收敛的速度,并且需要训练比较深比较复杂的网络时,推荐使用学习率自适应的优化方法。
- Adagrad,Adadelta和RMSprop是比较相近的算法,表现都差不多。
- 在能使用带动量的RMSprop或者Adam的地方,使用Nadam往往能取得更好的效果。
【学习率自适应的优化算法】:
Adagrad, Adadelta, RMSprop, Adam, Adamax, Nadam
优化SGD的其他策略
Shuffling and Curriculum Learning
Shuffling就是打乱数据,每一次epoch之后 shuffle一次数据,可以避免训练样本的先后次序影响优化的结果。
但另一方面,在有些问题上,给训练数据一个有意义的顺序,可能会得到更好的性能和更好的收敛。这种给训练数据建立有意义的顺序的方法被叫做Curriculum Learning。
Batch Normalization
为了有效的学习参数,我们一般在一开始把参数初始化成0均值和单位方差。但是在训练过程中,参数会被更新到不同的数值范围,使得normalization的效果消失,从而导致训练速度变慢或梯度爆炸等等问题(当网络越来越深的时候)。
BN给每个batch的数据恢复了normalization,同时这些对数据的更改都是可还原的,即normalization了中间层的参数,又没有丢失中间层的表达能力。
使用BN之后,我们就可以使用更高的学习率,也不用再在参数初始化上花费那么多注意力。
BN还有正则化的作用,同时也削弱了对Dropout的需求。
Early Stopping
在训练的时候我们会监控validation的误差,并且会(要有耐心)提前停止训练,如果验证集的error没有很大的改进。
Gradient noise
在梯度更新的时候加一个高斯噪声:
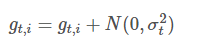
方差值的初始化策略是:

Neelakantan等人表明,噪声使得网络的鲁棒性更好,而且对于深度复杂的网络训练很有帮助。
他们猜想添加了噪声之后,会使得模型有更多机会逃离局部最优解(深度模型经常容易陷入局部最优解)
10.3优化算法总结
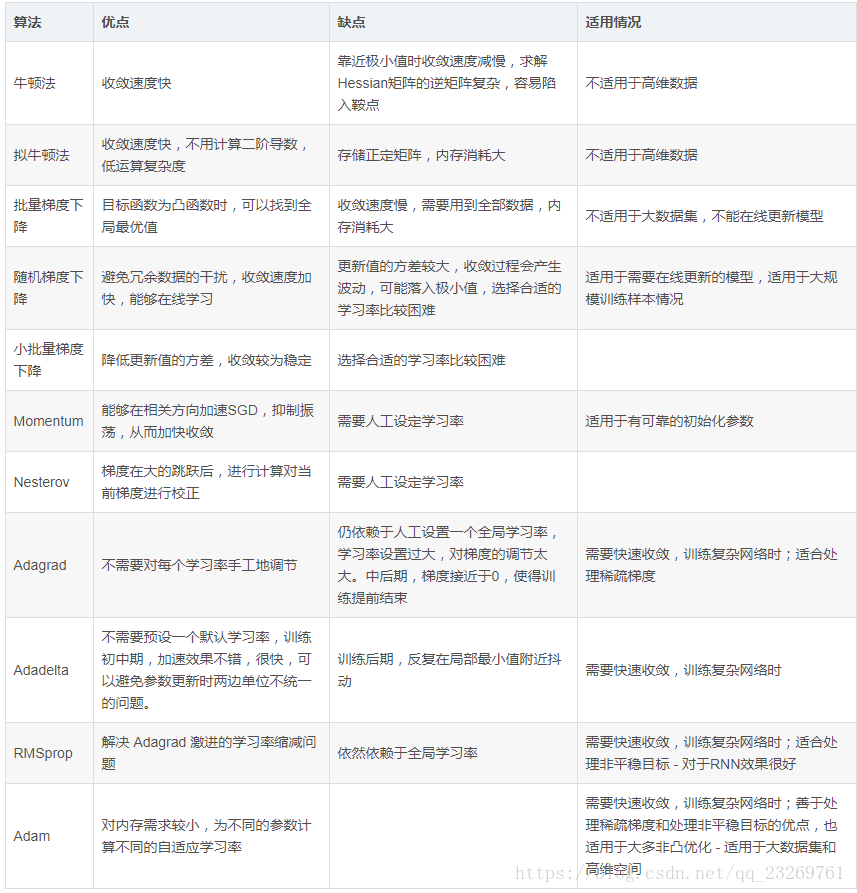
完。
感谢各位博主的分享,凡心所向,素履可往。