第二次结对作业

作者

031502500 林炜鸿

Github链接

项目地址

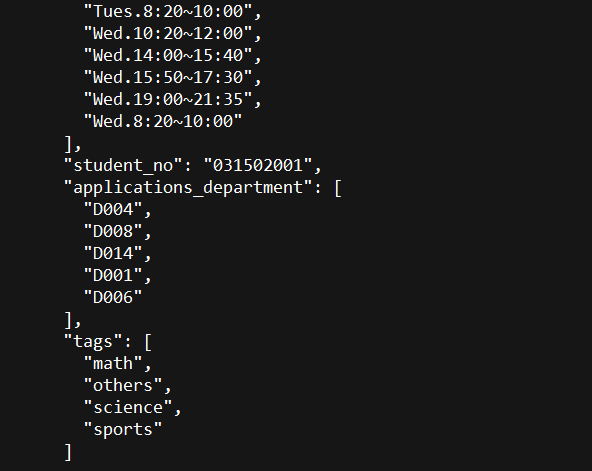
输入数据

input_data.txt

这组数据从结果上看没有unlucky_department
我们先是随机了所有部门的tags和event schedule，
之后又随机了所有学生的tags和free time
之后对每一个学生，遍历所有部门，并设一个参数NegScore反映出学生对每一个部门的喜爱程度
NegScore越小，则表示该学生越喜欢这个部门
在寻找的过程中，不断将时间冲突的部门用NegScore较小的那一个替换
确保此学生申请的所有部门互不冲突
最后对所有部门的NegScore排序，取最小的不超过5个的部门

建模过程

问题建模

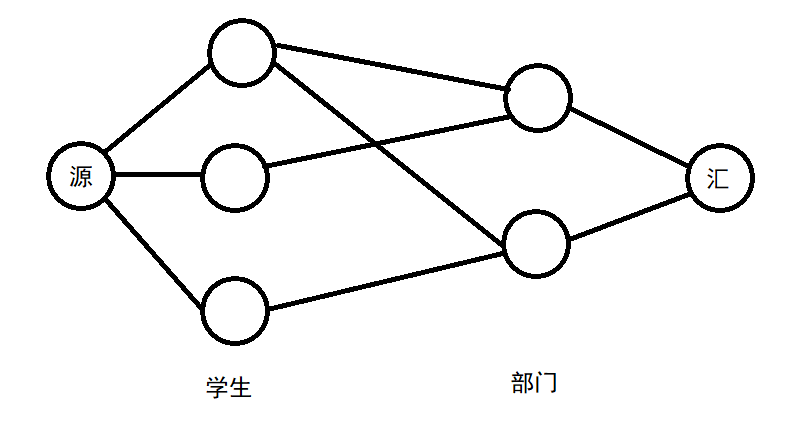
我们利用了最小费用最大流算法来解决此问题。
将所有学生和部门都抽象成图上的点。
流量即为通过部门申请的人次，费用即为所有学生的喜好程度的和。

算法实现

当A学生向B部门提出入部申请的时候，就从A向B连一条流量为1的边。
这条边容量为1，费用为这个B部门在A学生心目中的名次。
名次越高，费用越低，从而越可能选中这条边。
之后从源点向每个学生连一条流量为无穷，费用为0的边。
从每个部门向汇点连一条流量为该部门限定人数，费用为0的边。
之后在图上跑一遍费用流。
算法结束之后，如果A学生到B部门的边上有流量通过，则说明A加入了B部门。
所以只要遍历一下所有学生和部门之间的连边，检查边上的流量情况，就能获得所有部门的部员情况以及未能加入任一部门的学生和没有部员的部门。

代码规范

1. 利用较为详细的命名方法对变量，函数和对象进行命名。
   
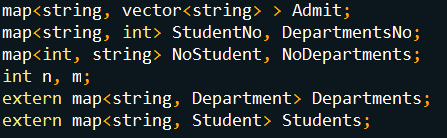
2. 对不需要修改的算法和函数进行封装。
   
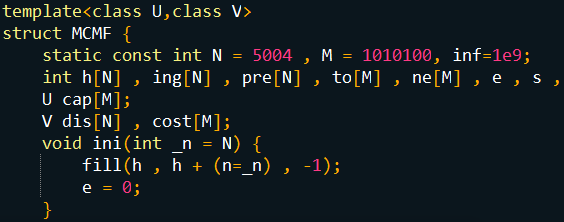
3. 利用C11新特性来简化对容器遍历的书写。
   

结果评估

此算法所能求出的最大人次，并非至少参与一个部门的学生的最大值（即unlucky_student的最小值），而是所有部门部员数总和的最大值。同时在此优化目标下，求出了全局权值最优的一个解。
这个算法的好处在于，能够简单地建立模型，实现算法，并且对问题得出一个合理的解。
这个算法的缺陷在于，不能处理一名学生申请的多个部门之间时间上互相冲突的情况。

最后一点感想

这次结队过程总体来说还是比较顺利的。经过上一次的磨合，编码前的讨论非常快的就完成了。确认好分工之后，就各自完成了自己的部分。浴盆同学代码能力了得，几乎没有什么bug，让人十分放心。我对于他代码里不懂的部分，也很耐心地解释给我听了，帅气地不行。虽然在编码过程中有一些编码风格的差异，但我觉得这并不是短期内能解决的。但是在一番努力和一些工具的帮助下，也总算能比较一致地规范代码风格了，最后看着40多小时写成的上百行的代码，还是很有成就感的。