
(1)
解题思路:
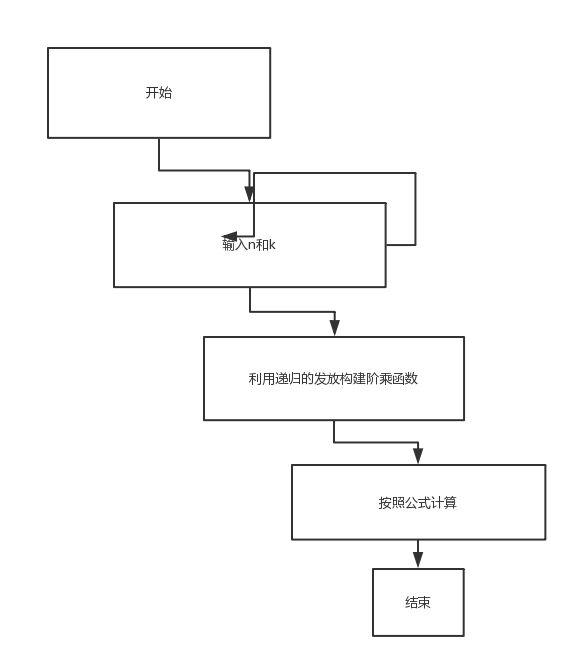
公式已经给出,利用递归的方法求阶乘,n为0和1时候为一,其他时候调用阶乘函数,利用递归方法求阶乘,然后按照公式计算结果。
流程图:
程序代码:
import java.util.Scanner;
public class zuheshu {
public static void main(String[] args){
System.out.println("请输入组合数的n和k");
@SuppressWarnings("resource")
Scanner cin=new Scanner(System.in);
int n,k;
n=cin.nextInt();
k=cin.nextInt();
while(k>n)
{
System.out.println("输入错误,请重新输入");
n=cin.nextInt();
k=cin.nextInt();
}
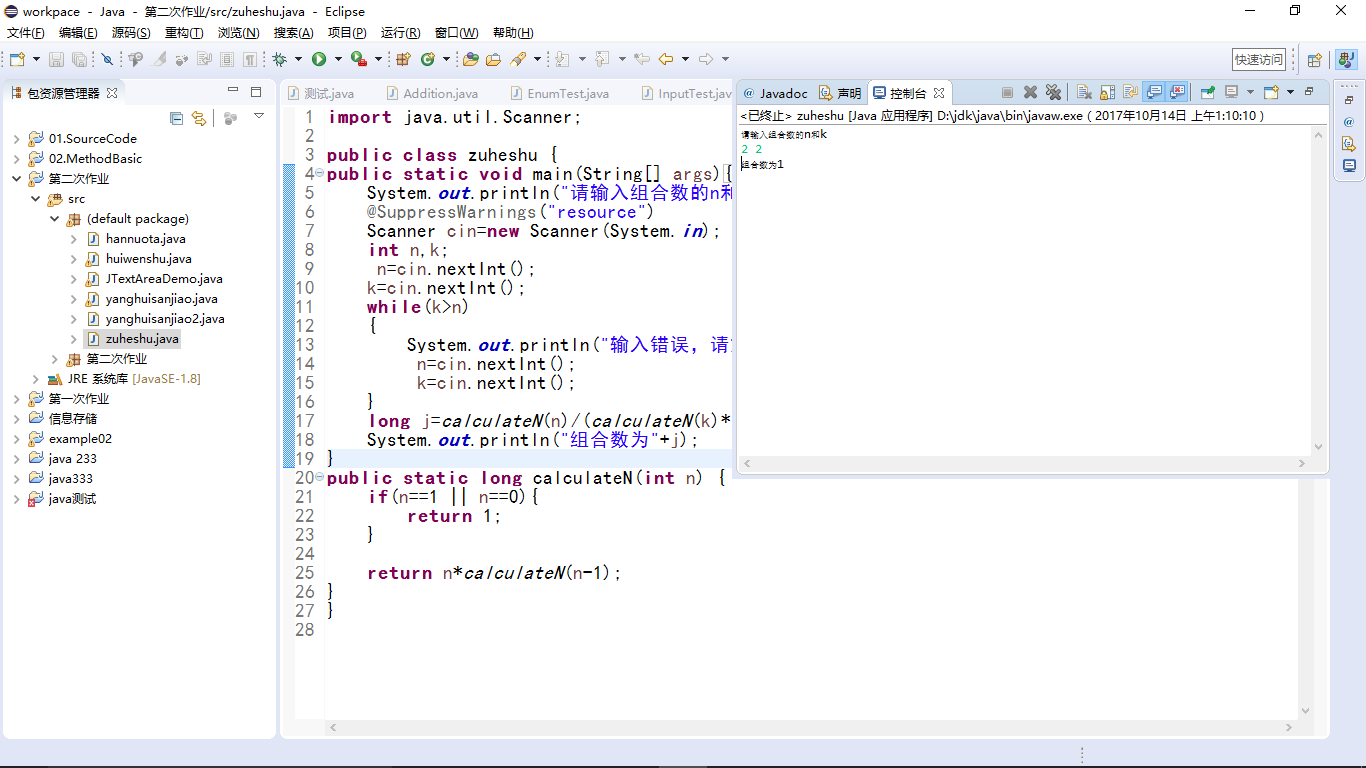
long j=calculateN(n)/(calculateN(k)*calculateN(n-k));//公式
System.out.println("组合数为"+j);
}
public static long calculateN(int n) {
if(n==1 || n==0){
return 1;
}
return n*calculateN(n-1);
}
}
截图:
:
(2)思路:
设置一个初始都为0的数组把数组的1 1 2 1 2 2都赋值为1,剩余按照公式的计算,然后按照数组的行和列来输出组合数。
流程图:

代码:
import java.util.Scanner;
public class yanghuisanjiao {
public static void main(String arg[]){
int a[][]=new int[100][100];
int i,j,n,k;
for(i=0;i<100;i++)
for(j=0;j<100;j++)
{
a[i][j]=0;
}//初始化
a[1][1]=1;
a[2][1]=1;
a[2][2]=1;//把前三个先赋值,便于后面的计算
for(i=3;i<100;i++)
for(j=1;j<100;j++)
{
a[i][j]=a[i-1][j-1]+a[i-1][j];//正常的按照数字来在数组中赋值就可以,以为0列都是0,后面的也是0
}
System.out.print("请输入组合数的n和k(即杨辉三角的行和列)");
Scanner cin=new Scanner(System.in);
n=cin.nextInt();
k=cin.nextInt();
while(k>n)//防止出错
{
System.out.println("输入错误,请重新输入");
n=cin.nextInt();
k=cin.nextInt();
}
System.out.println("组合数为"+a[n][k]);
}
}
截图:
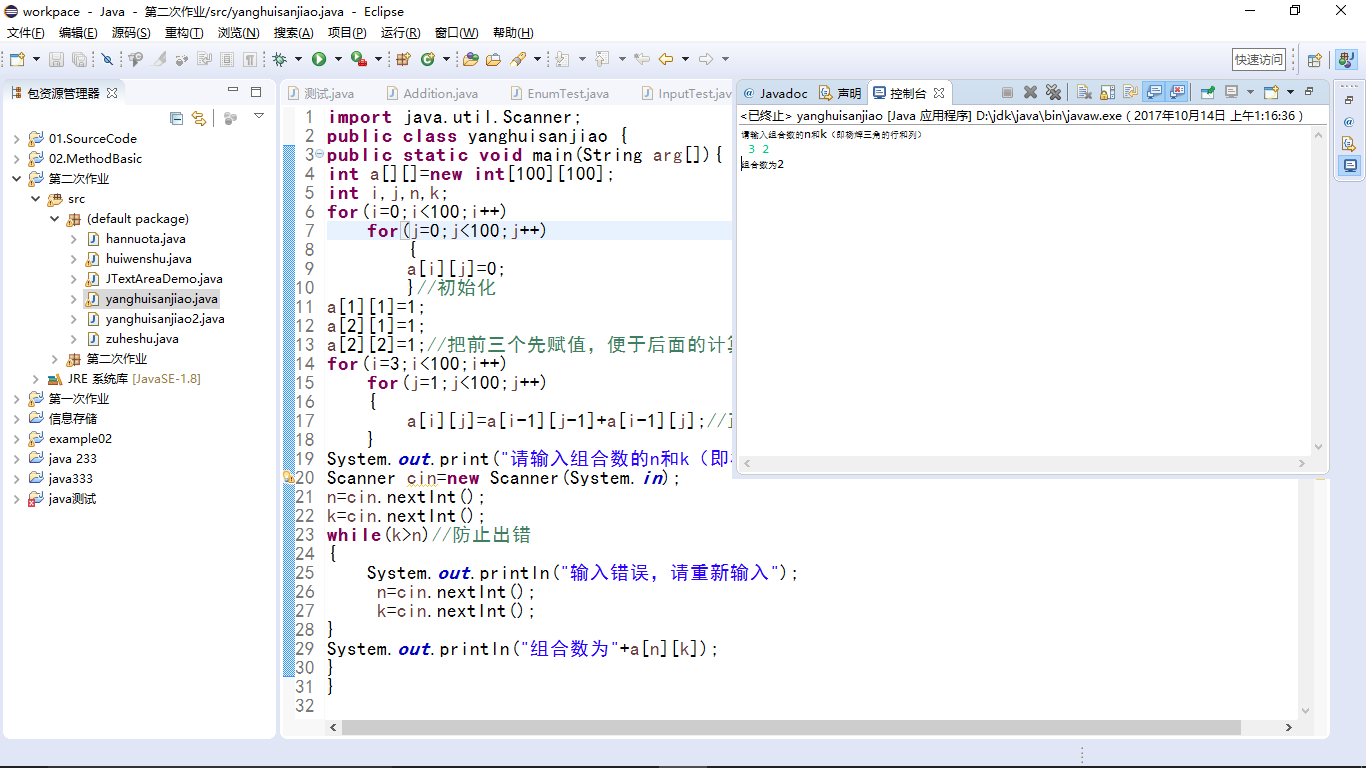
(3)
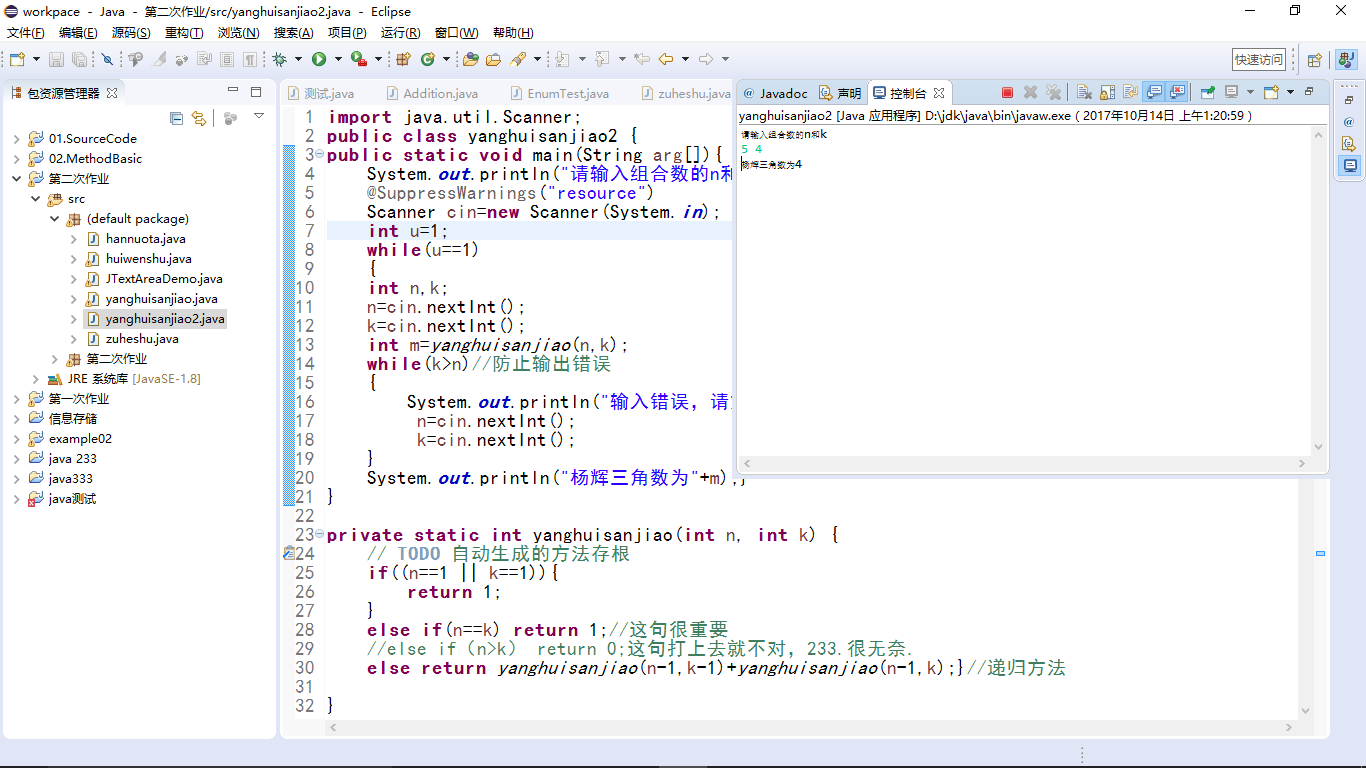
思路:利用递归的思想和题目中给的公式,递归方法中,当行列为1 1时候返回1,行和列相等时候返回1,其余利用递归方法求。
流程图:
代码:
import java.util.Scanner;
public class yanghuisanjiao2 {
public static void main(String arg[]){
System.out.println("请输入组合数的n和k");
@SuppressWarnings("resource")
Scanner cin=new Scanner(System.in);
int u=1;
while(u==1)
{
int n,k;
n=cin.nextInt();
k=cin.nextInt();
int m=yanghuisanjiao(n,k);
while(k>n)//防止输出错误
{
System.out.println("输入错误,请重新输入");
n=cin.nextInt();
k=cin.nextInt();
}
System.out.println("杨辉三角数为"+m);}
}
private static int yanghuisanjiao(int n, int k) {
// TODO 自动生成的方法存根
if((n==1 || k==1)){
return 1;
}
else if(n==k) return 1;//这句很重要
//else if(n>k) return 0;这句打上去就不对,233.很无奈.
else return yanghuisanjiao(n-1,k-1)+yanghuisanjiao(n-1,k);}//递归方法
}
截图:
思路:
利用递归的方法,每次移动给一个盘子,而且大盘子必须在小盘子下面,三根柱子一根作为辅助 ,把盘子从一个一定到另一个柱子,所以利用递归求移动的次数,并且创建一个move函数显示移动轨迹。
流程图:
代码:
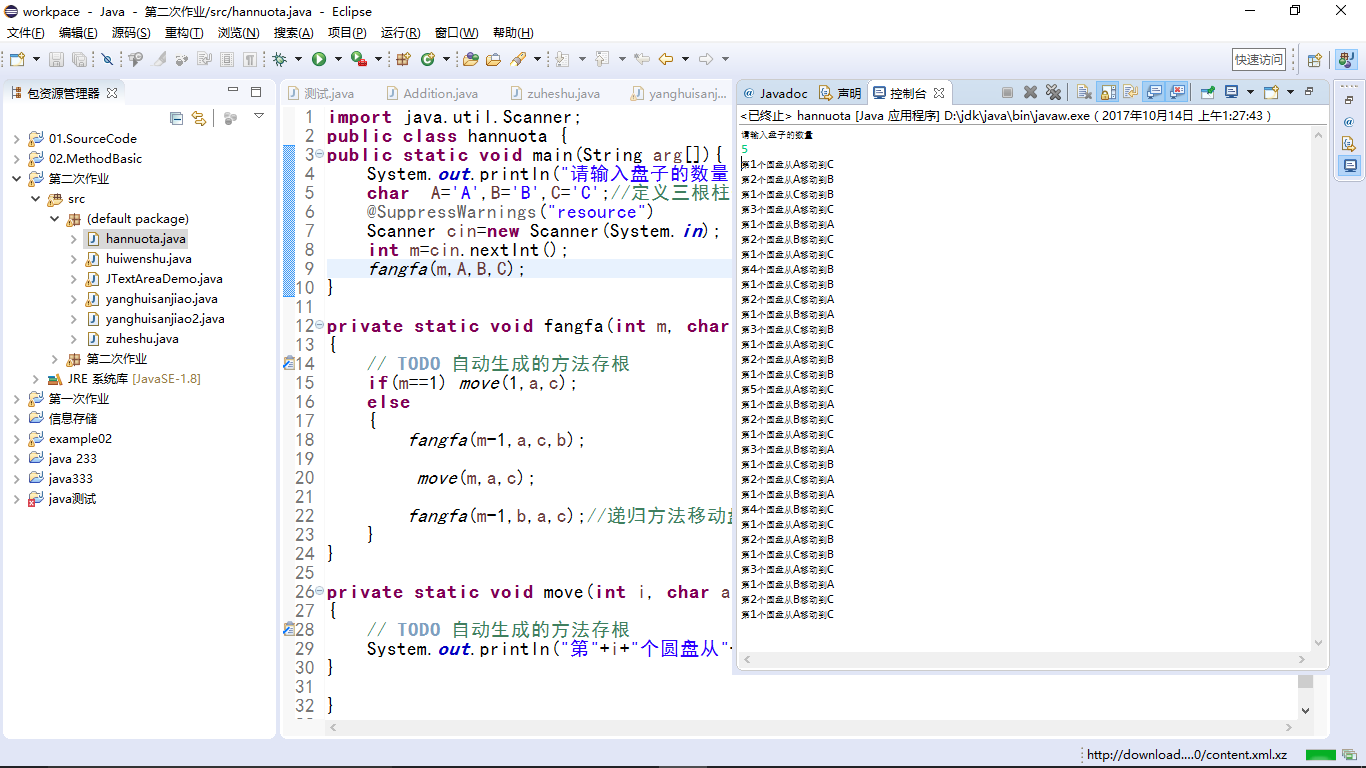
import java.util.Scanner;
public class hannuota {
public static void main(String arg[]){
System.out.println("请输入盘子的数量");
char A='A',B='B',C='C';//定义三根柱子
@SuppressWarnings("resource")
Scanner cin=new Scanner(System.in);
int m=cin.nextInt();
fangfa(m,A,B,C);
}
private static void fangfa(int m, char a, char b, char c)//b做辅助,把m个盘子从a移动到c
{
// TODO 自动生成的方法存根
if(m==1) move(1,a,c);
else
{
fangfa(m-1,a,c,b);
move(m,a,c);
fangfa(m-1,b,a,c);//递归方法移动盘子
}
}
private static void move(int i, char a, char c)//输出盘子移动的函数
{
// TODO 自动生成的方法存根
System.out.println("第"+i+"个圆盘从"+a+"移动到"+c);
}
}
截图:

思路:
定义一个string类型的数据,从键盘输入然后用递归的方法 依次比较字符串的第一个字符与最后一个是否相等。
流程图:

代码:
import java.util.Scanner;
public class huiwenshu {
public static void main(String agr[]){
Scanner cin=new Scanner(System.in);
System.out.println("请输入字符");
String j=cin.next();
int m,n;
m=0;//字符串的第一个字符
n=j.length()-1;//字符串的最后一个字符
palindrome(j,m,n);//判断回文数的函数
}
private static void palindrome(String j, int m, int n) {
// TODO 自动生成的方法存根
if(m==n) System.out.println("是回文数");
else if(m==n-1) System.out.println("是回文数");
else if (j.charAt(m)==j.charAt(n))//判断两个字符是否相等
{palindrome(j,m+1,n-1);}
else System.out.println("不是回文数");
}
}
截图:

心得体会:
这几个都是用调用的递归方法的函数来实现程序的,让我对java
的递归方法有了更全面的了解,但是有的递归的最先条件非常不好判断,还学会了string 的字符比较方法。