Programming Assignment 1: Percolation

编程作业一

作业链接：Percolation & Checklist

我的代码：Percolation.java & PercolationStats.java

编程解决上篇博客 Union-Find 最后提到的渗透问题（Percolation），写个电脑程序来估计阈值 p* 。

任务摘要

Percolation Data Type

To model a percolation system, create a data type Percolation with the following API:

public class Percolation {
   public Percolation(int n)                // create n-by-n grid, with all sites blocked
   public void open(int row, int col)       // open site (row, col) if it is not open already
   public boolean isOpen(int row, int col)  // is site (row, col) open?
   public boolean isFull(int row, int col)  // is site (row, col) full?
   public int numberOfOpenSites()           // number of open sites
   public boolean percolates()              // does the system percolate?

   public static void main(String[] args)   // test client (optional)
}

Mote Carlo Simulation

To perform a series of computational experiments, create a data type PercolationStats with the following API.

public class PercolationStats {
  public PercolationStats(int n, int trials)    // perform trials independent experiments on an n-by-n grid
  public double mean()                          // sample mean of percolation threshold
  public double stddev()                        // sample standard deviation of percolation threshold
  public double confidenceLo()                  // low  endpoint of 95% confidence interval
  public double confidenceHi()                  // high endpoint of 95% confidence interval

  public static void main(String[] args)        // test client (described below)
}

详细的要求参见：Percolation。

问题分析

1. Percolation Data Type

任务一要我们创建一个数据结构来表示渗透系统，包含判断方块是否打开，打开方块等方法。有了课程里的想法，基本上不需要多想，想太多反而无从下手，直接一个个实现，错了再改就好。

值得一提的是 isFull() 这个方法。连通区域里的白色方块才是 full，就是下图中蓝色的方块。

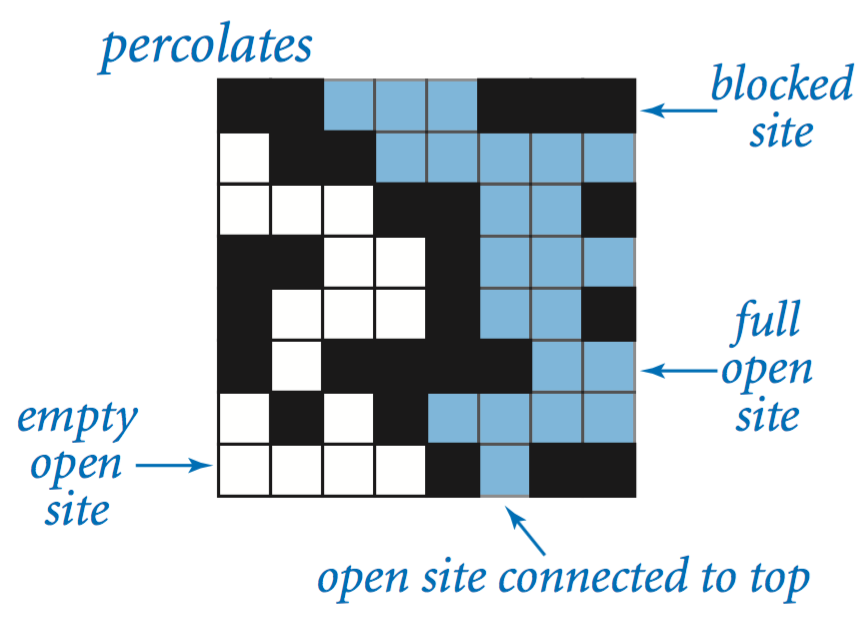
很自然地想到方块 full 需要满足系统渗透且处在连通区域里这两个条件，但存在一个 Checklist 里提到的 backwash 问题。backwash 这些方块从图像上看不在连通区域里，却会被断定为 full 。

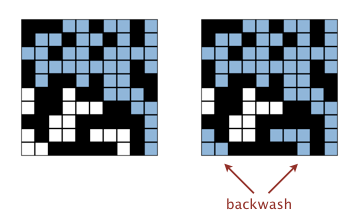
因为我们虚拟了两个方块来简化判断系统是否渗透的问题，其实 backwash 这些白色方块在并查集里也会被并入连通区域。

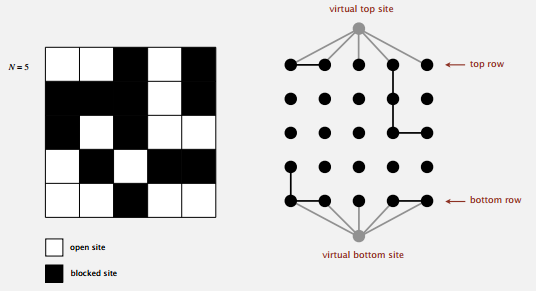
这对下面的蒙特卡罗模拟实验倒没有影响，因为实验需要的是系统渗透时白色方块的数目，而不是 full 方块的数目。Checklist 里也说不用太纠结这个，所以我一开没看懂也就不管了，但最后代码交上去却显示判断方法有些测试没过。。。

It is only a minor deduction (because it impacts only the visualizer and not the experiment to estimate the percolation threshold), so don't go crazy trying to get this detail. However, many students consider this to be the most challenging and creative part of the assignment (especially if you limit yourself to one union-find object).

Checklist 提示不要限制在只使用一个并查集上，稍加思索，那我就再来一个。

于是，又虚拟了一个“上面的方块2.0”，一样和第一行所有白色方块相连。在这个并查集里， 没有下面的虚拟方块作媒介，backwash 是不会和“上面的方块2.0”相连的。系统渗透且和“上面的方块2.0”相连，那么这个方块就一定是 full 的啦。再提交上去，isFull() 的测试全过，成功解决了这个问题。但是，又出现了新的问题：超出了限制的使用内存。。。

盯着代码看来看去，最后把 private byte[][] grid; // 0 means block , 1 means open 的 int 改成 bite 。。。通过了所有测试点！Github: Percolation.java。因为是在课程结束后才写的博客，原来没有传到 Github 上，所以没有什么提交记录。此外，Checklist 里提供的用来测试的代码和数据也是很有趣，这里贴些我跑的。

PercolationVisualizer.java

输入文件：greeting57.txt。

InteractivePercolationVisualizer.java

可以看到左下角那些 backwash 方块没有被误判为 full。

2. Mote Carlo Simulation

模拟程序问题不大，直接贴我的实现：PercolationStats.java。

测试结果

课程结束才写的博客，发现结束的课程编程作业会被锁起来，看不了评测细节，于是又注册了小号加入课程提交代码，哈哈哈哈。