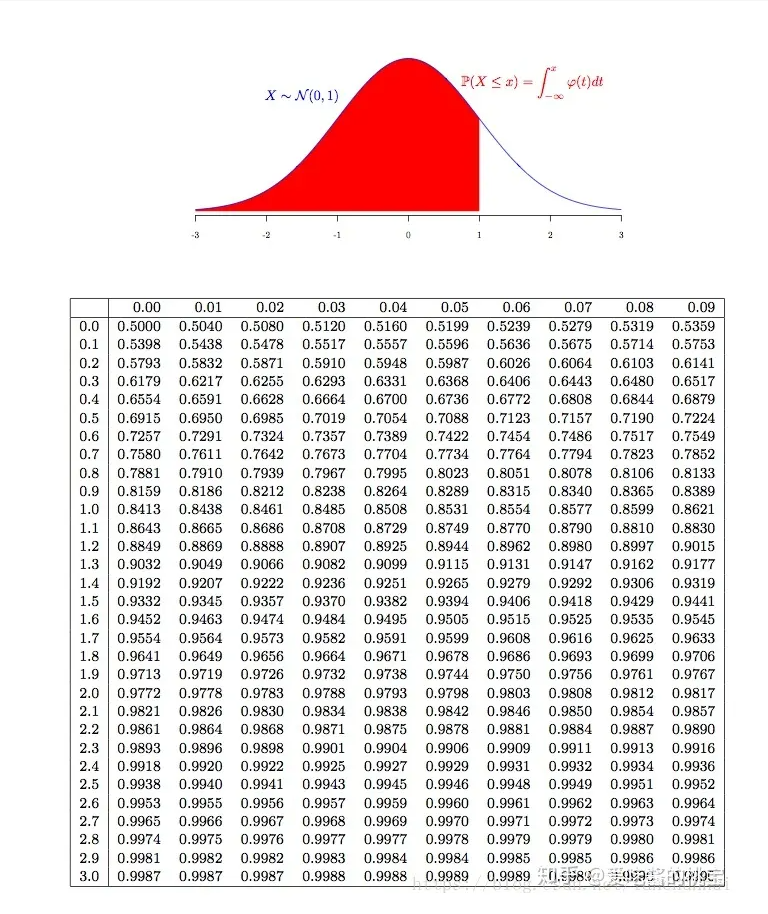
学习备忘内容来自:普通正态分布如何转换到标准正态分布
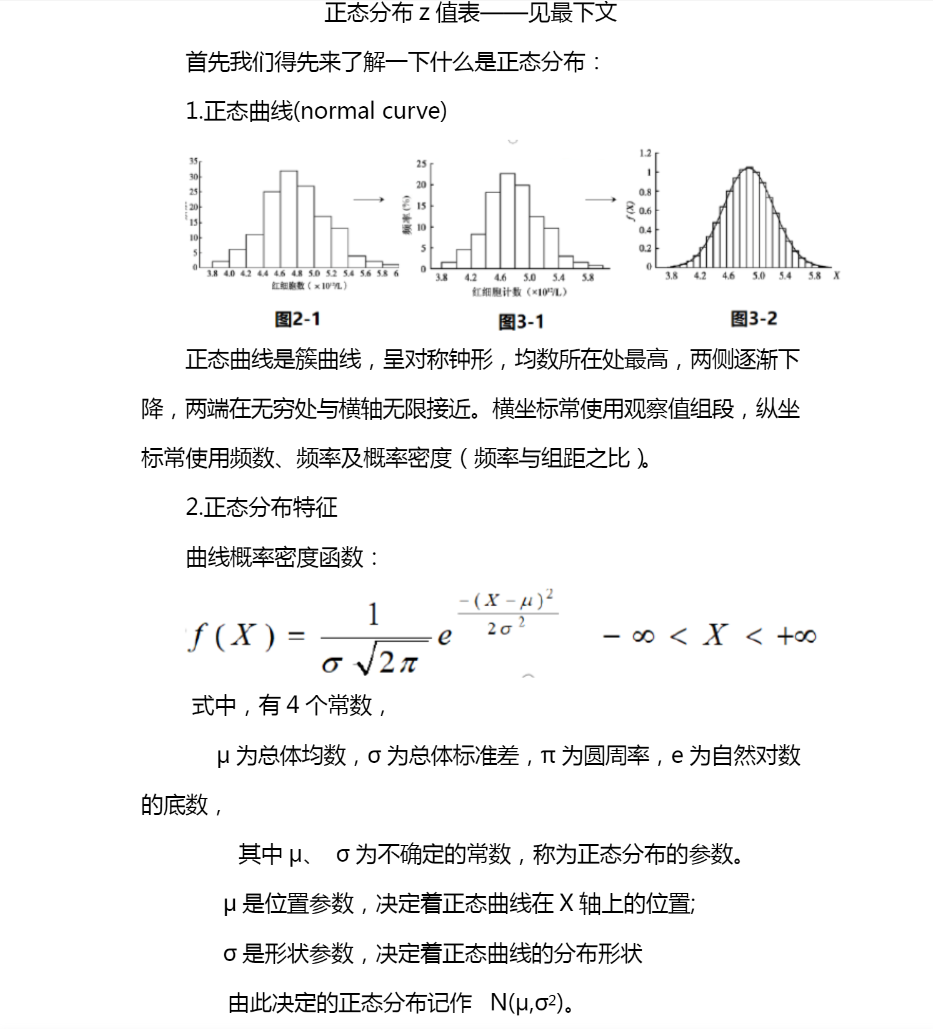
一般用N(μ,σ2)表示均数为μ,方差为σ2的正态分布。
如何判断一组数据是否符合正态分布



3.几个应用的例子
3.1 假设公共汽车门的高度按成年男性碰头机会小于1%来设计。又假设成年男性的身高服从正态分布X ∼ N ( 170 , 6 2 ) X \sim N(170, 6^2)X∼N(170,6
2
),求问车门的高度h hh为多少?
假设身高这一随机变量为X XX,那么要求的问题为:
P ( x > h ) = 0.01 P(x > h) = 0.01
P(x>h)=0.01
即
1 − P ( x ≤ h ) = 0.01 1 - P(x \le h) = 0.01
1−P(x≤h)=0.01
P ( x ≤ h ) = 0.99 P(x \le h) = 0.99
P(x≤h)=0.99
因为X ∼ N ( 170 , 6 2 ) X \sim N(170, 6^2)X∼N(170,6
2
), 所以h − 170 6 ∼ N ( 0 , 1 ) \frac{h - 170}{6} \sim N(0, 1)
6
h−170
∼N(0,1)。
通过查标准正态分布表可知,P ( z ≤ 2.33 ) = 0.99 P(z \le 2.33) = 0.99P(z≤2.33)=0.99
因此h = 170 + 6 * 2.33 = 183.98cm
3.2 现在有一个μ = 10 \mu = 10μ=10和σ = 2 \sigma = 2σ=2的正态随机变量,求x在10与14之间的概率是多少?
当x=10时,z = 0。当x=14时,z = (14-10)/2 = 2。于是,x在10与14之间的概率等价于标准正态分布中0与2之间的概率。
P ( 0 ≤ z ≤ 2 ) = P ( z ≤ 2 ) − P ( z ≤ 0 ) = 0.4772 P(0 \le z \le 2) = P(z \le 2) - P(z \le 0) = 0.4772
P(0≤z≤2)=P(z≤2)−P(z≤0)=0.4772