堆排序

与归并排序一样，但不同于插入排序，堆排序的时间复杂度为O(nlgn)。与插入排序一样，但不同于归并排序，堆排序具有空间原始性，即排序过程中只需要常数个额外的元素空间来存储临时数据。

1、堆是一个数组，它可以看成一个近似的完全二叉树，树上的每个节点对应着数组中的每个元素。对于一个给定下标为 i 的元素  ,可以很容易的计算出它的父节点，左孩子和右孩子的下标。

   

        

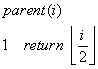
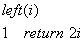
2、堆又分为两种，最大堆和最小堆。最大堆的性质:除了根节点外，其余节点要满足条件A[parent(i)]≥A[i]。最小堆的性质:除了根节点外，其余节点要满足条件A[parent(i)]≤A[i]。

3、下面是基于最大堆的堆排序过程。

　　基本过程：

　　　　MAX-HEAPIFY过程：用于维护最大堆的性质 即A[parent(i)]≥A[i]。时间复杂度为Ο(lgn)。

　　　　BUILD-MAX-HEAP过程：功能是将一个无序数组构造为一个最大堆的过程。时间复杂度为Ο(n)。

　　　　HEAPSORT过程:其功能是对一个数组进行原址排序。时间复杂度为Ο(nlgn)。

4、MAX-HEAPIFY过程，维护最大堆性质

　　在调用MAX-HEAPIFY(A,i)过程的时候，假设前提根节点为left(i)和right(i)的二叉树都是最大堆，但这时A[i]可能小于其孩子left(i)和right(i)，这就违背了最大堆的性质。通过调用MAX-HEAPIFY过程，可以使得根节点为i的二叉树为最大堆。

　　伪代码如下图：

MAX-HEAPITY(A,i)
1    l = left(i)
2    r = right(i)
3    if(l <= A.heap-size && A[i] < A[l])
4        largest = l
5    else largest = i
6    if(r <= A.heap-size && A[largest] <A[r])
7        largest = r
8    if(largest != i)
9        exchange A[largest] with A[i]
10       MAX-HEAPITY(A,largest)

 　　

　　下图展示了MAX-HEAPIFY过程。

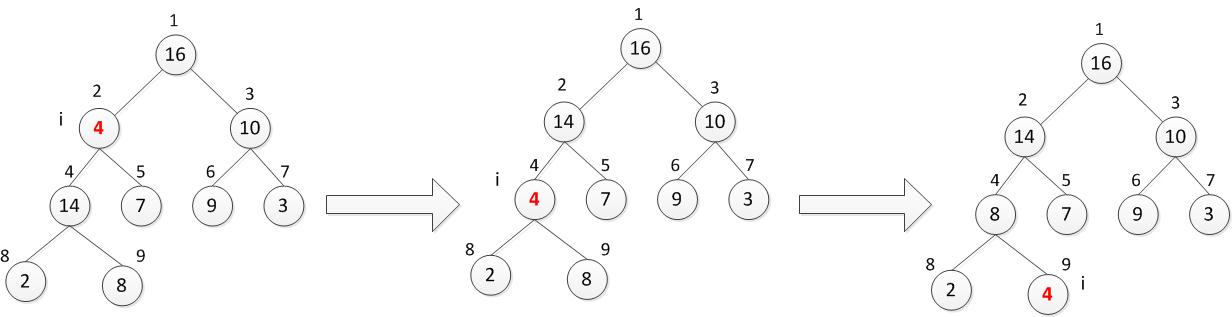
　　上图中，以i的孩子left(i)和right(i)为根节点的二叉树都是最大堆，但是A[i]小于left[i]和right[i]，所以A[i]为根节点的二叉树不是最大堆，调用MAX-HEAPIFY过程，将数组转换为一个最大堆。

　　 对于一颗以i为根节点，大小为n的堆，MAX-HEAPIFY过程的时间代价为T(n)，其中包括：伪代码1-9行时间代价为θ(1)，假设8行条件成立，则会调用10行的递归过程。因为每个孩子的子树大小至多为2n⁄3（最坏情况发生在最底层恰好为半满的时候），所以10行时间代价小于等于T(2n/3)。因此MAX-HEAPIFY过程的时间代价 T(n)<=T(2n/3)+θ(1)。利用递归式主方法，上面递归式的解为T(n)=O(lgn)。一个含有n个元素的堆，堆高度h=θ(lgn)，所以对一个树高度为h的节点来说，MAX-HEAPIFY过程的时间复杂度为O(h)。

5、BUILD-MAX-HEAP过程，建堆

　　建堆的过程是将一个大小为n=A.length的数组A[1,2,...,n]转换为最大堆的过程。从底层第一个有孩子的节点开始，自低向上的逐个节点调用MAX-HEAPIFY过程，直到最顶层根节点为止。下标为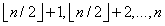的元素都是树的叶节点，过程BUILD-MAX-HEAP对树中的其他节点都调用一次MAX-HEAPIFY。下面是BUILD-MAX-HEAP过程的伪代码：

BUILD-MAX-HEAP(A)
1    A.heap-size = A.length
2    for i = floor(A.length/2) downto 1　　//floor为向下取整
3        MAX-HEAPIFY(A,i)

下图为BUILD-MAX-HEAP过程的例子

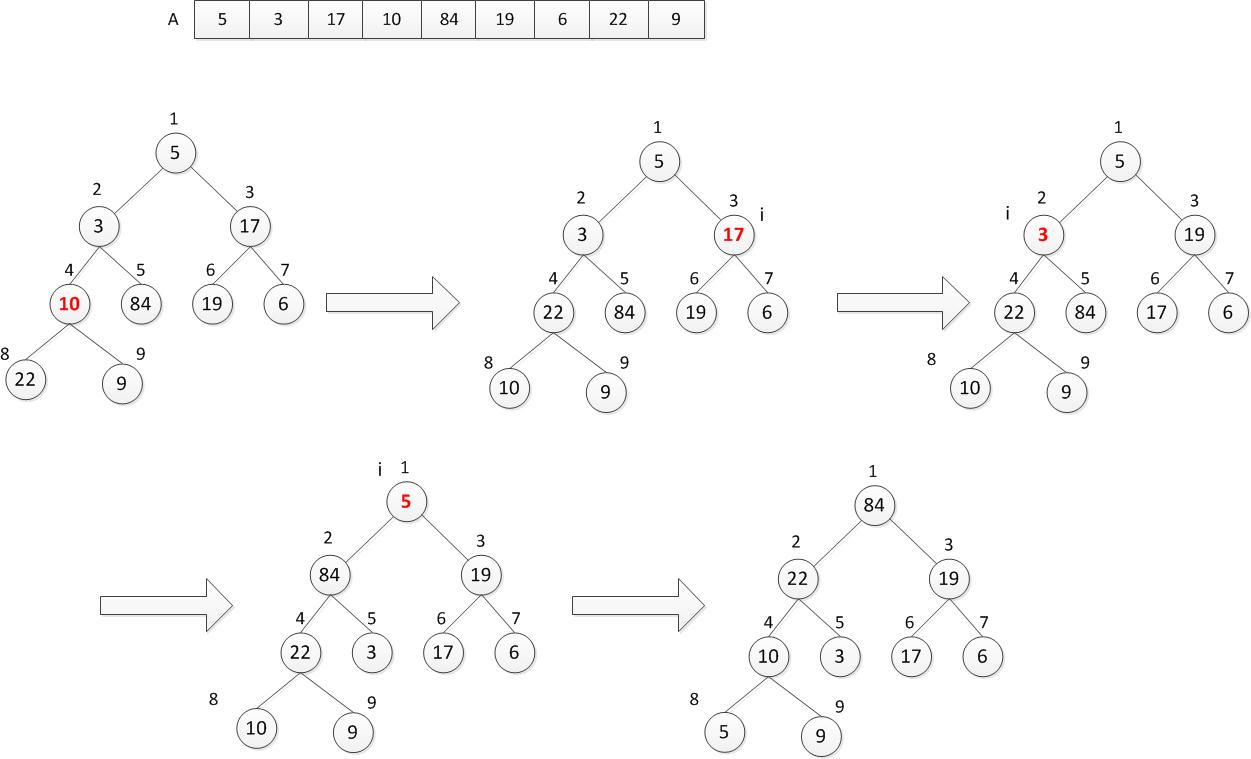
　　BUILD-MAX-HEAP过程的时间代价为O(n)。

　　每次调用MAX-HEAPIFY(A,i)过程的时间代价为O(lgn)，BUILD-MAX-HEAP过程中，round(A.length/2) downto 1总共有O(n)次调用MAX-HEAPIFY(A,i)过程。所以直观上BUILD-MAX-HEAP过程总的时间复杂度为O(nlgn)。

　　但MAX-HEAPIFY(A,i)过程的时间代价与高度h有关系，并且大多数节点的高度都很小，所以可以计算出更为精确的上界。利用如下性质：1、含有n个元素的堆的高度为floor(lgn) (注：floor为向下取整)；2、对于任一包含n个元素的堆中，至多有ceil(n/2^h+1) (注：ceil为向上取整)个高度为h的节点。

　　BUILD-MAX-HEAP过程的时间代价可以表示为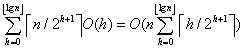：，又有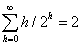，所以有BUILD-MAX-HEAP过程的时间复杂度为：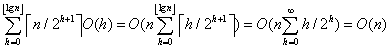

6、HEAPSORT过程（堆排序算法）

HEAPSORT(A)
1    BUILD-MAX-HEAP(A)
2    for i = A.length dowto 2
3        exchange A[i] with A[1]
4        A.heap-size = A.heap-size-1
5        MAX-HEAPIFY(A,1)

　　

　　首先将数组A转换为一个最大堆，此时数组A中的最大元素肯定位于堆的根节点A[1]，通过根节点A[1]与节点A[n]的交换，可以将A[1]放到正确的位置。这时候，通过 A.heap-size = A.heap-size-1 操作将节点A[n]从堆中去掉，剩余的节点中，A[1]的两个孩子均为最大堆的根节点，但是A[1]可以小于它的孩子，因此调用MAX-HEAPIFY(A,1)过程，使得A[1,2,...,n-1]转换为最大堆。下图为HEAPSORT的一个例子。

　　堆排序的时间复杂度为O(nlgn)。BUILD-MAX-HEAP(A)过程的时间代价为O(n)，n-1次调用MAX-HEAPIFY的时间代价为O(nlgn)，所以堆排序的时间复杂度为O(nlgn)。