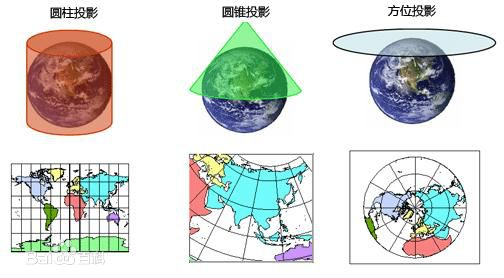
一、坐标系统:
坐标系统是描述物质存在的空间位置(坐标)的参照系,通过定义特定基准及其参数形式来实现。坐标是描述位置的一组数值。按坐标的维度分为一维坐标(公路里程碑)和二维(笛卡尔平面直角坐标。高斯平面直角坐标)、三维坐标(大地坐标、空间直角坐标)。为了描述或确定位置,必须建立坐标系统,坐标只有存在于某个坐标系统才有实际的意义于具体的位置。
在研究地理空间的组成对象及其相互关系时,首先必须确定过该空间的参考体系。地理空间坐标系的建立目的就在于确定任意一个地面店的位置,这包括它在大地水准面上的平面位置以及它到大地水准面的高程。平面位置可由经纬度给定。因为地理空间坐标系是球面坐标系,难以进行距离、方向、面积等参数的计算,实际研究中也不够直观,因此理想的办法就是将球面对象映射到平面笛卡尔坐标系上,地图投影正式按照一定的数学法则实现这种变换。
二、ArcGIS中的坐标系
ArcGIS中坐标系统有两种:地理坐标系和投影坐标系。
1.地理坐标系(Geographic coordinate system)
地理空间坐标系使用经纬度坐标来描述地球上某一点所处的位置。
地理坐标系坐标经度范围(-180-180),纬度(-90-90);
地理坐标系以度为单位;
地理坐标系:为球面座标,参考平面地是椭球面,坐标单位:经纬度。
2.投影坐标系(Projecetion coordinate system)
使用基于X,Y值得坐标系统来描述地球上某个点所处的位置。这个坐标系是从地球的近似椭球体投影得到的,它对应于某个地理坐标系。平面坐标系统地图单位通常为米,或者是平面直角坐标。
投影坐标系由以下两项参数确定:
地理坐标系:由基准面决定(北京54、西安80、WGS84)
投影方法:(高斯克吕格、Lambert投影)
坐标是GIS数据的骨骼框架,能够将我们的数据定位到相应的位置;为地图中的每一点提供准确地数据。
3.投影方法介绍:
1)Lambert等角圆锥投影:
用于小比例的地图投影如1:50万,1:100万,1:400万等小比例尺,经线为辐射直线,纬线为同心圆圆弧。指定两条标准纬度线Q1,Q,在这两条纬度线上没有长度变形,即M=N=1.此种投影也叫等角割圆锥投影。
正轴等角割圆锥投影又称为兰伯特正形圆锥投影,由德国数学家兰伯特(J.H..Lambert)提出。这种投影是将一圆锥面套在地球椭球体外面,将地球表面上的要素投影到圆锥面上,然后将圆锥面元沿着某一条经线展开,即获得Lambert投影。
https://baike.baidu.com/item/正轴等角割圆锥投影/16177276?fr=aladdin
兰伯特等角圆锥投影、高斯-克吕格投影、UTM投影、
http://www.cehui8.com/zhuanti/map/20130701/192.html
(2)高斯—克吕格投影方法
又名"等角横切椭圆柱投影”,是地球椭球面和平面间正形投影的一种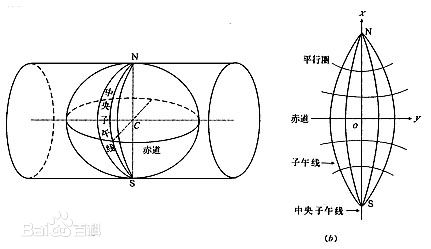
高斯克吕格投影这一投影的几何概念是,假想有一个椭圆柱与地球椭球体上某一经线相切,其椭圆柱的中心轴与赤道平面重合,将地球椭球体面有条件地投影到椭球圆柱面上高斯克吕格投影条件:a) 中央经线和赤道投影为互相垂直的直线,且为投影的对称轴; b) 具有等角投影的性质; c) 中央经线投影后保持长度不变;
如图所示,假想有一个椭圆柱面横套在地球椭球体外面,并与某一条子午线(此子午线称为中央子午线或轴子午线)相切,椭圆柱的中心轴通过椭球体中心,然后用一定投影方法,将中央子午线两侧各一定经差范围内的地区投影到椭圆柱面上,再将此柱面展开即成为投影面,如图2所示,此投影为高斯投影。高斯投影是正形投影的一种。
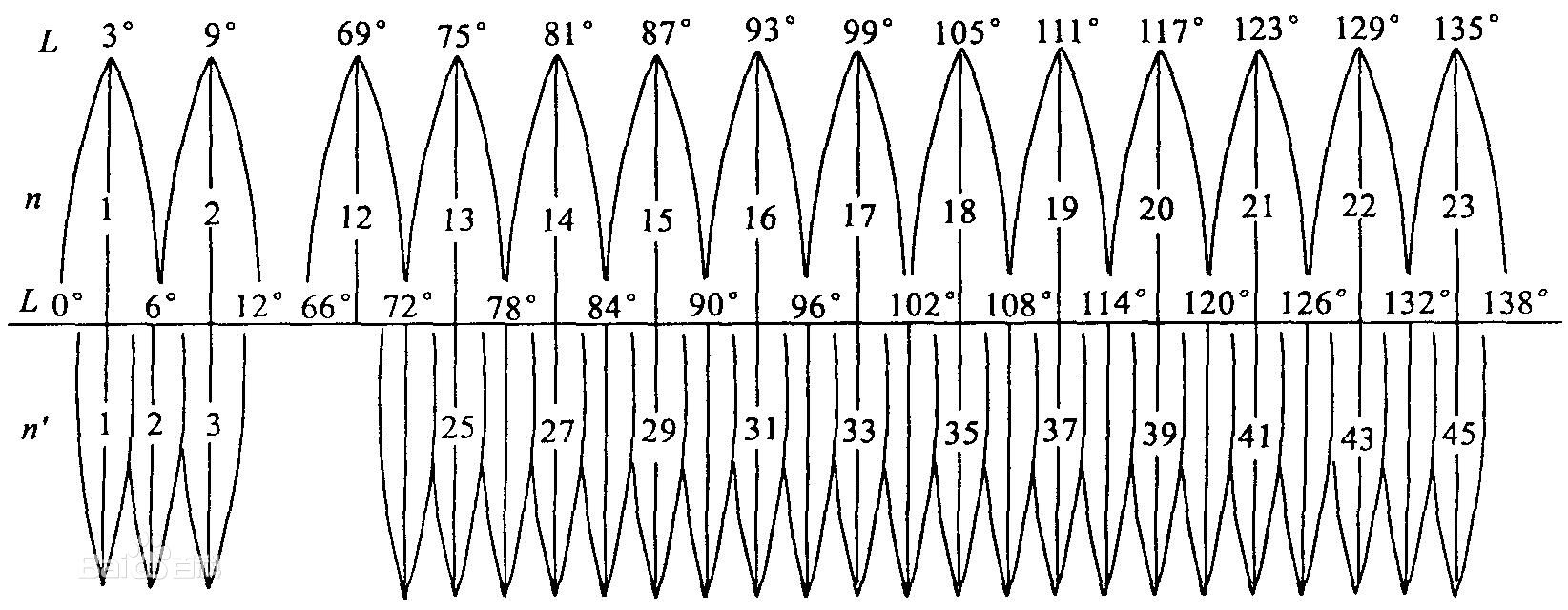
(2) 按一定经差将地球椭球面划分成若干投影带,这是高斯投影中限制长度变形的最有效方法。分带时既要控制长度变形使其不大于测图误差,又要使带数不致过多以减少换带计算工作,据此原则将地球椭球面沿子午线划分成经差相等的瓜瓣形地带,以便分带投影。通常按经差6度或3度分为六度带或三度带。六度带自0度子午线起每隔经差6度自西向东分带,带号依次编为第 1、2…60带。三度带是在六度带的基础上分成的,它的中央子午线与六度带的中央子午线和分带子午线重合,即自 1.5度子午线起每隔经差3度自西向东分带,带号依次编为三度带第 1、2…120带。我国的经度范围西起 73°东至135°,可分成六度带十一个,各带中央经线依次为75°、81°、87°、……、117°、123°、129°、135°,或三度带二十二个。六度带可用于中小比例尺(如 1:250000)测图,三度带可用于大比例尺(如 1:10000)测图,城建坐标多采用三度带的高斯投影。
高斯- 克吕格投影是按分带方法各自进行投影,故各带坐标成独立系统。以中央经线投影为纵轴(x), 赤道投影为横轴(y),两轴交点即为各带的坐标原点。纵坐标以赤道为零起算,赤道以北为正,以南为负。我国位于北半球,纵坐标均为正值。横坐标如以中央经线为零起算,中央经线以东为正,以西为负,横坐标出现负值,使用不便,故规定将坐标纵轴西移500公里当作起始轴,凡是带内的横坐标值均加 500公里。由于高斯-克吕格投影每一个投影带的坐标都是对本带坐标原点的相对值,所以各带的坐标完全相同,为了区别某一坐标系统属于哪一带,在横轴坐标前加上带号,如(4231898m,21655933m),其中21即为带号。
(4)UTM投影
高斯-克吕格投影与UTM投影
某些国外的软件如ARC/INFO或国外仪器的配套软件如多波束的数据处理软件等,往往不支持高斯-克吕格投影,但支持UTM投影,因此常有把UTM投影坐标当作高斯-克吕格投影坐标提交的现象。
UTM投影全称为“通用横轴墨卡托投影”,是等角横轴割圆柱投影(高斯-克吕格为等角横轴切圆柱投影),圆柱割地球于南纬80度、北纬84度两条等高圈,该投影将地球划分为60个投影带,每带经差为6度,已被许多国家作为地形图的数学基础。UTM投影与高斯投影的主要区别在南北格网线的比例系数上,高斯-克吕格投影的中央经线投影后保持长度不变,即比例系数为1,而UTM投影的比例系数为0.9996。UTM投影沿每一条南北格网线比例系数为常数,在东西方向则为变数,中心格网线的比例系数为0.9996,在南北纵行最宽部分的边缘上距离中心点大约 363公里,比例系数为 1.00158。
高斯-克吕格投影与UTM投影可近似采用 Xutm=0.9996 * X高斯,Yutm=0.9996 * Y高斯进行坐标转换。以下举例说明(基准面为WGS84):
输入坐标(度) 高斯投影(米) UTM投影(米) Xutm=0.9996 * X高斯, Yutm=0.9996 * Y高斯 纬度值(X)32 3543600.9 3542183.5 3543600.9*0.9996 ≈ 3542183.5 经度值(Y)121 21310996.8 311072.4 (310996.8-500000)*0.9996+500000 ≈ 311072.4
注:坐标点(32,121)位于高斯投影的21带,高斯投影Y值21310996.8中前两位“21”为带号;坐标点(32,121)位于UTM投影的51带,上表中UTM投影的Y值没加带号。因坐标纵轴西移了500000米,转换时必须将Y值减去500000乘上比例因子后再加500000。
单点转换步骤如下:
(1)选择是高斯正转换还是反转换,缺省为经纬度转换到高斯投影坐标,投影坐标单位为米。
(2)选择大地基准面,缺省北京54,如果是GPS定位数据别忘了切换为WGS84。
(3)选择分带,3度或6度, 缺省为6度。
(4)输入中央经度,20带(114°E~120°E)中央经度为117度,21带(120°E~126°E)中央经度为123度。
(5)如正向投影,选择经纬度输入数据格式,有三个选项,缺省为十进制度格式。具体输入方式如下例:
格 式 原始纬度值 原始经度值 输入纬度值 输入经度值 十进制度 35.445901° 122.997344° 35.445901 122.997344 度分 35°26.7541′ 122°59.8406′ 3526.7541 12259.8406 度分秒 35°26′45.245″ 122°59′50.438″ 352645.245 1225950.438
(6)正投影按选定格式在“输入”栏输入经纬度值,反投影输入以米为单位的X、Y坐标值。
(7)单击“单点转换”按钮。
(8)在“输出”栏查看计算结果。
批量转换步骤如下:
(1)准备好需要转换的输入数据文件,要求是文本文件,分两列,第一列纬度值或纵向坐标值,第二列经度值或横向坐标值,两列之间用空格分开。正向投影时,纬度值及经度值格式可以有三种选择,缺省当作十进制度处理;反向投影时,纵向及横向坐标值必须以米为单位。
下例为度分秒格式(WGS84)的6°带正投影输入数据文件 testdata.txt
352645.245 1225950.438 353800.402 1230000.378 351600.519 1225959.506 345800.101 1225959.8 343600.336 1230000.26 341400.018 1225959.897 335159.17 1225959.46 333000.08 1230000.28
(2)选择是高斯正转换还是反转换,缺省为经纬度转换到高斯投影坐标,投影坐标单位为米。
(3)选择大地基准面,缺省北京54,如果是GPS定位数据别忘了切换为WGS84。
(4)选择分带,3度或6度, 缺省为6度。
(5)输入中央经度,20带(114°E~120°E)中央经度为117度,21带(120°E~126°E)中央经度为123度。
(6)如正向投影,选择输入数据文件中的经纬度输入数据格式,有三个选项,缺省为十进制度格式。
(7)单击“批量转换”按钮。弹出打开文件对话框,输入你的数据文件名。
(8)输入转换结果文件名,单击“保存”后,程序开始进行计算。
(9)打开输出文件查看计算结果,结果分五列,第一序号,第二列输入纬度值或纵向坐标值,第三列输入经度值或横向坐标值,第四列转换后纬度值或纵向坐标值,第五列转换后经度值或横向坐标值。
下例为度分秒格式(WGS84)的6°带正投影转换结果数据文件 result.txt
1 352645.245 1225950.438 3924063.3 21499758.9 2 353800.402 1230000.378 3944871.4 21500009.5 3 351600.519 1225959.506 3904193.8 21499987.5 4 345800.101 1225959.8 3870898.1 21499994.9 5 343600.336 1230000.26 3830228.5 21500006.6 6 341400.018 1225959.897 3789544.4 21499997.4 7 335159.17 1225959.46 3748846.4 21499986.1 8 333000.08 1230000.28 3708205 21500007.2
三、分带方法:
(1)我国采用6度分带和3度分带:
1∶2.5万及1∶5万的地形图采用6度分带投影,即经差为6度,从零度子午线开始,自西向东每个经差6度为一投影带,全球共分60个带,用1,2,3,4,5,……表示.即东经0~6度为第一带,其中央经线的经度为东经3度,东经6~12度为第二带,其中央经线的经度为9度。
1∶1万的地形图采用3度分带,从东经1.5度的经线开始,每隔3度为一带,用1,2,3,……表示,全球共划分120个投影带,即东经1.5~ 4.5度为第1带,其中央经线的经度为东经3度,东经4.5~7.5度为第2带,其中央经线的经度为东经6度.我省位于东经113度-东经120度之间,跨第38、39、40共计3个带,其中东经115.5度以西为第38带,其中央经线为东经114度;东经115.5~118.5度为39带,其中央经线为东经117度;东经118.5度以东到山海关为40带,其中央经线为东经120度。地形图上公里网横坐标前2位就是带号,例如:1∶5万地形图上的横坐标为20345486,其中20即为带号,345486为横坐标值。2.当地中央经线经度的计算六度带中央经线经度的计算:当地中央经线经度=6°×当地带号-3°,例如:地形图上的横坐标为20345,其所处的六度带的中央经线经度为:6°×20-3°=117°(适用于1∶2.5万和1∶5万地形图)。三度带中央经线经度的计算:中央经线经度=3°×当地带号(适用于1∶1万地形图)。
(2)带号和中央经线的计算公式
3°带:
中央经线Lo=3*N
带号N=Lo/3