机器学习第七周--二分类算法逻辑回归

一.Logistic分类算法

     逻辑回归(Logistic Regression, LR)是传统机器学习中的一种分类模型，由于算法的简单和高效，解释性好以及容易扩展等优点，被广泛应用于点击率预估（CTR）、计算广告（CA）以及推荐系统（RS）等任务中。逻辑回归虽然名字叫做回归，但实际上却是一种分类学习方法。主要用于两分类问题，利用Logistic函数（或称为Sigmoid函数），自变量取值范围为(-INF, INF)，自变量的取值范围为(0,1)，函数形式为：

    由于sigmoid函数的定义域是(-INF, +INF),而值域为(0, 1)。因此最基本的LR分类器适合于对两分类（类0，类1）目标进行分类。Sigmoid 函数是个很漂亮的“S”形，如下图所示：

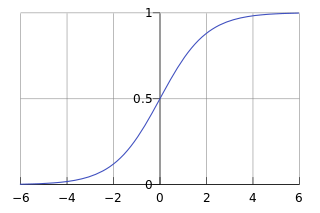
    LR分类器目的就是从训练数据特征学习出一个0/1分类模型，这个模型以样本特征的线性组合作为自变量，使用logistic函数将自变量映射到(0,1)上。因此LR分类器的求解就是求解一组权值（^Θ₀是是名义变量--dummy，为常数，实际工程中常另x0=1.0。不管常数项有没有意义，最好保留），并代入Logistic函数构造出一个预测函数：

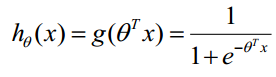
       函数的值表示结果为1的概率，就是特征属于y=1的概率。因此对于输入x分类结果为类别1和类别0的概率分别为：

       当我们要判别一个新来的特征属于哪个类时，按照下式求出一个z值： ，（x1,x2,...,xn是某样本数据的各个特征，维度为n）。进而求出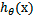---若大于0.5就是y=1的类，反之属于y=0类。（注意：这里依然假设统计样本是均匀分布的，所以设阈值为0.5）。LR分类器的这一组权值如何求得的呢？这就需要涉及到极大似然估计MLE和优化算法的概念了，数学中最优化算法常用的就是梯度上升（下降）算法。Logistic回归可以也可以用于多分类的，但是二分类的更为常用也更容易解释。所以实际中最常用的就是二分类的Logistic回归。LR分类器适用数据类型：数值型和标称型数据。其优点是计算代价不高，易于理解和实现；其缺点是容易欠拟合，分类精度可能不高。

二、梯度下降求解损失函数

   逻辑回归的损失函数是根据逻辑回归本身式子中系数的最大似然估计推导而来的，最大似然估计就是通过已知结果去反推最大概率导致该结果的参数。极大似然估计是概率论在统计学中的应用，它提供了一种给定观察数据来评估模型参数的方法，即 “模型已定，参数未知”，通过若干次试验，观察其结果，利用实验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。逻辑回归是一种监督式学习，是有训练标签的，就是有已知结果的，从这个已知结果入手，去推导能获得最大概率的结果参数，只要我们得出了这个参数，那我们的模型就自然可以很准确的预测未知的数据了。

令逻辑回归的模型为，则可以将其视为类1的后验概率，所以有：

                                 

  以上两个式子，可以改写为一般形式：

 

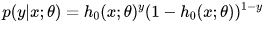
 因此根据最大似然估计，可以得到：

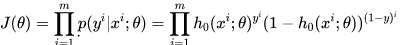
  为了简化计算，取对数将得到：

  我们希望极大似然越大越好，就是说，对于给定样本数量m，希望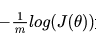越小越好，得到逻辑回归的损失函数如下：

 接下来需要找到一组参数，使得上面的损失函数达到最小值。这个损失函数是没有标准方程解的，因此在实际的优化中，我们往往直接使用梯度下降法来不断逼近最优解。

使用梯度下降法，就要求出梯度，对每一个向量中每一个参数，都求出对应的导数：

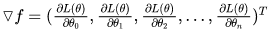
对sigmoid函数进行求导（链式求导法则）：

 然后对外层的log函数进行求导：

 然后进行整理：

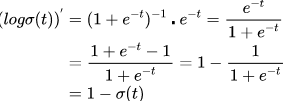
下面就可以对损失函数前半部分的表达式 对Θ进行求导了。带入上面的结果，得到：

 同样地，可以对损失函数的后半部分做求导，跟上面类似。最终求的损失函数L(Θ)对Θ的导数如下，即逻辑回归的损失函数经过梯度下降法对一个参数进行求导，得到结果如下：

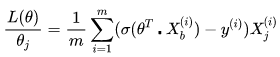
其中就是逻辑回归模型的预测值。

在求得对一个参数的导数之后，则可以对所有特征维度上对损失函数进行求导，得到向量化后的结果如下：

三.Python代码实现

import sklearn
from sklearn.linear_model import LogisticRegression as LR
sklearn.linear_model.LogisticRegression(penalty='l2',dual=False,tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1,   
    class_weight=None, random_state=None, solver='warn',max_iter=100, multi_class='warn', verbose=0,warm_start=False, n_jobs=None)

参数解释如下：

• penalty：惩罚项
  • str类型，默认为l2。newton-cg、sag和lbfgs求解算法只支持L2规范,L2假设的模型参数满足高斯分布。
  • l1:L1G规范假设的是模型的参数满足拉普拉斯分布.
• dual：对偶或原始方法，bool类型，默认为False。对偶方法只用在求解线性多核(liblinear)的L2惩罚项上。当样本数量>样本特征的时候，dual通常设置为False。
• tol：停止求解的标准，float类型，默认为1e-4。就是求解到多少的时候，停止，认为已经求出最优解。
• c：正则化系数λ的倒数，float类型，默认为1.0。必须是正浮点型数。像SVM一样，越小的数值表示越强的正则化。
• fit_intercept：是否存在截距或偏差，bool类型，默认为True。
• intercept _ scaling：仅在正则化项为”liblinear”，且fit_intercept设置为True时有用。float类型，默认为1。
• class_ weight：用于标示分类模型中各种类型的权重，可以是一个字典或者’balanced’字符串，默认为不输入，也就是不考虑权重，即为None。
  • 如果选择输入的话，可以选择balanced让类库自己计算类型权重，或者自己输入各个类型的权重。
  • 举个例子，比如对于0,1的二元模型，我们可以定义class_ weight = {0:0.9,1:0.1}，这样类型0的权重为90%，而类型1的权重为10%。如果class_ weight选择balanced，那么类库会根据训练样本量来计算权重。
  • 某种类型样本量越多，则权重越低，样本量越少，则权重越高。
  • 当class_ weight为balanced时，类权重计算方法如下：n_samples / (n_classes * np.bincount(y))。n_samples为样本数，n_classes为类别数量，np.bincount(y)会输出每个类的样本数，例如y=[1,0,0,1,1],则np.bincount(y)=[2,3]。
  • 其实这个数据平衡的问题我们有专门的解决办法：重采样
• random_state：随机数种子，int类型，可选参数，默认为无，仅在正则化优化算法为sag,liblinear时有用。
• solver：优化算法选择参数
  • liblinear：使用了开源的liblinear库实现，内部使用了坐标轴下降法来迭代优化损失函数。
  • lbfgs：拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
  • newton-cg：也是牛顿法家族的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。只用于L2
  • sag：即随机平均梯度下降，是梯度下降法的变种，和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度，适合于样本数据多的时候。只用于L2
  • saga：线性收敛的随机优化算法的的变重。只用于L2
• max_iter：算法收敛最大迭代次数，int类型，默认为10。仅在正则化优化算法为newton-cg, sag和lbfgs才有用，算法收敛的最大迭代次数。
• multi_class：分类方式选择参数，str类型，可选参数为ovr和multinomial，默认为ovr。ovr即前面提到的one-vs-rest(OvR)，而multinomial即前面提到的many-vs-many(MvM)。如果是二元逻辑回归，ovr和multinomial并没有任何区别，区别主要在多元逻辑回归上。
• verbose：日志冗长度，int类型。默认为0。就是不输出训练过程，1的时候偶尔输出结果，大于1，对于每个子模型都输出。
• warm_start：热启动参数，bool类型。默认为False。如果为True，则下一次训练是以追加树的形式进行（重新使用上一次的调用作为初始化）。
• n_jobs：并行数。int类型，默认为1。为-1的时候，用所有CPU的内核运行程序。

from sklearn import datasets
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

iris = datasets.load_iris()
X = iris.data
y = iris.target
X = X[y<2,:2]
y = y[y<2]
x_train,x_test,y_train,y_test = train_test_split(X,y,test_size=0.3,train_size=0.7,random_state=0)
sc = StandardScaler()
sc.fit(x_train)  # 计算均值和方差
x_train_std = sc.transform(x_train) #利用计算好的方差和均值进行Z分数标准化
x_test_std = sc.transform(x_test)

lr = LR(C=1000,random_state=123)
lr.fit(x_train_std,y_train)

y_pred = lr.predict(x_test_std)
lr.score(x_test_std,y_test) # 输出一个正确率
from sklearn.metrics import confusion_matrix,accuracy_score as AC
print(u"混淆矩阵",confusion_matrix(y_true=y_test,y_pred=y_pred))
print("正确率：",AC(y_test,y_pred))

　　以上是第七周的学习内容，留作参考。