1、满二叉树
除叶子结点外的所有结点均有两个子结点的二叉树称为满二叉树。如果一个满二叉树的深度为h,则结点个数为2^h - 1。
由满二叉树可推出,二叉树的第k层最多有2^(k-1)个结点,深度为h的二叉树最多有2^h-1个结点。如下图所示:
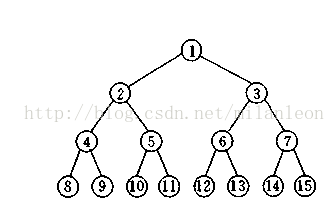
2、树的遍历
前序遍历:对结点的处理工作是在所有儿子结点之前。如下面对于文件系统树输出各文件的名字的算法:

void FileSystem::listAll()
{
printName();
if (isDirectory())
{
(for each child)
{
child.listAll();
}
}
}
后序遍历:对结点的处理工作是在所有儿子结点处理之后进行。如下面对于文件系统树获得其大小的算法:

void FileSystem::size()
{
int totalSize = sizeOfThisFile();
if (isDirectory())
{
(for each child)
{
totalSize += child.size();
}
}
return totalSize;
}
3、set和map
平衡二叉树:左右两个子树的高度差不超过1,并且左右两个子树也满足上述规则,即也是一个平衡二叉树。
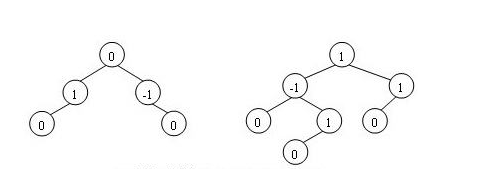
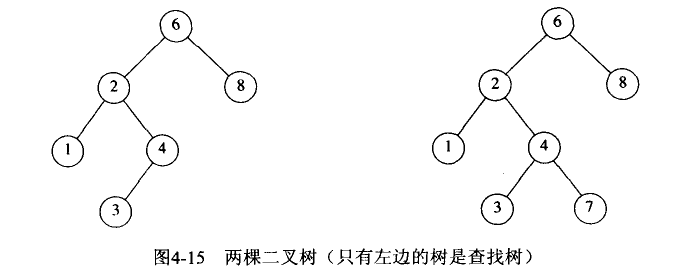
二叉查找树:又称二叉排序树,对于每个树节点来说,其左子树上的值都小于该节点树的值,其右子树上的值都大于该节点树的值。二叉查找树的左右高度差无任何限制,这样在最坏的情况下变成了一个链式存储线性表,其查询时间复杂度线性增长为O(n)。

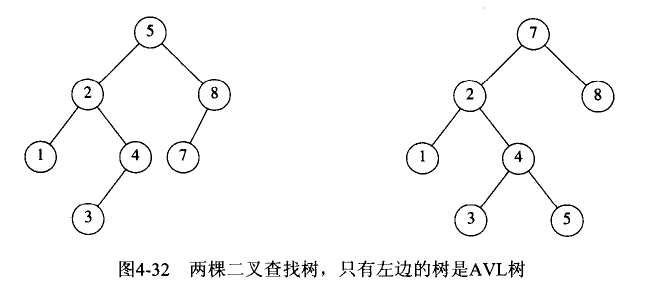
平衡二叉查找树:二叉查找树 +平衡二叉树,AVL树是最早的平衡二叉查找树,它的左右高度差可以保证在[-1, 0, 1],查询的时间复杂度为O(logn)。当向AVL树插入元素的时候需要遵循一定的插入方法或者规则来保证结果还是一个AVL树,这些插入方法或者规则被形象的称为“旋转”。因为维护AVL树的代价比较高,所以它只适合应用于插入、删除不频繁的场景。
红黑树(R-B树):红黑树也被认为属于平衡二叉查找树,虽然它的左右高度差可能超过1,但最坏的情况是从根到叶子的最长路是最短路的两倍,不算太差,其查询的时间复杂度也为O(logn)。红黑树如下图,它具有以下特征: ①、结点是红色或黑色,根结点是黑色。
②、叶子结点都是黑色的空节点(NIL)。
③、红色结点的两个子结点都是黑色的。
④、从任一结点到每个叶子结点的所有简单路径都包含相同数目的黑色结点。
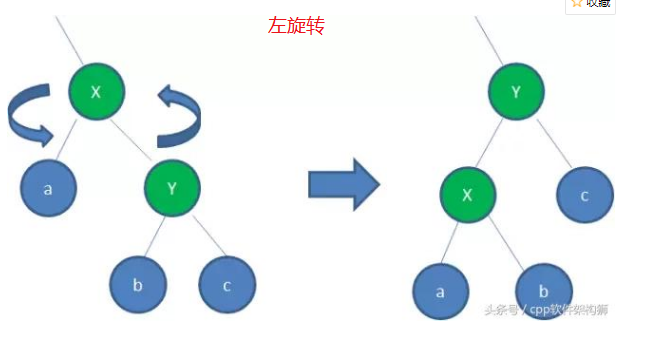
与AVL树类似,当向红黑树插入或删除结点的时候可能会把上述的规则特征破坏,所以就需要进行调整来使插入后保持红黑树的规则,调整的方式有“变色”和“旋转”,其中旋转又有“左旋”和“右旋”两种方式,“左旋”是逆时针旋转两个结点,使父结点被自己的右孩子取代,而自己成为左孩子。
红黑树的应用有C++的map和set。

B/B+ Tree:B树和B+树的特点是每个结点可以有超过两个的子结点,相当于是一个N叉平衡树。使用示例为磁盘文件组织和数据库索引。
vector、list、deque查找时效率都很低,set和map提供了高效的查找、插入和删除操作,在最坏的情况下查找、插入和删除仅消耗log(n)对数时间,因为set和map实现基于自顶向下红黑树,对于100万条记录,最多也只要20次的比较就可以查找到。
4、priority_queue
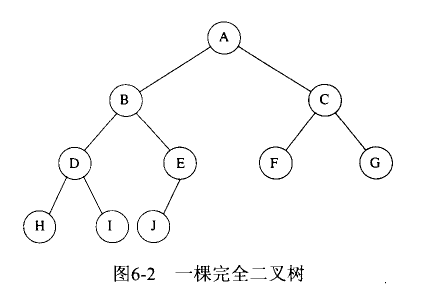
二叉堆:又称为完全二叉树,如果一个二叉树的深度为h,那么除了h层外,其它各层的结点数都达到最大值,且第h层的所有结点都连续集中在最左边的二叉树,如下图:
优先队列是可以设置元素的优先级的数据结构,它一般使用二叉堆来实现。c++中优先队列的实现是priority_queue,它要求提供随机访问的功能,所以其所关联的基础容器可以为vector、deque,默认基础容器为vector。
