昨天就得到消息今天会考达哥冥思苦想出来的一套题,不胜惶恐以致过于紧张到只能颓游记
今天早上又一直没有睡醒,整个早读时间好像真的什么也没有干(除了死记硬背过的手写堆)
考试时候先瞟了一眼第一题,期望dp滚粗感强烈,直接看下一题
第二题怎么看都是n^3,去了趟周测然而并没有什么思路,看第三题
第三题上来,诶问题一怎么和上一次某题一模一样,问题二打了个表开始对组合数,成功yy出规律(考完才发现这tm就是卡特兰数,我竟然没看出来)
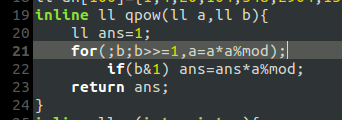
然后想着先码出来部分分,然后我就死了,调了一个小时才发现mdzz快速幂打错了,这里直接上图


吃了一口shit之后去看问题三,并没有什么想法然后去看问题四,发现诶这不问题一+问题二吗(还没看出来卡特兰),码完继续yy第三问规律,无果
最后第三问暴力打表骗到了5分,加上其他几问一共80
然后去yyT2,成功找出opt==0的算法,yy,opt==1的正解无果,高斯消元硬干还忘了四舍五入,导致opt==1只得了10分,加上opt==0一共40
最后还剩20min去yyT1,无果打了个n^m算法,先交了个TLE 0pts,后来想着加个clock忘记了函数调用顺序,成功得到了蓝蓝的ce,鼓掌
最终得分0+40+80=120,rank10,看来昨天给我妈打电话真是个惊天flag
T1:随
hz惯例,最难T1,这次直接放了之前完全不会的一些东西上去,以下需要用到这些知识:矩阵快速幂,循环矩阵,原根
首先对于前两个测试点,直接特判就能得,不再赘述,期望得分20
对于3~5的测试点,设dp[i][j]表示i次操作后值为j的概率,直接转移是O(m*mod^2),用矩阵快速幂可以变成O(mod^3*logm),没有太大区别,都能得到50pts
对于后面的点,这里引入一个东西——原根
不过这里只需要用到原根的一些性质,即对于n的原根rt,rt^k能取遍(1,n-1)的所有值
利用这个性质,我们可以把本来没有规律的乘法转移矩阵变成有规律的加法转移矩阵,那么利用循环矩阵我们可以把n^3的矩阵乘变成n^2的循环矩阵乘
复杂度O(n^2logm)

1 #include<bits/stdc++.h>
2 #define ll long long
3 const int MOD=1e9+7;
4 using namespace std;
5 int mod,n,m,t[100010],top,jie[1010];long long aa[1010],ans[1010],now[1010];
6 bool v[1010];
7 void mul(){
8 for(int j=0;j<mod;j++){
9 now[j]=0;
10 for(int k=0;k<mod;k++) (now[j]+=aa[k]*aa[(j-k+mod-1)%(mod-1)])%=MOD;
11 }
12 for(int i=0;i<mod-1;i++) aa[i]=now[i];
13 }
14 void muls(){
15 for(int j=0;j<mod-1;j++){
16 now[j]=0;
17 for(int k=0;k<mod-1;k++) (now[j]+=ans[k]*aa[(j-k+mod-1)%(mod-1)])%=MOD;
18 }
19 for(int i=0;i<mod-1;i++) ans[i]=now[i];
20 }
21 inline int qpow(int a,int b){
22 int ans=1;
23 for(;b;b>>=1,a=1ll*a*a%MOD)
24 if(b&1) ans=1ll*ans*a%MOD;
25 return ans;
26 }
27 int main(){
28 int x,opt,rt;
29 scanf("%d%d%d",&n,&m,&mod);
30 for(int i=1;i<mod;i++){
31 memset(v,0,sizeof v);opt=1;
32 for(int j=i,k=1;k<mod;k++,j=j*i%mod)
33 if(v[j]) {
34 opt=0;
35 break;
36 }
37 else v[j]=1;
38 if(opt){
39 rt=i;
40 break;
41 }
42 }
43 jie[0]=1;
44 for(int i=1;i<=mod-1;i++) jie[i]=jie[i-1]*rt%mod;
45 for(int i=1;i<=n;i++){
46 scanf("%d",&x);
47 t[x]++;
48 }
49 for(int j=0;j<mod-1;j++)
50 aa[j]+=t[jie[j]];
51 top=m;
52 ans[0]=1;
53 for(;m;m>>=1,mul())
54 if(m&1) muls();
55 long long ens=0;
56 for(int i=0;i<mod-1;i++) ens+=jie[i]*ans[i];
57 ens%=MOD;
58 ens=ens*qpow(qpow(n,top),MOD-2)%MOD;
59 printf("%d",(int)ens);
60 }
T2:单
最近成天做树上dp,然而并不能想到正解,只能打打60pts暴力(还打错只得了40pts)才能维持的了生活这样子
对于给a求b的询问,我们可以暴力求出节点1的b值,然后考虑从父亲向儿子转移,设sum[i]表示以i为根的字树a值合,则有
b[son]=b[fa]+(sum[1]-sum[son])(子树以外的点到儿子距离增加1)-sum[son](子树上的点到儿子距离减少1),拿到opt==0的30pts
然后考虑opt==1的询问,将上面式子移项即可得到
b[son]-b[fa]=sum[1]-2*sum[son] (1)
同时b[1]=∑sum[i](2<=i<=n) (2)
我们发现如果把所有的(1)式求和再和(2)式做差,就可以消掉sum[1]外所有的sum[i],就可以得到sum[1],再dfs一遍进行回代,就可以得出每个点的a值
总复杂度O(T*n)

1 #include<bits/stdc++.h>
2 using namespace std;
3 long long a[100010],b[100010],sum;
4 int fa[100010],to[200010],la[200010],num,sz[100010],n;
5 inline void add(const int x,const int y){
6 to[++num]=y;
7 la[num]=fa[x];
8 fa[x]=num;
9 }
10 void dfs1(int x,int ff,int len){
11 b[1]+=a[x]*len;
12 sz[x]=a[x];
13 for(int i=fa[x],y=to[i];i;i=la[i],y=to[i])
14 if(y!=ff){
15 dfs1(y,x,len+1);
16 sz[x]+=sz[y];
17 }
18 }
19 void dfs2(int x,int ff){
20 if(x!=1) b[x]=b[ff]+sum-sz[x]-sz[x];
21 for(int i=fa[x];i;i=la[i])
22 if(to[i]!=ff) dfs2(to[i],x);
23 }
24 void dfs3(int x,int ff){
25 for(int i=fa[x];i;i=la[i])
26 if(to[i]!=ff){
27 dfs3(to[i],x);
28 sz[x]+=sz[to[i]];
29 }
30 if(x!=1) a[x]=(b[ff]-b[x]-2*sz[x]+sum)>>1,sz[x]+=a[x];
31 }
32 inline void dfss(int x,int ff){
33 if(x!=1) sum+=b[ff]-b[x];
34 for(int i=fa[x];i;i=la[i])
35 if(to[i]!=ff) dfss(to[i],x);
36 }
37 signed main(){
38 int x,y,opt,T;
39 scanf("%d",&T);
40 while(T--){
41 memset(a,0,sizeof a);
42 memset(b,0,sizeof b);
43 memset(fa,0,sizeof fa);
44 memset(sz,0,sizeof sz);
45 scanf("%lld",&n);num=0;
46 for(int i=2;i<=n;i++){
47 scanf("%d%d",&x,&y);
48 add(x,y);add(y,x);
49 }
50 scanf("%d",&opt);
51 if(!opt){
52 sum=0;
53 for(int i=1;i<=n;i++) scanf("%lld",&a[i]),sum+=a[i];
54 dfs1(1,0,0);
55 dfs2(1,0);
56 for(int i=1;i<=n;i++) printf("%lld ",b[i]);
57 puts("");
58 }
59 else {
60 //memset(aa,0,sizeof aa);
61 for(int i=1;i<=n;i++) scanf("%lld",&b[i]);
62 sum=0;
63 dfss(1,0);
64 sum=(2*b[1]-sum)/(n-1);
65 dfs3(1,0);a[1]=sum;
66 for(int i=2;i<=n;i++) a[1]-=a[i];
67 for(int i=1;i<=n;i++) printf("%lld ",a[i]);
68 puts("");
69 }
70 }
71 }
T3:题
再次T3最水,还好没有先做T1T2
其实没什么好说的,Q1上次原题,Q2卡特兰数,Q3直接dp,Q4=Q1+Q2

1 #include<bits/stdc++.h>
2 using namespace std;
3 #define ll long long
4 const int mod=1e9+7;
5 ll jie[100010],ni[100010],ans=0,f[2][2010][2010];
6 inline ll qpow(ll a,ll b){
7 ll ans=1;
8 for(;b;b>>=1,a=a*a%mod)
9 if(b&1) ans=ans*a%mod;
10 return ans;
11 }
12 inline ll c(int x,int y){
13 if(!y) return 1;
14 return jie[x]*ni[y]%mod*ni[x-y]%mod;
15 }
16 int main(){
17 int n,m;
18 scanf("%d%d",&n,&m);
19 jie[1]=1;jie[0]=1;
20 for(int i=2;i<=n;i++) jie[i]=jie[i-1]*i%mod;
21 ni[n]=qpow(jie[n],mod-2);
22 for(int i=n;i>=1;i--) ni[i-1]=ni[i]*i%mod;
23 switch(m){
24 case 0:{
25 for(int i=0;i<=n/2;i++)
26 ans=(ans+c(n,i)*c(n-i,i)%mod*c(n-i*2,(n-i*2)/2)%mod)%mod;
27 printf("%lld",ans);
28 return 0;
29 }
30 case 1:{
31 ans=c(n,n/2)*qpow((n/2)+1,mod-2)%mod;
32 printf("%lld",ans);
33 return 0;
34 }
35 case 3:{
36 for(int i=0;i<=n/2;i++)
37 ans=(ans+c(n,i)*c(n-i,i)%mod*c((n-i*2),(n-i*2)>>1)%mod*qpow(i+1,mod-2)%mod*qpow((n-i*2)/2+1,mod-2)%mod)%mod;
38 printf("%lld",ans);
39 return 0;
40 }
41 case 2:{
42 memset(f,0,sizeof f);
43 int now=1;
44 f[now][n][n]=1;
45 for(int i=1;i<=n;i++){
46 now^=1;
47 for(int j=-n/2;j<=n/2;j++){
48 if(j) f[now][j+n][n]=(f[now^1][j-1+n][n]+f[now^1][j+1+n][n])%mod;
49 }
50 for(int j=-n/2;j<=n/2;j++){
51 if(j) f[now][n][j+n]=(f[now^1][n][j+1+n]+f[now^1][n][j-1+n])%mod;
52 }
53 f[now][n][n]=(f[now^1][n][1+n]+f[now^1][n][n-1]+f[now^1][n+1][n]+f[now^1][n-1][n])%mod;
54 }
55 printf("%lld",f[now][n][n]);
56 return 0;
57 }
58 }
59 }
我待曙色沾霜,才知南柯一场
