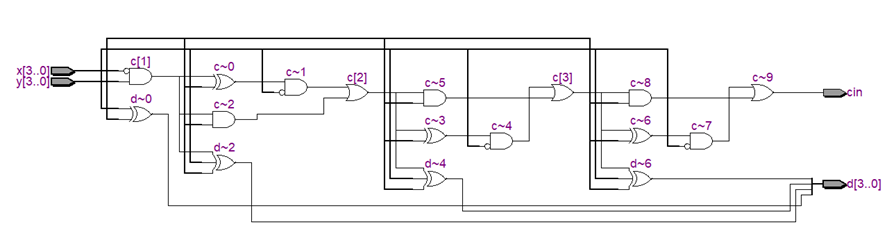
类似于行波进位加法器,用串联的方法也能够实现多位二进制数的减法操作。 比如下图是4位二进制减法逻辑电路图。
8位二进制减法的verilog代码如下:
module subn(x, y, d,cin); parameter n=8; input [n-1:0] x; input [n-1:0] y; output reg[n-1:0] d; //diff output reg cin; //borrow from high bit reg [n:0] c; integer k; always @(x,y) begin c[0] = 1'b0; for(k = 0; k < n; k = k + 1) begin d[k] = x[k]^y[k]^c[k]; c[k+1] = (~x[k]&(y[k]^c[k]))|(y[k]&c[k]); end cin = c[n]; end endmodule
module subn( x, y, d,cin);
parameter n=8;
input [n-1:0] x;
input [n-1:0] y;
output [n-1:0] d;
output cin;
assign {cin, d} = x - y ;
endmodulemodule subn( x, y, d,cin);
parameter n=8;
input [n-1:0] x;
input [n-1:0] y;
output [n-1:0] d;
output cin;
wire [n:0] c;
genvar k;
assign c[0]=0;
assign cin=c[n];
generate
for(k = 0; k <= n-1; k = k + 1) begin:subbit
fullsub stage(c[k],x[k],y[k],d[k],c[k+1]);
end
endgenerate
endmoduletestbench 代码如下:
`timescale 1ns/1ns
`define clock_period 20
module subn_tb;
reg [7:0] x,y;
wire cin;
wire [7:0] d;
reg clk;
subn #(.n(8)) subn_0(
.x(x),
.y(y),
.d(d),
.cin(cin)
);
initial clk = 0;
always #(`clock_period/2) clk = ~clk;
initial begin
x = 0;
repeat(20)
#(`clock_period) x = $random;
end
initial begin
y = 0;
repeat(20)
#(`clock_period) y = $random;
end
initial begin
#(`clock_period*20)
$stop;
end
endmodule功能验证的波形图如下。注意:我们选择了radix为unsigned