2进制，10进制，16进制，补码和移位

逢二进一，逢十进一，十六进制

10110101(2)  = 128+32+16+4+1 = 181(10)
   b   5(16) = b*16+5 = 11*16+5 = 181(10) 

2进制

int n = 45;
System.out.println(Integer.toBinaryString(n));

计算机的内部(Java)只有2进制数据, 在显示的时候编程语言提供API将2进制转换为10进制显示出来.

计算机只能处理2进制数据, 利用编程语言提供的算法支持了10进制

Java中用于支持2进制两个算法(方法):

1. Integer.toString() 将内存2进制数据转换为10进制输出

2. Integer.parseInt() 将10进制字符串转换为2进制数据

   int n = Integer.parseInt("22271"); System.out.println(Integer.toString(n));//"22271"

计算机"表面上"支持了10进制

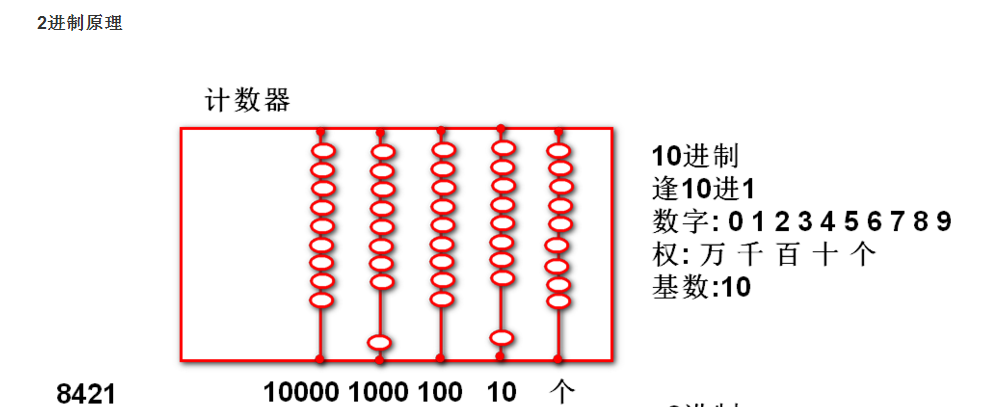
2进制的计数原理

逢2进1的计数规则.

2进制原理

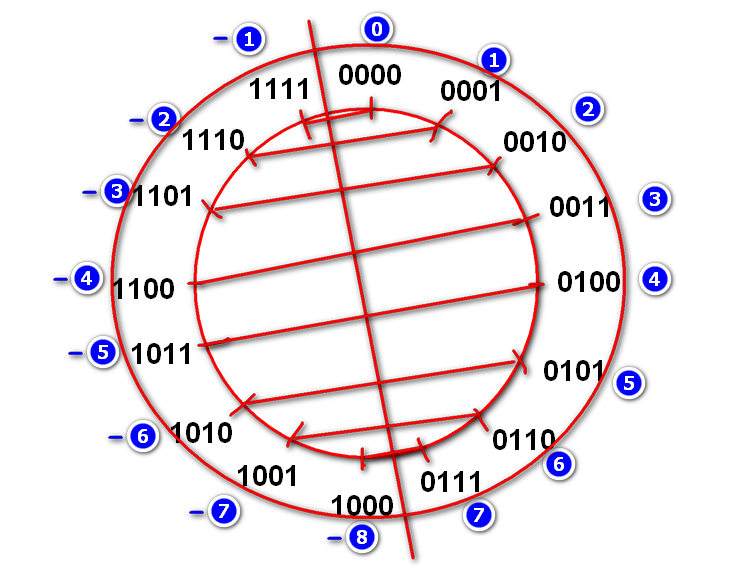
4位数2进制全排列

如:

8421
0000   0
0001   1
0010   2
0011   3
0100   4
0101   5
0110   6
0111   7
1000   8
1001   9
1010  10
1011  11
1100  12
1101  13
1110  14
1111  15 

Java 验证代码:

for(int i=0; i<16; i++){
    System.out.println(Integer.toBinaryString(i));
}

如何将2进制转换为10进制

将2进制每个数字代表的1的个数进行求和即可:

10111101(2)
=32+16+8+4+1(10)
=128+32+29             
=128+61
=189(10)

Java 代码验证:

System.out.println(Integer.toBinaryString(189));

案例, 将2进制转换为10进制:

 11010101(2)       10011011(2) 
=?(10)            =?(10)

 10101101(2)       11101101(2)
=?(10)            =?(10)

案例: 10进制转换为2进制

          128 64 32 16 8 4 2 1
183(10) =   1  0  1  1 0 1 1 1(2)
           55    23  7   3 1 0
        = 10110111(2)

234(10) = ?(2)
209(10) = ?(2)
200(10) = ?(2)
199(10) = ?(2)

为啥要用2进制

计算机采用2进制作为计算数据, 其成本最优!

使用2进制

16进制

用于简写2进制(缩写2进制), 原因是2进制的书写过于冗长, 2进制的每4位缩写为一个16进制数. 按照这个规则可以将2进制简写.

01011111 11011101 11011011 00010010 (2)
   5   f    d   d    d   b    1   2 (16)

16进制与2进制的对应关系

2进制 16进制    
0000   0
0001   1
0010   2
0011   3
0100   4
0101   5
0110   6
0111   7
1000   8
1001   9
1010   a
1011   b
1100   c
1101   d
1110   e
1111   f 

案例: 验证16进制与2进制的对应关系

10110101(2)  = 128+32+16+4+1 = 181(10)
   b   5(16) = b*16+5 = 11*16+5 = 181(10) 

验证:

int n = 0xb5;
System.out.println(Integer.toBinaryString(n)); 
System.out.println(n); 

编程时候凡是需要书写2进制数据时候, 都采用16进制作为缩写!!

补码

是一种利用"正数"表示"负数"的"算法", 节省了硬件成本!!!

4位数补码原理:

任何计算超过4位数自动溢出舍弃

0000    
0001    
0010    
0011    
0100    
0101    
0110    
0111    
1000    
1001    
1010    
1011    
1100    
1101    
1110    
1111
0000     
0001
0010
...

案例:

for(int i=-10; i<10; i++){
    System.out.print(Integer.toString(i)+" ");
    System.out.println(Integer.toBinaryString(i));
}

补码规律(int):

1. 0 是 32位0
2. -1 是 32位1
3. max 是 01111111 11111111 11111111 11111111
4. min 是 10000000 00000000 00000000 00000000

补码面试题:

System.out.println(Integer.MIN_VALUE-Integer.MAX_VALUE);
选择如上代码的运行结果:  
A. 2147483647 B.-2147483648 C.4294967296 D.1 E.-1

补码面试题:

System.out.println(Integer.MIN_VALUE-1);
选择如上代码的运行结果:  
A. 2147483647 B.-2147483648 C.4294967296 D.1 E.-1

补码面试题:

System.out.println(~88);
选择如上代码的运行结果:  
A. 88 B.-88 C.89 D.-89 E.98

2进制的运算符

~ 取反

>>> >> << 移位运算

& | 与 或 运算

>>> 逻辑右移位运算

运算规则: 将数字向右移动,高位补充0, 低位溢出舍弃

n = 01101101 00010001 11001001 10011011
m = n>>>1
m = 001101101 00010001 11001001 1001101
k = n>>>2
k = 0001101101 00010001 11001001 100110

验证:

int n = 0x6d11c99b;
int m = n>>>1;
int k = n>>>2;
//...
System.out.println(Integer.toBinaryString(n));
System.out.println(Integer.toBinaryString(m));
System.out.println(Integer.toBinaryString(k));

<< 逻辑右移位运算

运算规则: 将数字向左移动,低位补充0, 高位溢出舍弃

n = 01101101 00010001 11001001 10011011
m = n<<1
m = 1101101 00010001 11001001 100110110
k = n<<2
k = 101101 00010001 11001001 1001101100

验证: 略

移位运算的数学意义

引子:

移动小数点运算:

数据  33128. 右移动小数点一次
结果 331280. 原始数据乘以10

假设小数点不动,则数字向左移动,数字向左移动一次原始数据乘以基数(10)一次

2进制同样有效

举个栗子:

n = 00000000 00000000 00000000 01100100.  //100
m = n<<1;
m = 0000000 00000000 00000000 011001000.     //200
k = n<<2;
k = 400

验证:

int n = 100;
int m = n<<1;
int k = n<<2;
System.out.println(n);//100
System.out.println(m);//200
System.out.println(k);//400

>>> 与 >>

>>> 向右移动, 高位永远补0, 负数时候不符合数学除法规律 >> 数位向右移动, 高位为1(负数) 则补1, 高位为0(正数) 则补0, 保持符号位不变, 其结果符合数学除法规律(自动向小方向取整)

案例:

int n = -36;
int m = n>>1;//m = -18
int k = n>>>1; //? 不符合数学规律
System.out.println(Integer.toBinaryString(n));
System.out.println(Integer.toBinaryString(m));
System.out.println(Integer.toBinaryString(k));  

& 与运算

逻辑乘法

1 & 1 = 1
0 & 1 = 0
1 & 0 = 0
0 & 0 = 0

计算规则: 两个数上下对齐, 对应位数进行与计算

n = 01100011 00100110 00110111 11011110 
m = 00000000 00000000 00000000 11111111  mask
k = n&m;
k = 00000000 00000000 00000000 11011110

代码:

//掩码运算
int n = 0x632637de;
int m = 0xff;
int k = n&m;
System.out.println(Integer.toBinaryString(n));
System.out.println(Integer.toBinaryString(m));
System.out.println(Integer.toBinaryString(k));

经典用途: 截取一个数据的后8位, 称为"掩码(mask)"运算

移位运算的用途

与掩码运算配合, 将数据进行拆分:

//将int n 拆分为 4个 8位数 b1 b2 b3 b4 
int n = 0x632637de;
int m = 0xff;
int b1 = n&m;
int b2 = (n>>>8) & m;
int b3 = (n>>>16) & m;
int b4 = (n>>>24) & m;

| 或运算 : 将数据进行合并

规则类似 加法

1 | 1 = 1
0 | 1 = 1
1 | 0 = 1
0 | 0 = 0

上下对齐计算或

案例:

b1= 00000000 00000000 00000000 10011101
b2= 00000000 00000000 00000000 01101111
b3= 00000000 00000000 00000000 11101111
b4= 00000000 00000000 00000000 00110011

n = (b1<<24)|(b2<<16)|(b3<<8)|b4
    10011101 00000000 00000000 00000000 
    00000000 01101111 00000000 00000000 
    00000000 00000000 11101111 00000000 
    00000000 00000000 00000000 00110011

n=  10011101 01101111 11101111 00110011

或运算的经典用途

将字节数据合并为int数据:

代码: int b1 = 0x9d; int b2 = 0x6f; int b3 = 0xef; int b4 = 0x33; int n = (b1<<24)|(b2<<16)|(b3<<8)|b4; System.out.println(Integer.toBinaryString(b1)); System.out.println(Integer.toBinaryString(b2)); System.out.println(Integer.toBinaryString(b3)); System.out.println(Integer.toBinaryString(b4)); System.out.println(Integer.toBinaryString(n));