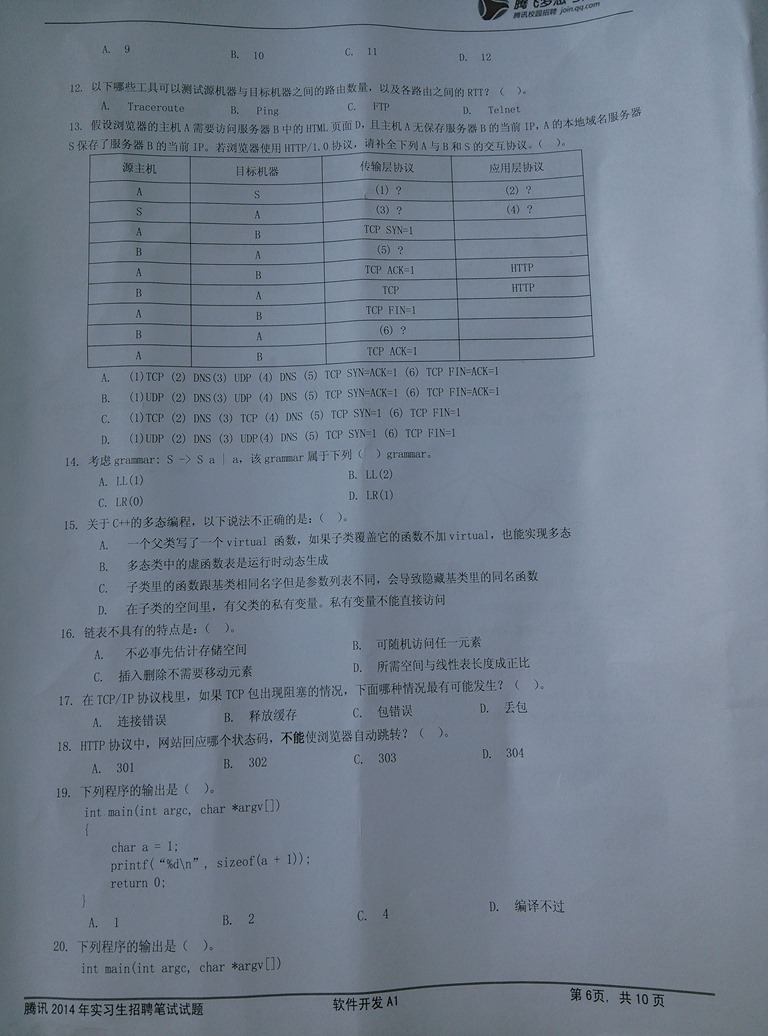
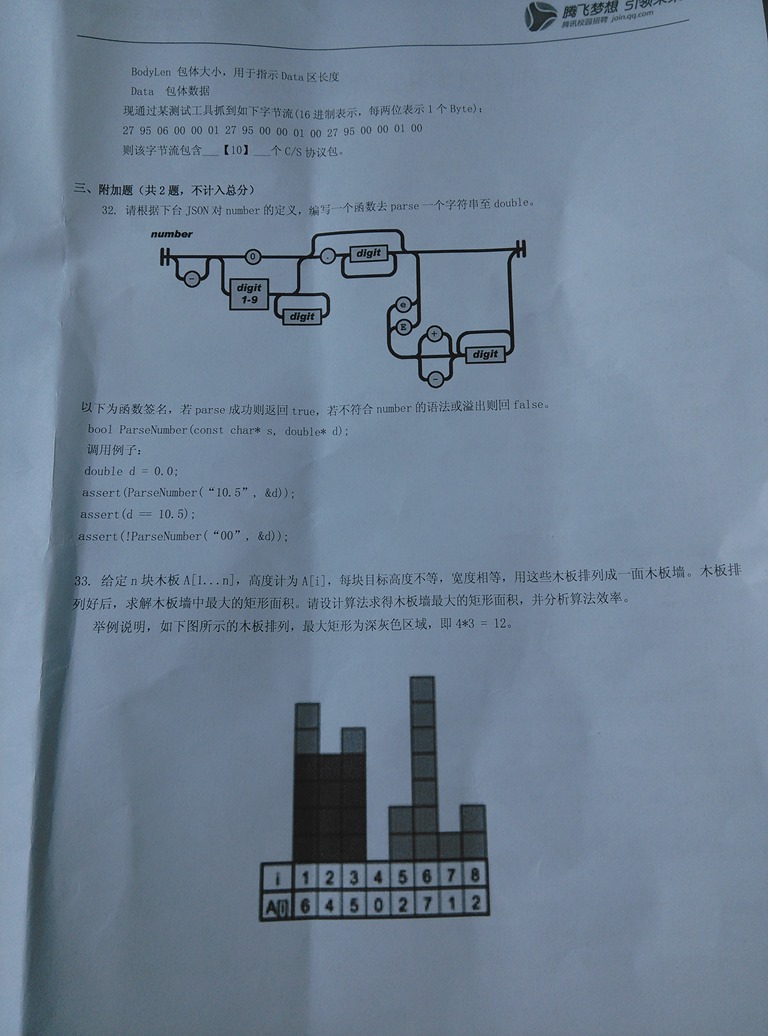
注:以上图片来自网络,非常感谢拍照者提供
附最后一提实现代码:
#include<iostream> #include<iterator> #include<stack> using namespace std; int MaxArea(int *arr, int len) { if(arr == NULL || len <= 0) return 0; stack<pair<int,int> > my_stack;//存放每个元素和其对应的长度 int top = 0,max = 0; int i = 0; while(i < len) { if(arr[i] > top) { my_stack.push(make_pair(arr[i],1));//第一次出现,将元素值(高度)和长度1压入栈中 } else { /* pre用来记录将要加入栈中元素对于的矩形长度,因为当前要处理的元素小于栈顶元素 表明当前元素长度可以向前延伸,有栈中有几个元素大于当前元素即表示当前元素 矩形长度可以延伸多少 */ int pre = 0; while(arr[i] < top){ /*小于栈顶元素,表明栈顶元素对应的矩形不可能再延伸了,即长度不会再加了 这时可以求出栈顶元素对应的矩形面积,在与保存的最大值比较,进行最大面积更新 */ int time = my_stack.top().second; pre += time; max = top*pre > max ? top*pre : max;//将栈顶元素对应的矩形面积与保存的最大值比较 my_stack.pop(); if(!my_stack.empty())//栈不为空,则当前元素继续与栈顶元素比较 top = my_stack.top().first; else break; } //循环退出时,如果栈不为空且栈顶元素等于当前元素,则进行矩形长度合并 if(!my_stack.empty() && my_stack.top().first == arr[i]) my_stack.top().second += pre+1;//+1表示将当前元素也计算在内 else{//否则,将当前元素入栈 my_stack.push(make_pair(arr[i],pre+1)); } } top = my_stack.top().first;//更新top保存的栈顶元素,准备与下一个取出的元素进行比较 ++i; } int pre = 0; /* 上面while退出后,栈中元素为递增 如数组为 {1,2,3,4,5,4}时,此时上面程序只是对5进行了矩形面积求值,然后栈中剩下单增元素{1,2,3,4} 现在从栈中逐个弹出,进行max求值 */ while(!my_stack.empty())//判断栈是否为空,不为空,则表示此时栈中都是递增的 { int time = my_stack.top().second; int top = my_stack.top().first; pre += time; max = top*pre > max ? top*pre : max;//将栈顶元素对应的矩形面积与保存的最大值比较 my_stack.pop(); } return max; } int main() { //int arr[] = {1,2,3,4,3,4,3,2,1}; int arr[] = {6,4,5,0,2,7,1,2}; //int arr[] = {1,2,3,4,5,4}; int len = sizeof(arr) / sizeof(int); int Max = MaxArea(arr,len); cout<<"max:"<<Max<<endl; return 0; }