数据分析-jupyter

安装 jupyter

pip install jupyter

快捷键  

　　插入 cell ： a  b

　　删除cell  :  x

　　切换cell的模式： m  y

　　执行  shift +enter

　　查看帮助文档： shit + tab

基础部分：

　　　　　　　使用首先导包

　　　　　　　　import numpy as np

　　　　　　　　import matplotlib.pyplot as plt

　　　　　　

一维数组创建
np.array([1,2,3,5,6])

二维数组创建

np.array([[1,2,3,],[4,5,6])

注意：

• numpy默认ndarray的所有元素的类型是相同的
• 如果传进来的列表中包含不同的类型，则统一为同一类型，优先级：str>float>int
• np.array([[1,'abc',3],[4,5,4]]) 

使用matplotlib.pyplot获取一个numpy数组，数据来源于一张图片

img_arr = plt.imread('./cat.jpg')   #导入图片

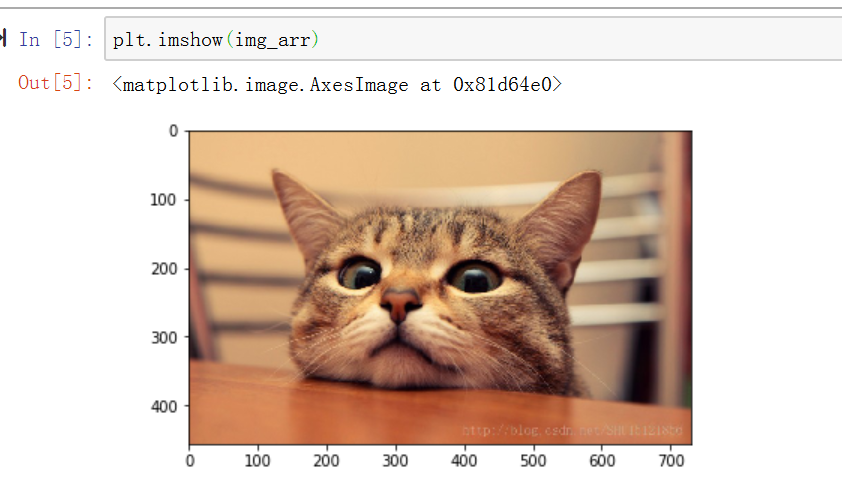
plt.imshow(img_arr)  #显示图片

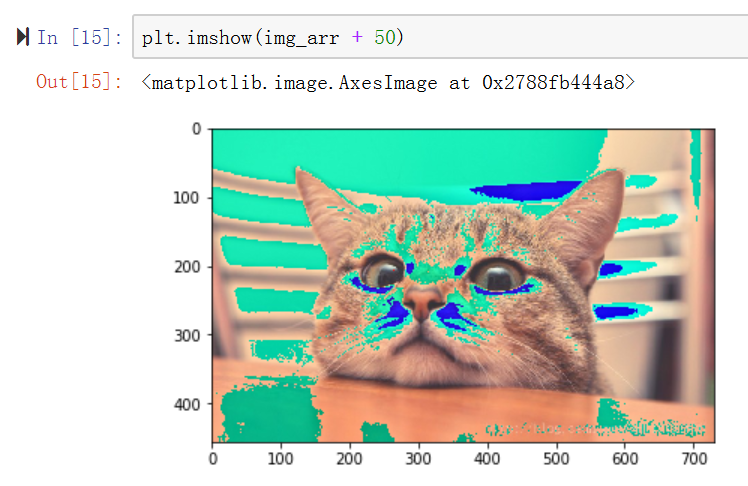
图片是一个三维的数组可以直接改变图片  例如  img_arr + 50

 

改变后的

img_arr.shape  #图片的前两位是像素，第三位是 颜色

 ##########################################################################

2. 使用np的routines函数创建

包含以下常见创建方法：

1) np.ones(shape, dtype=None, order='C')

img_arr.dtype #查看类型

np.ones((5,6)) #五行六列的数组

2) np.zeros(shape, dtype=None, order='C')

np.zeros((5,6)) #标书5行6列的数组 值是0

3) np.full(shape, fill_value, dtype=None, order='C')   #指定数值

5) np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None) 等差数列

np.linspace(0,100,num=50)   # 等差数列，创建一维的数组

6) np.arange([start, ]stop, [step, ]dtype=None)

np.arange(1,100,2)  #一维数组从1到100，步是2

7) np.random.randint(low, high=None, size=None, dtype='l')

np.random.randint(50,100,size=(7,9))  #创建随机数，实例50到100,7行9列

8) np.random.randn(d0, d1, ..., dn)

标准正太分布

　　np.random.randn(5,6)  #5行6列

9) np.random.random(size=None)

生成0到1的随机数，左闭右开 np.random.seed(3)

np.random.random(size=(3,4))

二、ndarray的属性

4个必记参数： ndim：维度 shape：形状（各维度的长度） size：总长度

dtype：元素类型

1. 　　arr[1] #索引获取的是第一行

切片

一维与列表完全一致 多维时同理

• 　　#获取二维数组前两行

　　　　　　arr[0:2]

• 　　#获取二维数组前两列。逗号左边的是行，右边的是列

　　　　　　arr[:,0:2]

• #获取前两行的前两列

　　　　　　arr[0:2,0:2]

将数据反转，例如[1,2,3]---->[3,2,1]

• #将数组的行倒叙

　　　　arr[::-1]

• #列倒序

　　　　arr[:,::-1]

• #全部倒序

　　　　arr[::-1,::-1]

图片:进行切片

　　　　#将图片进行全倒置操作
　　　　plt.imshow(img_arr)

　　　　　　plt.imshow(img_arr[:,::-1,:])  列倒序

　　　　　　plt.imshow(img_arr[::-1,:,:]) 行倒叙

　　　　　　plt.imshow(img_arr[::-1,::-1,::-1]) #这里行、列、颜色、都进行了倒序 

变形

原始数据  7行9列 7*9=63个数据

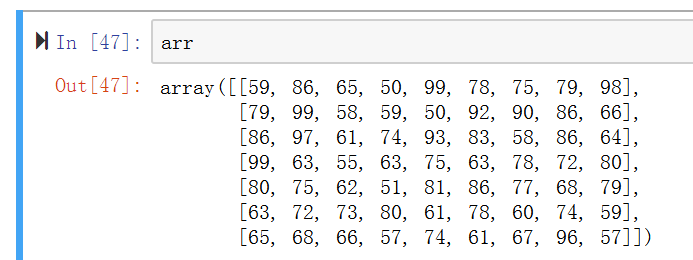
3. 变形¶

使用arr.reshape()函数，注意参数是一个tuple！

• 多维变一维必须是和原始数据的元素是一样的否则无法变形
• arr_1 =arr.reshape((63,)) #源数据是63 所以必须是63个
• 一维变多维
•  arr_1.reshape(9,7)
• arr_1.reshape(-1,7) #这-1 自适应行数，这里只能有一个参数是-1

4 级联

　　np.concatenate()

 　　1.一维，二维，多维数组的级联，实际操作中级联多为二维数组

　　　　如果是3维数组拼接axis=2

　　　　#np.concatenate((arr,arr）,axis=0) #行和行拼接
　　　　#np.concatenate((arr,arr),axis=1) #列和列拼接

　　图片操作

　　　　# imgs = np.concatenate((img_arr,img_arr),axis=0) #行
　　　　# imgs = np.concatenate((img_arr,img_arr),axis=1) #列
　　　　imgs1 = np.concatenate((img_arr,img_arr,img_arr),axis=1) #三列
　　　　imgs = np.concatenate((imgs1,imgs1,imgs1),axis=0) #九宫格画面
　　　　plt.imshow(imgs)

 　　3.np.hstack与np.vstack　　　

　　　　# np.hstack((arr,arr))#列拼接
　　　　# np.vstack((arr,arr)) #行拼接

级联需要注意的点：

• 级联的参数是列表：一定要加中括号或小括号
• 维度必须相同
• 形状相符:在维度保持一致的前提下，如果进行横向（axis=1）级联，必须保证进行级联的数组行数保持一致。如果进行纵向（axis=0）级联，必须保证进行级联的数组列数保持一致。
• 可通过axis参数改变级联的方向

5 切分

与级联类似，三个函数完成切分工作：

• np.split(arr,行／列号，轴):参数2是一个列表类型
• np.vsplit
• np.hsplit

 #图片切割实例

　　原图实例看上面

　　c1 =np.split(img_arr,[100,350],axis=0)[1] #切割列 取索引1
　　c2 = np.split(c1,[130,550],axis=1)[1] #切割行 取索引1
　　plt.imshow(c2) #最终效果是取中间小猫的脸部

6. 副本

所有赋值运算不会为ndarray的任何元素创建副本。对赋值后的对象的操作也对原来的对象生效

a = arr.copy() #创建副本
a[1,3] = 100000 #修改副本数值
a

ngarray 聚合的操作

　　　　1求和

　　　　arr.sum(axis=0)

　　　　arr.sun(axis=1)

　　　　最大值，最小值

　　　　　　# arr.max(axis=1)
　　　　　　# arr.min(axis=0)
　　　　　　np.min(arr)
　　　　　　np.max(arr)

　　　　3.平均值：np.mean()

　　　　　　

3. 其他聚合操作

Function Name    NaN-safe Version    Description
np.sum    np.nansum    Compute sum of elements
np.prod    np.nanprod    Compute product of elements
np.mean    np.nanmean    Compute mean of elements
np.std    np.nanstd    Compute standard deviation
np.var    np.nanvar    Compute variance
np.min    np.nanmin    Find minimum value
np.max    np.nanmax    Find maximum value
np.argmin    np.nanargmin    Find index of minimum value
np.argmax    np.nanargmax    Find index of maximum value
np.median    np.nanmedian    Compute median of elements
np.percentile    np.nanpercentile    Compute rank-based statistics of elements
np.any    N/A    Evaluate whether any elements are true
np.all    N/A    Evaluate whether all elements are true
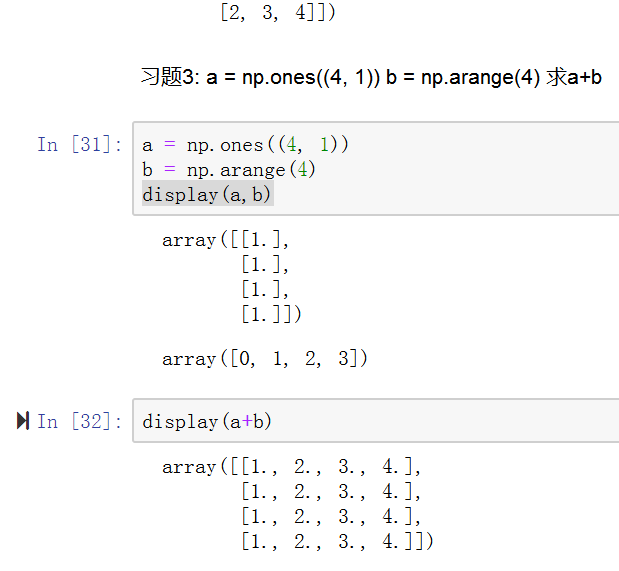
np.power 幂运算

五、广播机制

【重要】ndarray广播机制的三条规则:缺失维度的数组将维度补充为进行运算的数组的维度。缺失的数组元素使用已有元素进行补充。

• 规则一：为缺失的维度补1(进行运算的两个数组之间的维度只能相差一个维度)
• 规则二：缺失元素用已有值填充
• 规则三：缺失维度的数组只能有一行或者一列
• 
• 

  六、ndarray的排序

1. 快速排序

np.sort()与ndarray.sort()都可以，但有区别：

• np.sort()不改变输入
• ndarray.sort()本地处理，不占用空间，但改变输入

arr.sort()
arr

2. 部分排序

np.partition(a,k)

有的时候我们不是对全部数据感兴趣，我们可能只对最小或最大的一部分感兴趣。

• 当k为正时，我们想要得到最小的k个数
• 当k为负时，我们想要得到最大的k个数