目录
一.摘要
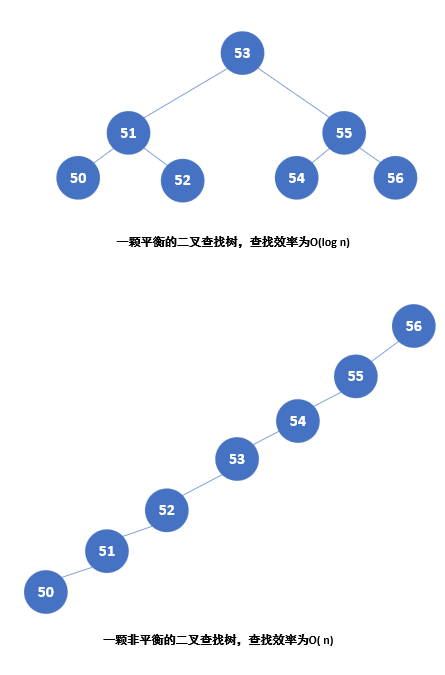
TreeMap是基于红黑树结构实现的一种Map,要分析TreeMap的实现首先就要对红黑树有所了解。红黑树是一种自平衡二叉查找树[1]。理论上,一颗平衡的二叉查找树的任意节点平均查找效率为树的高度h,即O(log n).但是如果二叉查找树失去平衡(元素全在一侧),搜索的效率就退化为O(n),因此二叉查找树的平衡是搜索效率的关键所在,而红黑树就是靠自平衡机制(红黑规则)来维持二叉查找树的平衡性。
【注1】:二叉查找树满足一下特点:
● 若左子树不为空,则左子树上所有节点的值均小于它的根节点的值;
● 若右子树不为空,则右子树上所有节点的值均大于它的根节点的值
● 左、右子树也分别为二叉查找树
● 没有键值相等的节点
二.红黑树
具体来说,红黑树是满足如下条件的二叉查找树(binary search tree):
1.每个节点要么是红色,要么是黑色。
2.根节点必须是黑色。
3.红色节点不能连续(也就是,红色节点的孩子和父亲都不能是红色)。
4.对于每个节点,从该点至null(树尾端)的任何路径,都含有相同个数的黑色节点。
5.每个叶节点(null)都是黑色的。
6.新加入到红黑树的节点为红色节点。
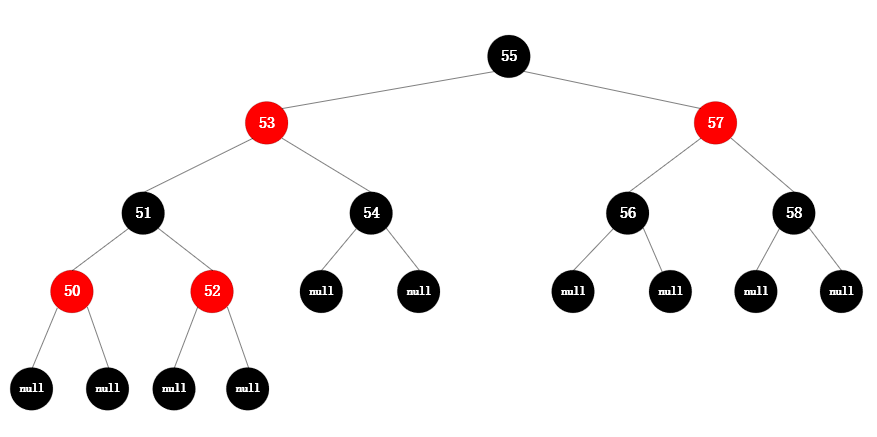
红黑树也是均衡二叉树,需要具备自动维持平衡的性质,上面的六条就是红黑树给出的自动维持平衡所需要具备的规则。典型的红黑树如下图所示:
红黑树的性质
☞ 从根节点到叶子结点的最长路径不大于最短路径的2倍
最短路径:纯由黑色节点组成的路径就是最短路径。
最长路径:根据规则3和规则4,若有红色节点,则必然有一个连接的黑色节点,当红色节点和黑色节点相同时,就是最长路径,也就是黑色节点(或红色节点)* 2。
☞ 新加入到红黑树的节点为红色节点
根据规则3,当前红黑树从根节点到每个叶子结点的黑色节点数量是一样的,此时加入新的节点是黑色节点的话,必然破坏规则,但加入红色节点却不一定,除非其父节点就是红色节点,因此加入红色节点,破坏规则的可能性小一些。三.红黑树的自平衡操作
3.1 红黑树插入元素后的自平衡操作
红黑树维持平衡主要通过两种方式【变色】和【旋转】,【旋转】又分【左旋】和【右旋】。红黑树的自平衡操作对应条件如下表所示:
| 无需调整 | 【变色】即可实现平衡 | 【旋转】+【变色】才可实现平衡 |
|---|---|---|
| 1.当父节点为黑色时插入子节点 | 2.空树插入根节点,将根节点红色变成黑色 | 4.父节点为红色左节点,叔父节点 [2] 为黑色,插入左子节点,通过【左左节点旋转】 |
| - | 3.父节点和叔父节点都为红色 | 5.父节点为红色左节点,叔父节点为黑色,插入右子节点,那么通过【左右节点旋转】 |
| - | - | 6.父节点为红色右节点,叔父节点为黑色,插入左子节点,那么通过【右左节点旋转】 |
| - | - | 7.父节点为红色右节点,叔父节点为黑色,插入右子节点,那么通过【右右节点旋转】 |
【注2】叔父节点指一个节点的父节点的兄弟节点
左旋:
逆时针旋转两个节点,让一个节点被其右子节点取代,而该节点成为右子节点的左子节点。
左旋操作步骤如下:
首先断开节点PL与右子节点G的关系,同时将其右子节点的引用指向节点C2;然后断开节点G与左子节点C2的关系,同时将G的左子节点的应用指向节点PL。

右旋:
顺时针旋转两个节点,让一个节点被其左子节点取代,而该节点成为左子节点的右子节点。
右旋操作步骤如下:
首先断开节点G与左子节点PL的关系,同时将其左子节点的引用指向节点C2;然后断开节点PL与右子节点C2的关系,同时将PL的右子节点的应用指向节点G。

3.1.1 当父节点为黑色时插入子节点
在左下图所示红黑树中插入59时,根据规则6,无须进行自平衡调整,结果如右下图所示:
 初始红黑树 初始红黑树 |
 添加59后的红黑树 添加59后的红黑树 |
3.1.2 空树插入根节点
根据规则2和规则6,需要将新插入红色节点变色为黑色的根节点。
3.1.3 父节点和叔父节点都为红色
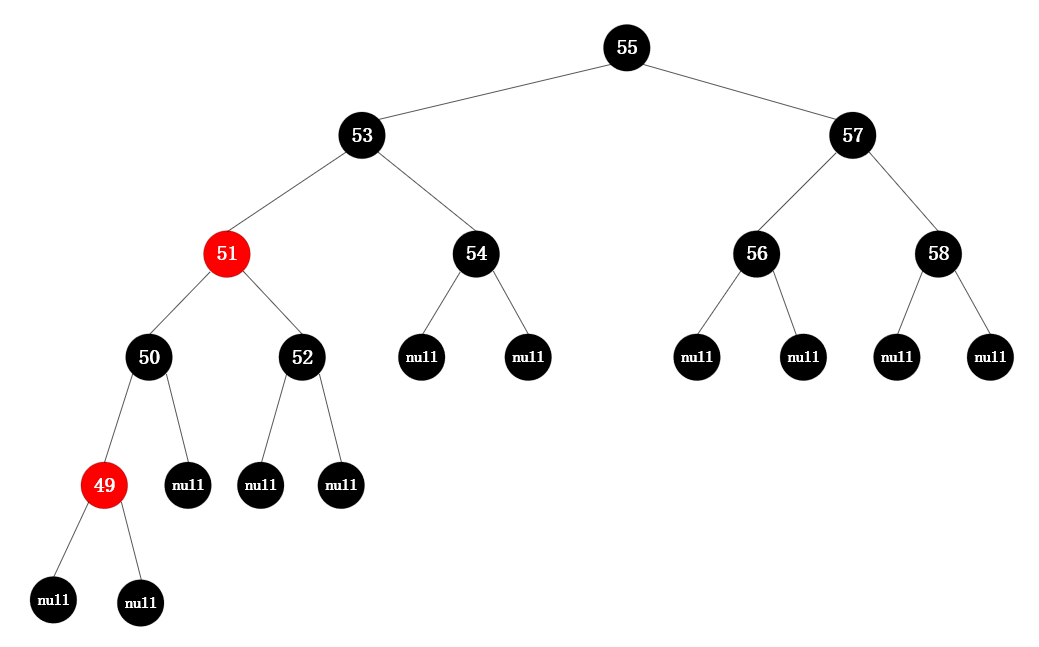
在左下图所示红黑树中插入49,根据规则6,结果如下图所示:
 初始红黑树 初始红黑树 |
 添加49后的红黑树 添加49后的红黑树 |

♦ 首先解决结构不遵守规则3(红色节点不能连续,节点50-49),需要将50改为黑色。
♦ 此时结构不遵守4(53-51-50-49-null路径上黑色节点个数为3,53-54-null路径上黑色节点个数为2),将51改为红色。
♦ 此时结构不遵守规则3(红色节点不能连续,节点53-51-52),将53改为黑色,52改为黑色。
♦ 此结构满足红黑树规则。
最终调整完成后的树为:
3.1.4 父节点为红色左节点,叔父节点为黑色,插入左子节点
旋转原始图如左下所示,在该树中插入65,规则: 以祖父节点【右旋】,搭配【变色】(左左节点旋转),自平衡过程如右下图所示:
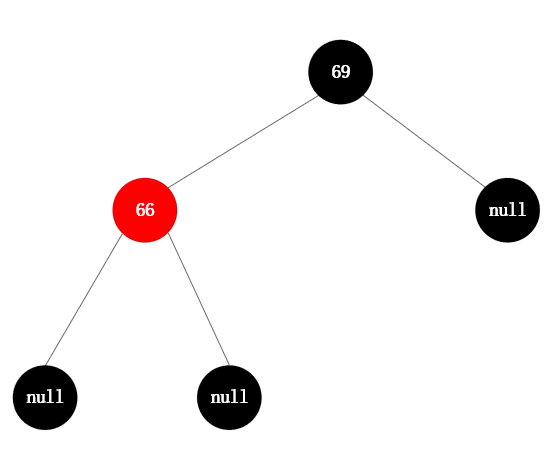 旋转原始图 旋转原始图 |
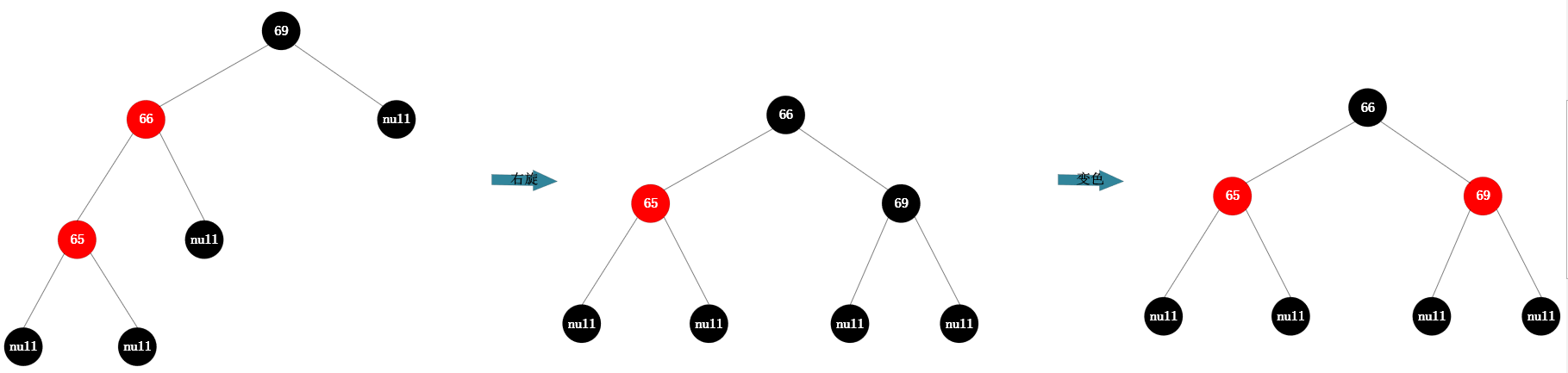 红黑树自平衡过程 红黑树自平衡过程 |
3.1.5 父节点为红色左节点,叔父节点为黑色,插入右子节点
旋转原始图如左下所示,在该树中插入67,规则: 先父节点【左旋】,然后祖父节点【右旋】,搭配【变色】(左右节点旋转),自平衡过程如右下图所示:
 旋转原始图 旋转原始图 |
 红黑树自平衡过程 红黑树自平衡过程 |
3.1.6 父节点为红色右节点,叔父节点为黑色,插入左子节点
旋转原始图如左下所示,在该树中插入68,规则: 先父节点【右旋】,然后祖父节点【左旋】,搭配【变色】(左右节点旋转),自平衡过程如右下图所示:
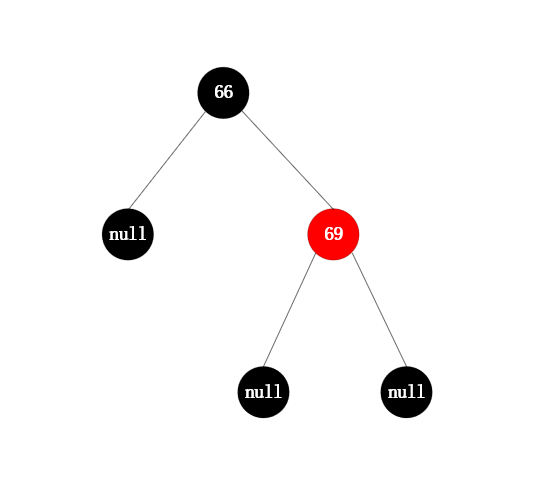 旋转原始图 旋转原始图 |
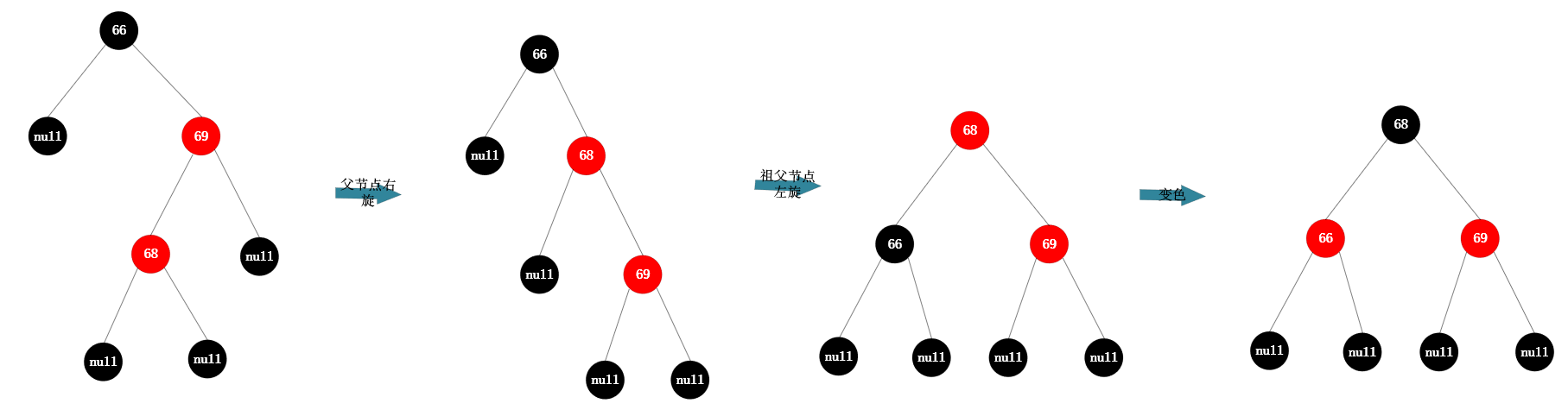 红黑树自平衡过程 红黑树自平衡过程 |
3.1.7 父节点为红色右节点,叔父节点为黑色,插入右子节点
旋转原始图如左下所示,在该树中插入70,规则: 先祖父节点【左旋】,搭配【变色】,自平衡过程如右下图所示:
 旋转原始图 旋转原始图 |
 红黑树自平衡过程 红黑树自平衡过程 |
3.2 红黑树删除元素后的自平衡操作
红黑树删除的情况比较多,存在以下情况:| 序号 | 条件 | 自平衡调节 |
|---|---|---|
| 1 | 删除的是根节点 | 直接将根节点置为null |
| 2 | 待删除节点的左右子节点都为null | 删除时将该节点置为null |
| 3 | 待删除节点的左右子节点有一个有值 | 用有值的节点替换该节点 |
| 4 | 待删除节点的左右子节点都不为null | 找前驱或者后继,将前驱或者后继的值复制到该节点中,然后删除前驱或者后继 |
3.2.1 删除的是根节点
直接将根节点置为null。
3.2.2 待删除节点的左右子节点都为null
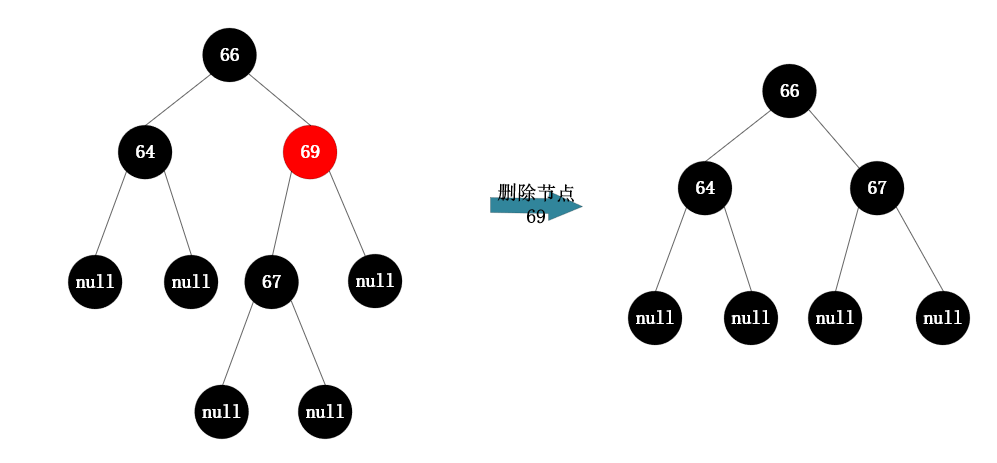
当待删除节点为红色子节点,且该节点左右子节点都为null,如下图所示:(待删除元素为红色子节点69)

当待删除节点为黑色子节点,且该节点左右子节点都是null,如下图所示:(待删除元素为黑色子节点67)
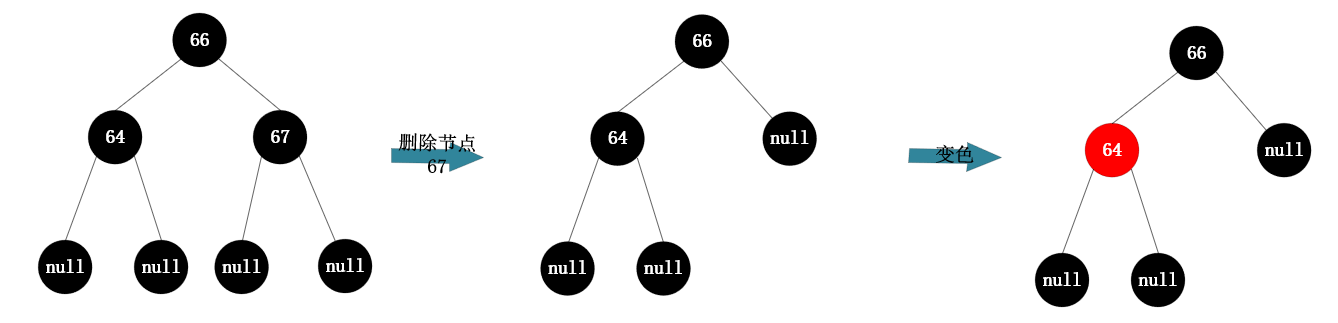
3.2.3 待删除节点的左右子节点有一个有值
当待删除节点的左右子节点有且仅有一个有值,将有用的节点替换该节点,如下图所示:(待删除元素为69)
3.2.4 待删除节点的左右子节点都是非null节点
第一步:找到该节点的前驱或者后继
前驱:左子树中值最大的节点(可得出其最多只有一个非null子节点,可能都为null);
后继:右子树中值最小的节点(可得出其最多只有一个非null子节点,可能都为null);
前驱和后继都是值最接近该节点值的节点。
第二步:将前驱或者后继的值复制到该节点中,然后删掉前驱或者后继
如果删除的是左节点,则将前驱的值复制到该节点中,然后删除前驱;如果删除的是右节点,则将后继的值复制到该节点中,然后删除后继;
1.使用前驱替换

分析:
因为要删除的是左节点64,找到该节点的前驱63;
然后用前驱的值63替换待删除节点的值64,此时两个节点(待删除节点和前驱)的值都为63;
删除前驱63,此时成为上图过程中间环节,但我们发现其不符合红黑树规则4,因此需要进行自动平衡调整;
这里直接通过【变色】即可完成。
2.使用后继替换

分析:
因为要删除的左节点64,找到该节点的后继节点65;
然后用后继的值65替换待删除节点的值64,此时两个节点(待删除节点和后继)的值都为65;
删除后继65,此时成为上图过程中间环节,但我们发现其不符合红黑树规则4,因此需要进行自动平衡调整;
四.方法分析
在TreeMap中,使用 fixAfterInsertion() 方法来实现插入后红黑树的自平衡操作;
使 fixAfterDeletion() 方法来实现删除后红黑树的自平衡操作。
fixAfterInsertion源码分析
private void fixAfterInsertion(Entry<K,V> x) {
//设置结点的初始化颜色为红色
x.color = RED;
//如果当前结点x不为null,并且不为根结点root,并且当前结点的父结点是红色结点,则进行循环
while (x != null && x != root && x.parent.color == RED) {
//如果当前结点x的父结点是x的祖结点的左结点
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
//获取结点x的叔叔结点y,也就是x祖结点的右结点
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
//如果叔结点y是红色
if (colorOf(y) == RED) {
//设置x的父结点为黑色
setColor(parentOf(x), BLACK);
//设置x的叔结点y为黑色
setColor(y, BLACK);
//设置x的祖结点为红色
setColor(parentOf(parentOf(x)), RED);
//设置祖结点为x
x = parentOf(parentOf(x));
//如果叔结点y是黑色
} else {
//判断当前结点x是否是父结点的右结点
if (x == rightOf(parentOf(x))) {
//x的父结点作为x
x = parentOf(x);
//将原来的父结点进行左旋操作
rotateLeft(x);
}
//设置x的父结点为黑色
setColor(parentOf(x), BLACK);
//设置x的祖结点为红色
setColor(parentOf(parentOf(x)), RED);
//x的祖结点进行右旋操作
rotateRight(parentOf(parentOf(x)));
}
//如果当前结点x的父结点是x的祖结点的右结点
} else {
//获取x结点的祖结点的左结点,也就是x的叔叔结点赋值给y
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
//如果叔结点y是红色的
if (colorOf(y) == RED) {
//设置x结点的父结点为黑色
setColor(parentOf(x), BLACK);
//设置x结点的叔结点y为黑色
setColor(y, BLACK);
//设置x的祖结点为红色
setColor(parentOf(parentOf(x)), RED);
//获取x结点祖结点赋值给x
x = parentOf(parentOf(x));
//如果叔结点y是黑色的
} else {
//如果x结点是x父结点的左结点
if (x == leftOf(parentOf(x))) {
//取x结点的父结点赋值为x
x = parentOf(x);
//将x结点右旋
rotateRight(x);
}
//设置x结点的父结点为黑色
setColor(parentOf(x), BLACK);
//设置x结点的祖结点为红色
setColor(parentOf(parentOf(x)), RED);
//将x结点的祖结点进行左旋
rotateLeft(parentOf(parentOf(x)));
}
}
}
//始终让根结点保持黑色,这是红黑树的特性
root.color = BLACK;
}
fixAfterDeletion源码分析
为注释方便,特做此规定:
N:当前待删除节点
P:N的父节点
S:N的兄弟节点,P的右子节点
Sl:S的左子节点
Sr:S的右子节点
对应关系如下图所示:

private void fixAfterDeletion(Entry<K,V> x) {
while (x != root && colorOf(x) == BLACK) { // N节点是黑色节点并且不是根节点就一直循环
if (x == leftOf(parentOf(x))) { // 如果N是P的左子节点
Entry<K,V> sib = rightOf(parentOf(x)); // sib就是N节点的兄弟节点S
if (colorOf(sib) == RED) { // 如果S节点是红色节点,满足删除冲突3.2,对P节点进行左旋操作并交换P和S的颜色
// 交换P和S的颜色,S原先为红色,P原先为黑色(2个红色节点不能相连)
setColor(sib, BLACK); // S节点从红色变成黑色
setColor(parentOf(x), RED); // P节点从黑色变成红色
rotateLeft(parentOf(x)); // 删除冲突3.2中P节点进行左旋
sib = rightOf(parentOf(x)); // 左旋之后N节点有了一个黑色的兄弟节点和红色的父亲节点,S节点重新赋值成N节点现在的兄弟节点。接下来按照删除冲突3.4、3.5、3.6处理
}
// 执行到这里S节点一定是黑色节点,如果是红色节点,会按照冲突3.2交换成黑色节点
// 如果S节点的左右子节点Sl、Sr均为黑色节点并且S节点也为黑色节点
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
// 按照删除冲突3.3和3.4进行处理
// 如果是冲突3.3,说明P节点也是黑色节点
// 如果是冲突3.4,说明P节点是红色节点,P节点和S节点需要交换颜色
// 3.3和3.4冲突的处理结果S节点都为红色节点,但是3.4冲突处理完毕之后直接结束,而3.3冲突处理完毕之后继续调整
setColor(sib, RED); // S节点变成红色节点,如果是3.4冲突需要交换颜色,N节点的颜色交换在跳出循环进行
x = parentOf(x); // N节点重新赋值成N节点的父节点P之后继续递归处理
} else { // S节点的2个子节点Sl,Sr中存在红色节点
if (colorOf(rightOf(sib)) == BLACK) { // 如果S节点的右子节点Sr为黑色节点,Sl为红色节点[Sl如果为黑色节点的话就在上一个if逻辑里处理了],满足删除冲突3.5
// 删除冲突3.5,对S节点做右旋操作,交换S和Sl的颜色,S变成红色节点,Sl变成黑色节点
setColor(leftOf(sib), BLACK); // Sl节点变成黑色节点
setColor(sib, RED); // S节点变成红色节点
rotateRight(sib); // S节点进行右旋操作
sib = rightOf(parentOf(x)); // S节点赋值现在N节点的兄弟节点
}
// 删除冲突3.5处理之后变成了删除冲突3.6或者一开始就是删除冲突3.6
// 删除冲突3.6,P节点做左旋操作,P节点和S接口交换颜色,Sr节点变成黑色
setColor(sib, colorOf(parentOf(x))); // S节点颜色变成P节点颜色,红色
setColor(parentOf(x), BLACK); // P节点变成S节点颜色,也就是黑色
setColor(rightOf(sib), BLACK); // Sr节点变成黑色
rotateLeft(parentOf(x)); // P节点做左旋操作
x = root; // 准备跳出循环
}
} else { // 如果N是P的右子节点,处理过程跟N是P的左子节点一样,左右对换即可
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK); // 删除冲突3.4循环调出来之后N节点颜色设置为黑色 或者 删除节点只有1个红色子节点的时候,将顶上来的红色节点设置为黑色
}
六.参考资料
面试常问:什么是红黑树?
关于红黑树(R-B tree)原理,看这篇如何
我的jdk源码(十九):TreeMap类 红黑树实现的map结构
红黑树之删除节点
红黑树旋转变色规则(最全面详细版)