内存地址对齐,是一种在计算机内存中排列数据、访问数据的一种方式,包含了两种相互独立又相互关联的部分:基本数据对齐和结构体数据对齐。当今的计算机在计算机内存中读写数据时都是按字(word)大小块来进行操作的(在32位系统中,数据总线宽度为32,每次能读取4字节,地址总线宽度为32,因此最大的寻址空间为2^32=4GB,但是最低2位A[0],A[1]是不用于寻址,A[2-31]才能存储器相连,因此只能访问4的倍数地址空间,但是总的寻址空间还是2^30*字长=4GB,因此在内存中所有存放的基本类型数据的首地址的最低两位都是0,除结构体中的成员变量)。基本类型数据对齐就是数据在内存中的偏移地址必须等于一个字的倍数,按这种存储数据的方式,可以提升系统在读取数据时的性能。为了对齐数据,可能必须在上一个数据结束和下一个数据开始的地方插入一些没有用处字节,这就是结构体数据对齐。
举个例子,假设计算机的字大小为4个字节,因此变量在内存中的首地址都是满足4地址对齐,CPU只能对4的倍数的地址进行读取,而每次能读取4个字节大小的数据。假设有一个整型的数据a的首地址不是4的倍数(如下图所示),不妨设为0X00FFFFF3,则该整型数据存储在地址范围为0X00FFFFF3~0X00FFFFF6的存储空间中,而CPU每次只能对4的倍数内存地址进行读取,因此想读取a的数据,CPU要分别在0X00FFFFF0和0X00FFFFF4进行两次内存读取,而且还要对两次读取的数据进行处理才能得到a的数据,而一个程序的瓶颈往往不是CPU的速度,而是取决于内存的带宽,因为CPU得处理速度要远大于从内存中读取数据的速度,因此减少对内存空间的访问是提高程序性能的关键。从上例可以看出,采取内存地址对齐策略是提高程序性能的关键。
举例:
首先我们先看看下面的C语言的结构体:
typedef struct MemAlign { int a; char b[3]; int c; }MemAlign;
以上这个结构体占用内存多少空间呢?也许你会说,这个简单,计算每个类型的大小,将它们相加就行了,以32为平台为例,int类型占4字节,char占用1字节,所以:4 + 3 + 4 = 11,那么这个结构体一共占用11字节空间。好吧,那么我们就用实践来证明是否正确,我们用sizeof运算符来求出这个结构体占用内存空间大小,sizeof(MemAlign),出乎意料的是,结果居然为12?看来我们错了?当然不是,而是这个结构体被优化了,这个优化有个另外一个名字叫“对齐”,那么这个对齐到底做了什么样的优化呢,听我慢慢解释,再解释之前我们先看一个图,图如下:

相信学过汇编的朋友都很熟悉这张图,这张图就是CPU与内存如何进行数据交换的模型,其中,左边蓝色的方框是CPU,右边绿色的方框是内存,内存上面的0~3是内存地址。这里我们这张图是以32位CPU作为代表,我们都知道,32位CPU是以双字(DWORD)为单位进行数据传输的,也正因为这点,造成了另外一个问题,那么这个问题是什么呢?这个问题就是,既然32位CPU以双字进行数据传输,那么,如果我们的数据只有8位或16位数据的时候,是不是CPU就按照我们数据的位数来进行数据传输呢?其答案是否定的,如果这样会使得CPU硬件变的更复杂,所以32位CPU传输数据无论是8位或16位都是以双字进行数据传输。那么也罢,8位或16位一样可以传输,但是,事情并非像我们想象的那么简单,比如,一个int类型4字节的数据如果放在上图内存地址1开始的位置,那么这个数据占用的内存地址为1~4,那么这个数据就被分为了2个部分,一个部分在地址0~3中,另外一部分在地址4~7中,又由于32位CPU以双字进行传输,所以,CPU会分2次进行读取,一次先读取地址0~3中内容,再一次读取地址4~7中数据,最后CPU提取并组合出正确的int类型数据,舍弃掉无关数据。那么反过来,如果我们把这个int类型4字节的数据放在上图从地址0开始的位置会怎样呢?读到这里,也许你明白了,CPU只要进行一次读取就可以得到这个int类型数据了。没错,就是这样,这次CPU只用了一个周期就得到了数据,由此可见,对内存数据的摆放是多么重要啊,摆放正确位置可以减少CPU的使用资源。
那么,内存对齐有哪些原则呢?我总结了一下大致分为三条:
第一条:第一个成员的首地址为0
第二条:每个成员的首地址是自身大小的整数倍
第二条补充:以4字节对齐为例,如果自身大小大于4字节,都以4字节整数倍为基准对齐。
第三条:最后以结构总体对齐。
第三条补充:以4字节对齐为例,取结构体中最大成员类型倍数,如果超过4字节,都以4字节整数倍为基准对齐。(其中这一条还有个名字叫:“补齐”,补齐的目的就是多个结构变量挨着摆放的时候也满足对齐的要求。)
上述的三原则听起来还是比较抽象,那么接下来我们通过一个例子来加深对内存对齐概念的理解,下面是一个结构体,我们动手算出下面结构体一共占用多少内存?假设我们以32位平台并且以4字节对齐方式:
#pragma pack(4) typedef struct MemAlign { char a[18]; double b; char c; int d; short e; }MemAlign;
下图为对齐后结构如下:
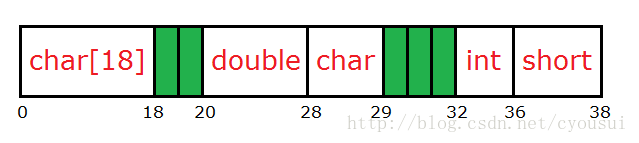
我们就以这个图来讲解是如何对齐的:
第一个成员(char a[18]):首先,假设我们把它放到内存开始地址为0的位置,由于第一个成员占18个字节,所以第一个成员占用内存地址范围为0~18。
第二个成员(double b):由于double类型占8字节,又因为8字节大于4字节,所以就以4字节对齐为基准。由于第一个成员结束地址为18,那么地址18并不是4的整数倍,我们需要再加2个字节,也就是从地址20开始摆放第二个成员。
第三个成员(char c):由于char类型占1字节,任意地址是1字节的整数倍,所以我们就直接将其摆放到紧接第二个成员之后即可。
第四个成员(int d):由于int类型占4字节,但是地址29并不是4的整数倍,所以我们需要再加3个字节,也就是从地址32开始摆放这个成员。
第五个成员(short e):由于short类型占2字节,地址36正好是2的整数倍,这样我们就可以直接摆放,无需填充字节,紧跟其后即可。
这样我们内存对齐就完成了。但是离成功还差那么一步,那是什么呢?对,是对整个结构体补齐,接下来我们就补齐整个结构体。那么,先让我们回顾一下补齐的原则:“以4字节对齐为例,取结构体中最大成员类型倍数,如果超过4字节,都以4字节整数倍为基准对齐。”在这个结构体中最大类型为double类型(占8字节),又由于8字节大于4字 节,所以我们还是以4字节补齐为基准,整个结构体结束地址为38,而地址38并不是4的整数倍,所以我们还需要加额外2个字节来填充结构体,如下图红色的就是补齐出来的空间:
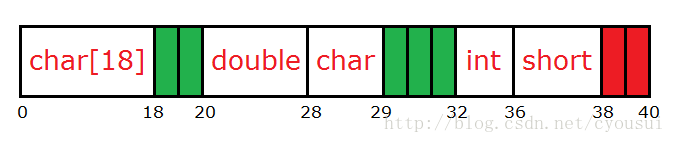
到此为止,我们内存对齐与补齐就完毕了!接下来我们用实验来证明真理,程序如下:
#include <stdio.h> #include <memory.h> // 由于VS2010默认是8字节对齐,我们 // 通过预编译来通知编译器我们以4字节对齐 #pragma pack(4) // 用于测试的结构体 typedef struct MemAlign { char a[18]; // 18 bytes double b; // 08 bytes char c; // 01 bytes int d; // 04 bytes short e; // 02 bytes }MemAlign; int main() { // 定义一个结构体变量 MemAlign m; // 定义个以指向结构体指针 MemAlign *p = &m; // 依次对各个成员进行填充,这样我们可以 // 动态观察内存变化情况 memset( &m.a, 0x11, sizeof(m.a) ); memset( &m.b, 0x22, sizeof(m.b) ); memset( &m.c, 0x33, sizeof(m.c) ); memset( &m.d, 0x44, sizeof(m.d) ); memset( &m.e, 0x55, sizeof(m.e) ); // 由于有补齐原因,所以我们需要对整个 // 结构体进行填充,补齐对齐剩下的字节 // 以便我们可以观察到变化 memset( &m, 0x66, sizeof(m) ); // 输出结构体大小 printf( "sizeof(MemAlign) = %d", sizeof(m) ); }
程序运行过程中,查看内存如下:
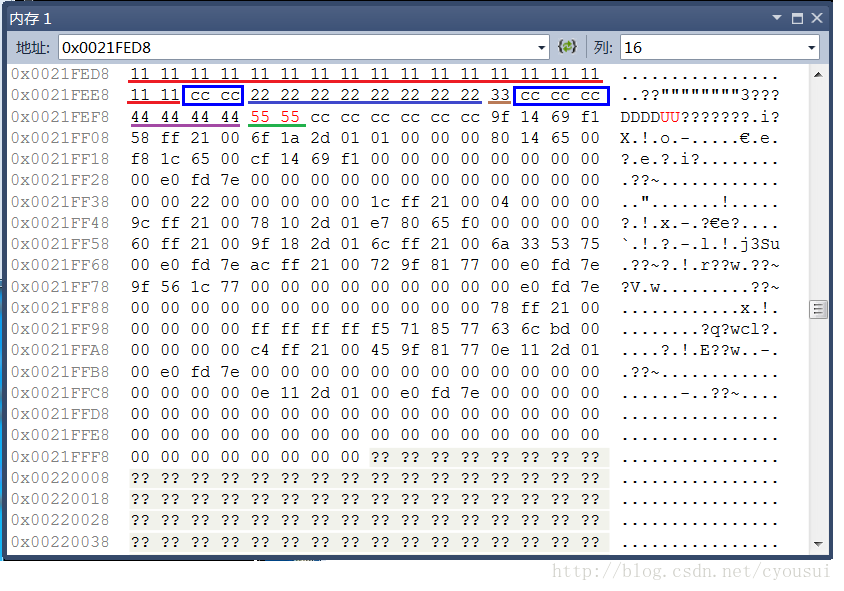
其中,各种颜色带下划线的代表各个成员变量,蓝色方框的代表为内存对齐时候填补的多余字节,由于这里看不到补齐效果,我们接下来看下图,下图篮框包围的字节就是与上图的交集以外的部分就是补齐所填充的字节。
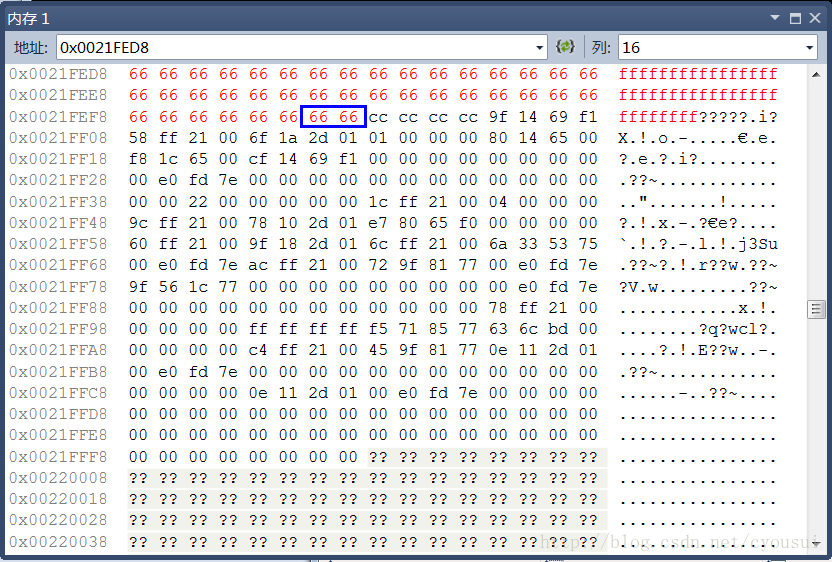
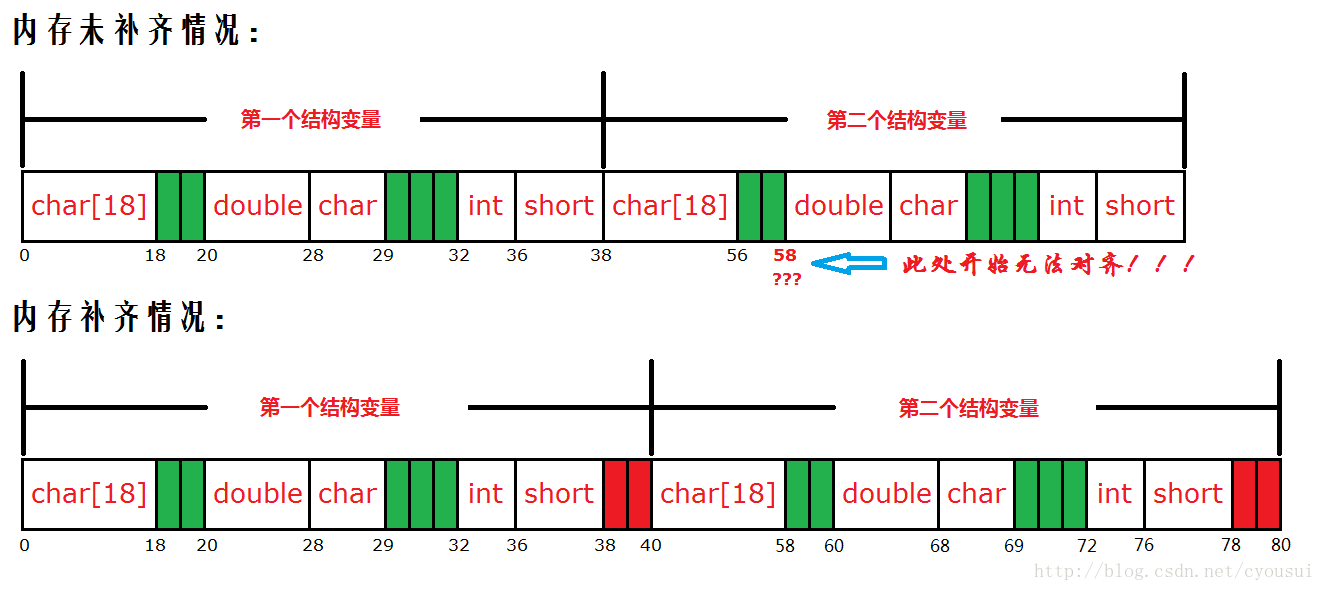
在最后,我在谈一谈关于补齐的作用,补齐其实就是为了让这个结构体定义的数组变量时候,数组内部,也同样满足内存对齐的要求,为了更好的理解这点,我做了一个跟本例子相对照的图:
参考链接:https://blog.csdn.net/donkeylong/article/details/4909720