题目:用面向对象的思维设计相关类,从而实现直线与直线、直线与圆、直线与矩形的交点。
菜鸡的C++实现:
公式:
直线与直线:ax+bx+c=0;
一般公式:X = (c * otherline.b - b* otherline.c)
/(b * otherline.a - a * otherline.b);
直线与圆:(x-x0)2 +(y-y0)2 =r2 此处用y=kx+b为直线k=-c/b,b=-c
c = -cirle.x0;d = -cirle.y0;
一般公式: x1=-(sqrt((k * k + 1) * cirle.r * cirle.r - c * c * k * k + (2 * c * d + 2 * b * c) * k - d * d - 2 * b * d - b * b) + (b + d) * k + c)
/ (k * k + 1);
x2= (sqrt((k * k + 1) * cirle.r * cirle.r - c * c * k * k + (2 * c * d + 2 * b * c) * k - d * d - 2 * b * d - b * b) - (b + d) * k - c)
/ (k * k + 1);
直线与矩形:考虑直线与四条直线在范围内是否有解即可
以下代码初步测试可用,若有bug谢谢指出
结构定义:graph.h
//圆
class Circle
{
public:
float r;
float x0;
float y0;
Circle(float r, float x0, float y0) {
this->r = r;
this->x0 = x0;
this->y0 = y0;
}
};
//矩形
class Rectangle {
public:
float topRightY;
float topRightx;
float bottomLeftY;
float bottomLeftX;
Rectangle(float topry, float toprx, float bottomly, float bottomlx) {
this->topRightx = toprx;
this->topRightY = topry;
this->bottomLeftX = bottomly;
this->bottomLeftY = bottomlx;
}
};
//直线
class Straight
{
public:
float a;
float b;
float c;
Straight(float a, float b, float c) {
this->a = a;
this->b = b;
this->c = c;
}
//求交点
void intersect(Straight otherline);
void intersect(Circle cirle);
void intersect(Rectangle rectangle);
};
算法实现graph.cpp
void Straight::intersect(Straight otherline)
{
if (this->b * otherline.a - this->a * otherline.b == 0)
{
if (this->c == otherline.c)
{
cout << "两直线重合,有无数交点" << endl;
return;
}
else
{
cout << "两直线平行无交点" << endl;
return;
}
}
else
{
float intersectX = (this->c * otherline.b - this->b * otherline.c) /
(this->b * otherline.a - this->a * otherline.b);
float intersectY= (this->a*otherline.c-this->c*otherline.a)/
(this->b * otherline.a - this->a * otherline.b);
cout << "两直线交点为:" << fixed << setprecision(2) << "(" <<
intersectX << "," <<intersectY<< ")"<<endl;
}
}
void Straight::intersect(Circle cirle)
{
float distanceR;
distanceR = abs(this->a * cirle.x0 + this->b * cirle.y0 + this->c) /
(sqrt(this->a * this->a + this->b * this->b));
cout << "直线与圆心距离:" << distanceR << endl;
if (distanceR > cirle.r)
cout << "该直线与圆无交点" << endl;
else if (this->a == 0) {
float x1, x2;
float y1, y2;
x1 = cirle.x0 + sqrt(cirle.r* cirle.r-(cirle.y0-this->c/this->b)*(cirle.y0 - this->c / this->b));
x2 = cirle.x0 -sqrt(cirle.r * cirle.r - (cirle.y0 - this->c / this->b) * (cirle.y0 - this->c / this->b));
y1 = y2 = -this->c / this->b;
if (x1 == x2)
cout << "直线与圆有一交点:(" << x1 << "," << y1 << ")" << endl;
else
cout << "直线与圆有两交点:(" << x1 << "," << y1 << ")" << ",(" << x2 << ", " << y2 << ")" << endl;
}
else if (this->b == 0) {
float x1, x2;
float y1, y2;
y1 = cirle.y0 + sqrt(cirle.r * cirle.r - (cirle.-x0 - this->c / this->a) * (cirle.x0 - this->c / this->a));
y2 = cirle.y0 - sqrt(cirle.r * cirle.r - (cirle.x0 - this->c / this->a) * (cirle.x0 - this->c / this->a));
x1 = x2 = -this->c / this->a;
if (y1 ==y2)
cout << "直线与圆有一交点:(" << x1 << "," << y1 << ")" << endl;
else
cout << "直线与圆有两交点:(" << x1 << "," << y1 << ")" << ",(" << x2 << ", " << y2 << ")" << endl;
}
else
{
float x1,x2;
float y1,y2;
float k = -this->a / this->b;
float b = -this->c / this->b;
float c = -cirle.x0;
float d = -cirle.y0;
x1=-(sqrt((k * k + 1) * cirle.r * cirle.r - c * c * k * k + (2 * c * d + 2 * b * c) * k - d * d - 2 * b * d - b * b) + (b + d) * k + c)
/ (k * k + 1);
x2= (sqrt((k * k + 1) * cirle.r * cirle.r - c * c * k * k + (2 * c * d + 2 * b * c) * k - d * d - 2 * b * d - b * b) - (b + d) * k - c)
/ (k * k + 1);
y1 = k*x1 + b;
y2 = k * x2 + b;
if (x1 == x2)
cout << "直线与圆有一交点:(" << x1 << "," << y1 << ")" << endl;
else
cout << "直线与圆有两交点:(" << x1 << "," << y1 << ")"<< ",(" << x2 << ", " << y2 << ")" << endl;
}
}
void Straight::intersect(Rectangle rectangle)
{
if (this->a == 0) {
if ((-this->c / this->b) == rectangle.bottomLeftY || (-this->c / this->b) == rectangle.topRightY)
{
cout << "直线与矩形一边重合,有无数交点" << endl;
return;
}
else if ((-this->c / this->b) < rectangle.bottomLeftY || (-this->c / this->b) > rectangle.topRightY)
{
cout << "直线与矩形无交点<<endl";
return;
}
else
{
cout << "直线与矩形两交点:("<<rectangle.bottomLeftX<<","<< (-this->c / this->b)<<"),(" << rectangle.topRightx << "," << (-this->c / this->b) << ")"<<endl;
return;
}
}
else if (this->b == 0) {
if ((-this->c / this->a) == rectangle.bottomLeftX || (-this->c / this->a) == rectangle.topRightx)
{
cout << "直线与矩形一边重合,有无数交点" << endl;
return;
}
else if ((-this->c / this->a) < rectangle.bottomLeftX || (-this->c / this->a) > rectangle.topRightx)
{
cout << "直线与矩形无交点<<endl";
return;
}
else
{
cout << "直线与矩形两交点:(" << -this->c / this->a << "," << rectangle.bottomLeftY << "),(" << -this->c / this->a << "," << rectangle.topRightY << ")" << endl;
return;
}
}
float X1, X2, X3, X4;
float Y1, Y2, Y3, Y4;
bool isHvae = false;
X1 = rectangle.bottomLeftX;
Y1 = -(this->a * X1 + this->c) / this->b;
X2 = rectangle.topRightx;
Y2 = -(this->a * X2 + this->c) / this->b;
Y3 = rectangle.bottomLeftY;
X3 = -(this->b * Y3 + this->c) / this->a;
Y4 = rectangle.topRightY;
X4 = -(this->b * Y4 + this->c) / this->a;
if (Y1 <= rectangle.topRightY && Y1 >= rectangle.bottomLeftY)
{
cout << "存在交点:(" <<X1 <<","<<Y1<<")";
isHvae = true;
}
if (Y2 <= rectangle.topRightY && Y2 >= rectangle.bottomLeftY)
{
cout << "存在交点:(" << X2 << "," << Y2 << ")";
isHvae = true;
}
if (X3 < rectangle.topRightx && X3 > rectangle.bottomLeftX)
{
cout << "存在交点:(" << X3 << "," << Y3 << ")";
isHvae = true;
}if (X4 < rectangle.topRightx && X4 > rectangle.bottomLeftX)
{
cout << "存在交点:(" << X4 << "," << Y4 << ")";
isHvae = true;
}
if(!isHvae)
cout << "无交点" << endl;
cout << endl;
}
main
int main() {
Straight straight(1, 1, -1);
Straight otherStraight(-1, 1, 0);
Rectangle rectangle(2, 2,1,-1);
Circle circle(0.5, 0.5, 0.5);
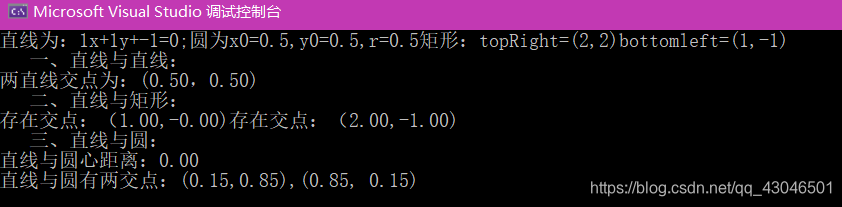
cout << "直线为:" << straight.a << "x+" << straight.b << "y+" << straight.c <<"=0;"
<< "圆为x0="<<circle.x0<<",y0="<<circle.y0<<",r="<<circle.r
<<"矩形:topRight=("<<rectangle.topRightx<<","<<rectangle.topRightY<<")bottomleft=("<<rectangle.bottomLeftX << "," << rectangle.bottomLeftY << ")"<<endl;
cout<<"直线与直线:" << endl;
straight.intersect(otherStraight);
cout << "直线与矩形:" << endl;
straight.intersect(rectangle);
cout << "直线与圆:" << endl;
straight.intersect(circle);
}