主题链接:http://acm.hdu.edu.cn/showproblem.php?pid=2454
Problem Description
Wang Haiyang is a strong and optimistic Chinese youngster. Although born and brought up in the northern inland city Harbin, he has deep love and yearns for the boundless oceans. After graduation, he came to a coastal city and got a job in a marine transportation
company. There, he held a position as a navigator in a freighter and began his new life.
The cargo vessel, Wang Haiyang worked on, sails among 6 ports between which exist 9 routes. At the first sight of his navigation chart, the 6 ports and 9 routes on it reminded him of Graph Theory that he studied in class at university. In the way that Leonhard Euler solved The Seven Bridges of Knoigsberg, Wang Haiyang regarded the navigation chart as a graph of Graph Theory. He considered the 6 ports as 6 nodes and 9 routes as 9 edges of the graph. The graph is illustrated as below.
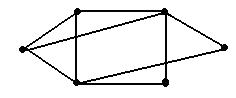
According to Graph Theory, the number of edges related to a node is defined as Degree number of this node.
Wang Haiyang looked at the graph and thought, If arranged, the Degree numbers of all nodes of graph G can form such a sequence: 4, 4, 3,3,2,2, which is called the degree sequence of the graph. Of course, the degree sequence of any simple graph (according to Graph Theory, a graph without any parallel edge or ring is a simple graph) is a non-negative integer sequence?
Wang Haiyang is a thoughtful person and tends to think deeply over any scientific problem that grabs his interest. So as usual, he also gave this problem further thought, As we know, any a simple graph always corresponds with a non-negative integer sequence. But whether a non-negative integer sequence always corresponds with the degree sequence of a simple graph? That is, if given a non-negative integer sequence, are we sure that we can draw a simple graph according to it.?
Let's put forward such a definition: provided that a non-negative integer sequence is the degree sequence of a graph without any parallel edge or ring, that is, a simple graph, the sequence is draw-possible, otherwise, non-draw-possible. Now the problem faced with Wang Haiyang is how to test whether a non-negative integer sequence is draw-possible or not. Since Wang Haiyang hasn't studied Algorithm Design course, it is difficult for him to solve such a problem. Can you help him?
The cargo vessel, Wang Haiyang worked on, sails among 6 ports between which exist 9 routes. At the first sight of his navigation chart, the 6 ports and 9 routes on it reminded him of Graph Theory that he studied in class at university. In the way that Leonhard Euler solved The Seven Bridges of Knoigsberg, Wang Haiyang regarded the navigation chart as a graph of Graph Theory. He considered the 6 ports as 6 nodes and 9 routes as 9 edges of the graph. The graph is illustrated as below.

According to Graph Theory, the number of edges related to a node is defined as Degree number of this node.
Wang Haiyang looked at the graph and thought, If arranged, the Degree numbers of all nodes of graph G can form such a sequence: 4, 4, 3,3,2,2, which is called the degree sequence of the graph. Of course, the degree sequence of any simple graph (according to Graph Theory, a graph without any parallel edge or ring is a simple graph) is a non-negative integer sequence?
Wang Haiyang is a thoughtful person and tends to think deeply over any scientific problem that grabs his interest. So as usual, he also gave this problem further thought, As we know, any a simple graph always corresponds with a non-negative integer sequence. But whether a non-negative integer sequence always corresponds with the degree sequence of a simple graph? That is, if given a non-negative integer sequence, are we sure that we can draw a simple graph according to it.?
Let's put forward such a definition: provided that a non-negative integer sequence is the degree sequence of a graph without any parallel edge or ring, that is, a simple graph, the sequence is draw-possible, otherwise, non-draw-possible. Now the problem faced with Wang Haiyang is how to test whether a non-negative integer sequence is draw-possible or not. Since Wang Haiyang hasn't studied Algorithm Design course, it is difficult for him to solve such a problem. Can you help him?
Input
The first line of input contains an integer T, indicates the number of test cases. In each case, there are n+1 numbers; first is an integer n (n<1000), which indicates there are n integers in the sequence; then follow n integers, which indicate the numbers
of the degree sequence.
Output
For each case, the answer should be "yes"or "no" indicating this case is "draw-possible" or "non-draw-possible"
Sample Input
2 6 4 4 3 3 2 2 4 2 1 1 1
Sample Output
yes no
Source
题意:
给出一个图的每个点的度数,求是否能构成一个简单图。
PS:
Havel定理:http://baike.baidu.com/view/8698382.htm?
fr=aladdin
给定一个非负整数序列{dn},若存在一个无向图使得图中各点的度与此序列一一相应,则称此序列可图化。进一步。若图为简单图,则称此序列可简单图化
可图化的判定:d1+d2+……dn=0(mod 2)。
关于详细图的构造,我们能够简单地把奇数度的点配对,剩下的所有搞成自环。
可简单图化的判定(Havel定理):把序列排成不增序,即d1>=d2>=……>=dn,则d可简单图化当且仅当d’={d2-1,d3-1。……d(d1+1)-1, d(d1+2)。d(d1+3),……dn}可简单图化。简单的说,把d排序后,找出度最大的点(设度为d1),把它与度次大的d1个点之间连边,然后这个点就能够无论了。一直继续这个过程。直到建出完整的图。或出现负度等明显不合理的情况。
代码例如以下:
#include<cstdio>
#include<algorithm>
using namespace std;
bool cmp(int a,int b)
{
return a>b;
}
int main()
{
int t,n,i,j;
int a[1010];
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
int sum = 0;
for(i=0; i<n; i++)
{
scanf("%d",&a[i]);
sum+=a[i];
}
if(sum%2)
{
printf("no
");
continue;
}
for(i=0; i<n; i++)
{
if(a[i]>=n)
break;
}
if(i<n)
{
printf("no
");
continue;
}
int flag = 0;
for(i=0; i<n; i++)
{
int cnt=0;
sort(a,a+n,cmp);
for(j=1; j<n; j++)
{
if(cnt==a[0])
break;
a[j]--;
cnt++;
if(a[j] < 0)
{
flag = 1;
break;
}
}
if(flag)
break;
if(cnt==0)
break;
a[0]-=cnt;
}
for(i=0; i<n; i++)
{
//printf("%d ",a[i]);
if(a[i])
break;
}
//printf("
");
if(i<n || flag)
printf("no
");
else
printf("yes
");
}
return 0;
}
/*
4
4 3 2 1 1
*/
版权声明:本文博客原创文章,博客,未经同意,不得转载。